
- •Введение
- •Раздел I. МЕТОДЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
- •1. Приближенное решение уравнения
- •2. Метод последовательных приближений решения уравнения
- •3. Метод Ньютона (метод касательных) решения уравнения
- •4. Метод секущих (метод хорд) решения уравнения
- •8. Приближенные вычисления значений функций с помощью рядов
- •9. Приближенные вычисления пределов с помощью рядов
- •10. Задачи для самостоятельного решения
- •Раздел II. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- •1. Квадратурные формулы
- •3. Формула трапеций
- •4. Метод парабол (метод Симпсона)
- •5. Вычисление определенных интегралов с помощью рядов
- •6. Задачи для самостоятельного решения
- •Раздел III. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •1. Метод Пикара последовательных приближений
- •2. Метод Эйлера
- •3. Улучшенный метод Эйлера
- •4. Метод Эйлера–Коши
- •5. Метод Рунге–Кутта
- •6. Метод Адамса
- •8. Метод конечных разностей решения краевых задач для обыкновенных дифференциальных уравнений
- •10. Метод наименьших квадратов
- •11. Задачи для самостоятельного решения
- •Раздел IV. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ ГИПЕРБОЛИЧЕСКОГО ТИПА
- •1. Виды уравнений математической физики
- •2. Вывод уравнения колебания струны
- •7. Задачи для самостоятельного решения
- •Раздел V. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ ПАРАБОЛИЧЕСКОГО ТИПА
- •4. Распространение тепла в неограниченном стержне
- •6. Задачи для самостоятельного решения
- •Раздел VI. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ ЭЛЛИПТИЧЕСКОГО ТИПА
- •1. Уравнения эллиптического типа и краевые задачи для них
- •3. Уравнение Лапласа в цилиндрических координатах
- •5. Примеры решения задач
- •6. Задачи для самостоятельного решения
- •Раздел VII. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- •1. Метод сеток численного решения дифференциальных уравнений с частными производными
- •3. Метод сеток для уравнения гиперболического типа
- •5. Метод прогонки для уравнения теплопроводности
- •6. Решение уравнения движения грунта
- •7. Задачи для самостоятельного решения
- •Раздел VIII. ВАРИАЦИОННЫЕ МЕТОДЫ
- •1. Некоторые сведения из функционального анализа
- •2. Теоретические основы метода Ритца
- •5. Задачи для самостоятельного решения
- •Раздел IX. КОРРЕЛЯЦИЯ
- •1. Понятие корреляции
- •4. Корреляция
- •5. Задачи для самостоятельного решения
- •Библиографический список
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
sin |
|
|
|
|
xn 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
xn 1 |
|
|
||||||||||
xn xn 1 |
|
|
|
|
180 |
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
cos |
|
|
|
xn 1 |
|
|
|
|
|
|||||
|
|
180 |
|
|
|
x2 |
|
|
||||||||||
|
|
|
|
180 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
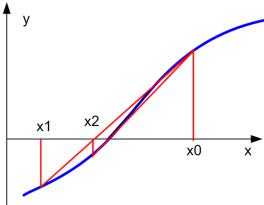
СиГрафическаябАинтерпретация методаДхорд представленаИна рис. 3.
|
4. Метод секущих (метод хорд) решения уравнения |
|
||||||||||||
|
Пусть функц я y f x непрерывна на отрезке [ xn 1 |
, xn 2 ], где |
||||||||||||
xn 1 , |
xn 2 – пр |
бл женные значения корня уравнения f x 0 , и вы- |
||||||||||||
полняется услов е f xn 1 f xn 2 0. |
|
|
точки xn 1 ; f xn 1 |
|||||||||||
|
Проведем |
хорду, |
соединяющую |
|
||||||||||
xn 2 |
; f xn 2 . Уравнение хорды |
|
|
|
|
|
|
|
|
|
||||
|
|
|
y f xn 2 |
|
|
x |
x xn 2 |
. |
|
|||||
|
|
|
f x |
n 1 |
f x |
|
|
n 1 |
x |
n 2 |
|
|||
|
|
|
|
n 2 |
|
|
|
|
|
|||||
|
Найдем координату пересечения хорды с осью Оx: |
|
||||||||||||
|
xn xn 1 |
f xn 1 |
|
xn 1 xn 2 . |
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
f xn 1 f xn 2 |
|
|
|
|
|
|||||
|
Получили рекуррентное соотношение для нахождения корня |
|||||||||||||
уравнения f x |
0 методом хорд. |
|
|
|
|
|
|
|
|
|||||
Рис. 3
10
Точка xn делит отрезок [ xn 1 , xn 2 ] на два. Выбираем тот отрезок, на концах которого функция y f x принимает разные знаки.
Процесс продолжаем до тех пор, пока не будет достигнута требуемая точность вычисления.
Методом хорд называют также метод, при котором один из кон-
цов отрезка закреплен, то есть вычисление приближения корня урав- |
||||||||||||||||||||
СибАДИ |
||||||||||||||||||||
нения f x 0 |
производят по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
xn xn 1 |
|
f |
|
xn 1 |
|
xn 1 x0 . |
|
||||||||||||
|
|
|
f xn 1 f x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
Пр мер. |
Для уравнения |
|
f x sin |
|
|
|
|
|
x |
|
|
|
0 рекуррент- |
|||||||
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
x |
|
||||
ные формулы пр л жения решения методом хорд имеют вид |
||||||||||||||||||||
|
|
sin xn 1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
xn xn 1 |
|
|
|
|
|
|
xn 1 |
|
|
|
|
|
|
|
|
|
xn 1 xn 2 . |
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
xn 2 |
|
|
|
|
|
|
|
|||||||||
|
sin xn 1 |
|
|
|
f |
|
|
|
|
|
|
|
|
|||||||
|
|
|
xn 1 |
|
|
|
|
|
xn 2 |
|
|
|
||||||||
В отличие от двух рассмотренных выше методов метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.
5. Метод половинного деления (метод дихотомии) решения
уравнения |
|
|
|
|
|
Пусть |
функция y f x |
непрерывна на отрезке [ x0 , x1 ]. |
Ес- |
||
ли x0 , x1 – приближенные значения корня уравнения |
f x 0 |
вы- |
|||
полняется |
условие f x0 f x1 0, то последующие |
приближения |
|||
находится по формуле |
|
|
|
|
|
|
xn 2 |
|
xn xn 1 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
11
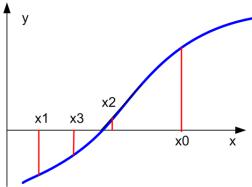
и вычисляется f xn 2 . Если f xn 2 0 , то корень найден. В противном случае из отрезков выбирается тот, на концах которого f x
принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.
Геометрическая интерпретация метода дихотомии показана на
рис. 4. |
|
|
|
|
|
|
СибАДИ |
||||||
|
|
|
|
Рис. 4 |
|
|
6. Приближенные вычисления с помощью дифференциала |
||||||
значений функции одной переменной |
|
|
||||
Пусть функция |
y f (x) имеет в точке x отличную от нуля про- |
|||||
изводную |
lim |
y |
|
|
|
|
x |
y x 0 . Тогда стоящее под пределом отноше- |
|||||
|
x 0 |
|
|
|
|
|
y |
|
|
|
y |
|
|
ние x можно |
представить в виде суммы x y x x , где |
|||||
x является |
бесконечно малой величиной при |
x 0 , |
то есть |
|||
lim x 0 . |
Это означает, что приращение функции y |
можно |
||||
x 0 |
|
|
|
|
|
|
представить в виде |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y y x x x x . |
|
|
Таким образом, |
приращение функции y представляет собой |
|||||
сумму двух слагаемых. При этом первое слагаемое является бесконечно малой величиной одного порядка малости с приращением ар-
12

гумента x . Второе слагаемое является бесконечно малой величиной более высокого порядка в сравнении с приращением аргумента x .
Главная линейная часть приращения y y x x x x , то есть слагаемое y x x называется дифференциалом функции y f (x) и обозначается dy : dy= y x x .
СибАДИ |
|||||||||||||||||||||||
|
|
Поскольку приращение аргумента равно дифференциалу аргу- |
|||||||||||||||||||||
мента dx= x , дифференциал функции одной переменной можно за- |
|||||||||||||||||||||||
писать в в |
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy= y x d x . |
|
|
|
|
|
|
|||||||
|
|
Если пр ращен е аргумента x мало по абсолютной величине, |
|||||||||||||||||||||
то dy y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
мы получаем y y x x y x d y y x x |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
y x0 x y x0 |
|
|
|
|
|
|
|
|
(1) |
||||||
|
|
|
|
|
|
|
|
y |
x0 x . |
||||||||||||||
|
|
Это |
формула |
при лиженного вычисления значения функции |
|||||||||||||||||||
y f (x) |
в точке x0 |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Примеры. 1. Покажем, как производятся приближенные вычис- |
|||||||||||||||||||||
ления на примере вычисления 4 620 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Решение. |
Вычислять 4 620 будем по формуле (1). Рассмотрим |
||||||||||||||||||||
функцию y 4 |
x при x 620 625 5. То есть |
x 625 ; |
x 5 . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Находим y x y 625 4 625 5. Вычисляем производную: |
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
x |
|
|
; |
y 625 |
|
|
|
|
|
|
|
. |
Теперь |
подставляем |
|||||||
|
44 x3 |
44 6253 |
|
4 125 |
|||||||||||||||||||
найденные значения в формулу (1): |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
4 620 5 |
|
1 |
|
|
5 5 0,01 4,99. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
4 |
125 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
Итак, 4 620 4,99. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2. Теперь по формуле (1) вычислим приближенно sin 183o . |
|||||||||||||||||||||
|
|
Решение. |
Используем |
|
|
функцию |
|
y sin x при |
x 183o |
||||||||||||||
180o 3o. То есть |
x 180o ; |
x 3o |
|
|
|
|
|
3 . |
|
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
180 |
|
|
60 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
13
Находим y x |
|
sin 180o 0. |
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
||
Вычисляем |
|
производную: |
y |
sin x cos x ; |
|
||||||
|
|
y 180 |
|
||||||||
cos180o 1. Теперь используем формулу (1): |
|
|
|
||||||||
|
|
sin 183o |
0 |
|
1 0,052. |
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
СибАДИ |
|||||||||||
|
|
|
|
60 |
|
|
|
|
|
|
|
Получ ли sin 183o 0,052. |
|
|
|
|
|
|
|
|
|||
7. Пр бл женные вычисления с помощью дифференциала |
|
||||||||||
значен й функц |
|
нескольких переменных |
|
|
|
||||||
По аналог |
с л неаризацией функции одной переменной мож- |
||||||||||
но при пр бл женном вычислении значений функции нескольких пе- |
|||||||||||
ременных, д фференц руемой в некоторой точке, заменять ее прира- |
|||||||||||
щение д фференц алом. |
|
|
|
|
|
|
|
|
|
||
Полный дифференциал функции |
z f (x1, x2 ,..., xn ) |
n перемен- |
|||||||||
ных имеет вид |
|
|
|
|
|
|
|
|
|
|
|
dz fx1 d x1 |
fx2 |
dx2 ... fxn dxn . |
|
|
|
||||||
Поскольку dz z ; dxi |
xi |
при i 1, 2,..., n, получаем форму- |
|||||||||
лу для приближенных вычислений |
|
|
|
|
|
|
|
||||
z fx1 x1 |
fx2 |
x2 |
|
... fxn xn . |
|
|
|
||||
В частности, для функции двух переменных z f (x, y) формула приближенных вычислений с помощью дифференциала имеет вид
z fx x0 , y0 x f y x0 , y0 y ,
или
|
|
x0 ; y0 |
y . |
(2) |
z x0 x; y0 y z x0 ; y0 fx |
x0 ; y0 x f y |
14
