
- •Оглавление
- •Предисловие
- •§ 1. Гармонические колебания
- •§ 2. Затухающие колебания
- •§ 3. Вынужденные колебания. Резонанс
- •§ 4. Векторная диаграмма напряжений
- •§ 5. Связь добротности с формой резонансных кривых
- •§ 6. Переменный ток
- •§ 7. Вынужденные колебания в параллельном контуре
- •§ 8. Метод комплексных амплитуд
- •Задачи
- •§ 9. Волновое уравнение и его решения
- •§ 10. Скорость и энергия упругих волн в твердой среде
- •§ 11. Перенос энергии упругой волной
- •§ 12. Стоячая волна
- •§ 13. Характеристики звука. Эффект Доплера для звуковых волн
- •Задачи
- •§ 14. Векторное волновое уравнение для электромагнитного поля
- •§ 15. Плоская электромагнитная волна и ее свойства
- •§ 16. Энергия электромагнитных волн
- •§ 17. Импульс и давление электромагнитного поля
- •§ 18. Дипольное излучение
- •Задачи
- •§ 19. Свойства световой волны. Законы отражения и преломления
- •§ 20. Формулы Френеля. Закон Брюстера
- •§ 21. Фотометрические величины и единицы
- •§ 22. Законы геометрической оптики. Принцип Ферма
- •§ 23. Увеличение оптических приборов, вооружающих глаз
- •Задачи
- •§ 24. Интерференция световых волн от двух когерентных источников
- •§ 25. Интерференция двух плоских волн
- •§ 27. Фурье-спектр световой волны
- •§ 28. Пространственная когерентность
- •§ 29. Интерференция в тонких пластинках
- •§ 30. Интерференционный опыт с бипризмой Френеля
- •Задачи
- •§ 33. Дифракция Френеля от щели
- •§ 34. Дифракция Фраунгофера от щели
- •§ 35. Количественный критерий вида дифракции
- •§ 36. Многолучевая интерференция
- •§ 37. Дифракционная решетка
- •§ 38. Дифракционная решетка как спектральный прибор
- •§ 39. Разрешающая сила объектива и оптимальное увеличение зрительной трубы
- •Задачи
- •§ 40. Поляризованный и естественный свет. Закон Малюса
- •§ 41. Поляризация света при отражении и преломлении
- •§ 42. Двойное лучепреломление
- •§ 43. Вращение плоскости поляризации
- •Задачи
- •§ 44. Дисперсия света. Групповая скорость
- •§ 45. Элементарная теория дисперсии
- •§ 46. Поглощение и рассеяние света
- •Задачи
- •Ответы к задачам
- •Приложения
- •Электрические колебания
- •Гармонические колебания
- •Затухающие колебания
- •Вынужденные колебания
- •Упругие волны
- •Электромагнитные волны
- •Свойства световой волны
- •Фотометрия
- •Интерференция света
- •Когерентность
- •Дифракция света
- •Поляризация света
- •Дисперсия света
- •II. Производные единицы СИ электрических, магнитных и световых величин
- •III. Постоянные некоторых веществ
- •Предметный указатель

104 |
Введение в оптику |
[ Гл. IV |
Светимость. |
Фотометрическая величина, |
называемая светимо- |
стью, является характеристикой протяженного источника света. Светимость M источника равна световому потоку, испускаемому
единицей площади поверхности источника по всем направлениям в телесный угол 2π стерадиан. Количественное  определение светимости M таково:
определение светимости M таково:
M = dΦdSисп ,
где dΦисп — световой поток, испускаемый эле-
ментом поверхности источника площади dS по всем направлениям в телесный угол 2π стерадиан (рис. 67).
Единица светимости — люмен на квадратный метр (лм/м2).
П р и м е р. Вычислим светимость M ламбертовского |
излучателя, |
яркость которого равна L. |
|
Световой поток dΦ, посылаемый участком поверхности |
S излуча- |
теля в элементарный телесный угол dΩ = sin θ dθ dϕ, равен dΦ = LdΩΔS cos θ = L sin θ dθ dϕ S cos θ.
Здесь θ и ϕ — сферические координаты (полярный и азимутальный углы), определяющие направление излучения (положение в пространстве элементарного телесного угла dΩ); полярный угол θ является углом между нормалью к излучающей поверхности и направлением излучения.
Световой поток , излучаемый по всем направлениям в телесный угол 2π стерадиан, вычисляется интегрированием по углу θ в пределах от нуля до π/2 и по углу ϕ в пределах от нуля до 2π:
θ= π2 ϕ=2π
=
L S sin θ cos θ dθ dϕ = πL S.
θ=0 ϕ=0
Отсюда светимость ламбертовского источника
M =
S
= πL.
§ 22. Законы геометрической оптики. Принцип Ферма
Геометрической (лучевой) оптикой называется раздел оптики, в котором не принимается во внимание волновая природа света. Законы геометрической оптики выполняются, если длина световой волны пренебрежимо мала по сравнению с характерными размерами неоднородностей среды, в которой распространяется свет. Основные законы геометрической оптики могут быть сформулированы следующим образом.
§ 22 ] |
Законы геометрической оптики. Принцип Ферма |
105 |
1.В однородной среде свет распространяется прямолинейно (световые лучи представляют собой прямые линии).
2.Световые лучи, пересекаясь, не возмущают друг друга; в частности, не изменяется направление распространения лучей.
3.При пересечении границы раздела двух сред падающий, отраженный и преломленный лучи лежат в одной плоскости (плоскости падения); угол падения равен углу отражения.
4.Угол падения θ1 и угол преломления θ2 связаны законом преломления n1 sin θ1 = n2 sin θ2, где n1 и n2 — абсолютные показатели преломления сред.
В основе геометрической оптики лежит принцип Ферма: свет распространяется по такому пути, для прохождения которого ему требуется минимальное время или оптическая длина пути которого минимальна.
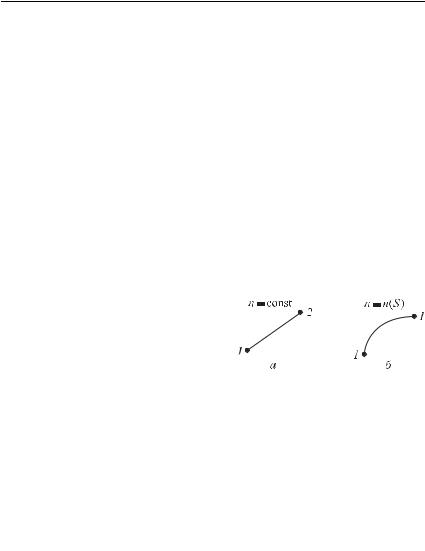
Определим понятие оптической длины пути и покажем, что условия минимальности времени прохождения и минимальности оптической длины пути эквивалентны. Пусть свет распространяется в однородной среде с абсолютным показателем преломления n от точки 1 к точке 2, расстояние между которыми равно s
(рис. 68 а).
Оптической длиной пути называется величина:
L = ns.
Если показатель преломления n
меняется при переходе от одной точ- Рис. 68 ки среды к другой (среда неоднородная), то свет будет распростра-
няться, вообще говоря, по некоторой кривой линии (рис. 68 б). В этом случае оптическая длина пути света определяется через интеграл вдоль
кривой:
2
L = n(s)ds.
1
Время распространения света из точки 1 в точку 2 равно
22
t = |
ds |
= |
nds |
= |
L |
, |
(22.1) |
|
V |
c |
|
c |
|||||
|
|
|
|
|
|
|||
11
где V = c/n — фазовая скорость света в среде с абсолютным показателем преломления n, c — скорость света в вакууме, L — оптическая длина пути.
Из соотношения (22.1) видно, что минимальному времени распространения света из точки 1 в точку 2 соответствует минимальная оптическая длина пути L и наоборот.
На основе принципа Ферма можно доказать законы отражения и преломления света.

106 Введение в оптику [ Гл. IV
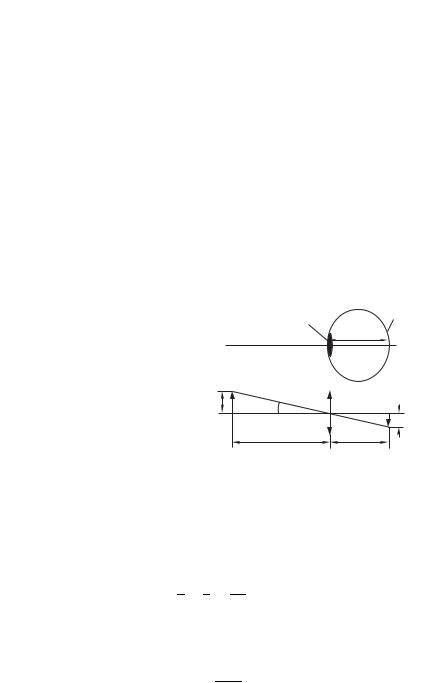
Пусть свет попадает из точки A в точку B пространства, отразившись от плоской границы M N двух сред в точке O (рис. 69). В соответствии с принципом Ферма точка O
|
C |
B |
должна быть расположена на границе |
|
A |
|
сред так, что длина пути AOB минималь- |
||
|
|
|||
|
|
|
|
на. Рассмотрим точку A1, симметричную |
M |
|
|
N точке A относительно линии M N . Длины |
|
|
O |
|||
|
|
|
отрезков AO и A1O одинаковы, длина пу- |
|
|
|
|
|
|
A1 |
|
|
ти AOB равна длине A1OB. Если точки |
|
|
|
A1 и B фиксированы, а положение точ- |
||
|
D |
|
||
|
|
ки O на прямой M N меняется, то длина |
||
|
|
|
|
|
|
Рис. 69 |
|
пути A1OB будет минимальной при усло- |
|
|
|
|
|
вии, что точки A1, O и B лежат на одной |
прямой. В этом случае углы A1OD и COB равны как вертикальные (CD — перпендикуляр к границе M N ). Угол A1OD равен углу AOC по построению точки A1. Следовательно,
AO = COB, то есть угол падения |
|
A |
C |
|
|
||
|
|
|
|
|
|||
луча равен углу его отражения. Закон |
|
|
|
s1 |
|
|
|
отражения света доказан. |
n1 |
|
x |
|
O (MN x) N |
||
Пусть теперь свет распространяется |
|
|
|
|
|
|
|
n2 |
M |
|
|
|
|
||
из точки A среды с абсолютным показа- |
|
|
s2 |
|
|||
|
|
|
|
|
|
||
телем преломления n1 в точку B среды |
|
|
|
|
|
|
|
|
|
|
D |
B |
|||
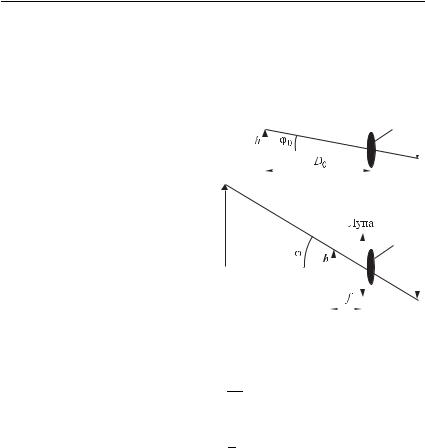
с абсолютным показателем преломления n2 (рис. 70). В соответствии с принципом Ферма точка O, в которой преломляется
луч, должна быть расположена так, чтобы была минимальной оптиче-
ская длина пути LAOB = n1s1 + n2s2, где s1 — длина отрезка AO, s2 — длина отрезка OB. Найдем минимум функции LAOB :
LAOB = n1s1 + n2s2 = n1 AM 2 + x2 + n2 BN 2 + (M N − x)2 ,
где AM и BN — длины перпендикуляров, опущенных из точек A и B на прямую M N — границу раздела сред; x — длина отрезка M O, (M N − x) — длина отрезка ON. Продифференцируем LAOB по переменной x и приравняем производную к нулю:
|
|
|
|
|
|
dLAOB |
= 0, |
|
|
||||
|
|
|
|
|
|
|
|
dx |
|
||||
n |
|
|
x |
− |
n |
|
|
M N − x |
|
= 0, |
|||
|
|
|
|
|
|
||||||||
1 AM 2 + x2 |
2 BN 2 + (M N − x)2 |
||||||||||||
|
|
|
|||||||||||
n1 cos M OA − n2 cos N OB = 0,
Прямая CD перпендикулярна к границе раздела двух сред и проходит через точку O, поэтому cos M OA = sin AOC, cos N OB =
§ 23 ] |
Увеличение оптических приборов, вооружающих глаз |
107 |
|||||||
= sin DOB. Отсюда: |
|
|
|
|
|
|
|||
|
|
|
n1 sin AOC − n2 sin DOB = 0. |
|
|
||||
|
Это соотношение представляет собой математическое выражение |
||||||||
закона преломления. |
|
|
|
|
|
|
|||
|
|
§ 23. Увеличение оптических приборов, |
|
||||||
|
|
|
|
вооружающих глаз |
|
|
|||
|
Подробный анализ оптических систем методами геометрической |
||||||||
оптики выходит за рамки данного учебного пособия. В этом пара- |
|||||||||
графе приводятся краткие сведения о принципах работы некоторых |
|||||||||
оптических приборов в связи с последующим обсуждением понятия |
|||||||||
разрешающей способности (см. § 39). |
|
|
|
||||||
|
Глаз как оптическая система. |
Глаз можно рассматривать как |
|||||||
оптическую систему, состоящую из собирающей линзы (хрусталика) |
|||||||||
и экрана наблюдения (сетчатой оболочки или коротко сетчатки), на |
|||||||||
котором формируется изображе- |
|
|
|
Сетчатка |
|||||
ние |
предметов (рис. |
71). Зра- |
|
Хрусталик |
|
||||
чок |
глаза, |
ограничивая |
диа- |
|
|
|
|||
|
|
~b |
|
||||||
метр проходящего через хруста- |
|
|
|
||||||
|
|
|
|
||||||
лик светового пучка, выполняет |
|
|
|
|
|||||
роль диафрагмы. На каком бы |
|
|
|
|
|||||
расстоянии a от глаза ни на- |
|
|
|
|
|||||
ходился рассматриваемый пред- |
h |
|
|
|
|||||
мет, расстояние b между хру- |
|
|
|
h |
|||||
сталиком и сетчаткой остает- |
|
a |
b |
|
|||||
ся неизменным. Для того что- |
|
|
|
|
|||||
бы |
при изменении расстояния |
|
Рис. 71 |
|
|
||||
a |
между |
предметом |
и |
лин- |
|
|
|
||
|
|
|
|
||||||
зой (хрусталиком) изображение |
|
|
|
|
|||||
предмета располагалось на одном и том же фиксированном расстоянии |
|||||||||
b от линзы (на сетчатке), фокусное расстояние, которое мы обозначим |
|||||||||
как fхр (в данном случае речь идет о фокусном расстоянии хрусталика |
|||||||||
глаза), должно меняться. При выполнении указанного условия, как |
|||||||||
следует из формулы тонкой линзы: |
|
|
|
|
|||||
1 + 1 = 1 , a b fхр
фокусное расстояние хрусталика глаза является функцией расстояния a между предметом и глазом, тогда как значение расстояния b между хрусталиком и сетчаткой фиксировано:
ab fхр = a + b .
108 |
Введение в оптику |
[ Гл. IV |
Аккомодацией глаза называется процесс изменения фокусного расстояния хрусталика с целью получения четкого изображения рассматриваемого предмета на сетчатке. При аккомодации изменяется кривизна внешних поверхностей хрусталика благодаря усилиям глазных мышц.
Углом зрения называется угол, под которым виден предмет из оптического центра хрусталика (см. рис. 71, где угол зрения обозначен через ϕ).
Поскольку изображение предмета всегда формируется в плоскости, расположенной на фиксированном расстоянии B от линзы, для построения создаваемого линзой изображения любой точки предмета достаточно провести из этой точки один луч, проходящий через оптический центр линзы, до пересечения с указанной фиксированной плоскостью. Если предмет в виде отрезка прямой линии расположен перпендикулярно к главной оптической оси системы, а угол зрения равен ϕ, то размер h изображения предмета на сетчатке равен:
h = b tg ϕ, |
(23.1) |
где B — расстояние от линзы (хрусталика) до экрана наблюдения (сетчатки).
Чем ближе предмет располагается к глазу, тем больше размер его изображения, и тем лучше видны мелкие детали предмета. Однако при этом в процессе аккомодации глаза сильнее должны искривляться преломляющие поверхности хрусталика, что приводит к утомлению.
Расстоянием наилучшего зрения называется расстояние между предметом и глазом, при котором достаточно хорошо различаются детали предмета, но не возникает чрезмерного напряжения и утомления глаза. Расстояние наилучшего зрения приблизительно составляет D0 ≈ ≈ 25 см.
Оптические приборы, вооружающие глаз, делятся на две группы: приборы для наблюдения мелких предметов (лупа, микроскоп) и приборы для наблюдения удаленных объектов (зрительная труба, бинокль и т. д.). Независимо от предназначения принцип действия всякого вооружающего глаз оптического прибора состоит в том, чтобы с его помощью увеличить угол зрения при рассматривании того или иного объекта, в результате чего увеличивается размер изображения предмета на сетчатке глаза, лучше различаются мелкие детали объекта наблюдения.
Увеличением оптического прибора Γ называется отношение линейных размеров изображения на сетчатке глаза при наблюдении предмета вооруженным и невооруженным глазом:
Γ = |
hвооруж |
. |
(23.2) |
|
hневооруж |
||||
|
|
|
С учетом соотношения (23.1) увеличение Γ оптического прибора равно отношению тангенсов углов зрения ϕ и ϕ0 при рассматривании
§ 23 ] |
Увеличение оптических приборов, вооружающих глаз |
109 |
предмета вооруженным и невооруженным глазом соответственно:
Γ = |
hвооруж |
= |
tg ϕ |
(23.3) |
|
|
|
. |
|||
|
tg ϕ |
||||
|
hневооруж |
0 |
|
|
|
Увеличение лупы. Лупа представляет собой |
короткофокусную |
||||
собирающую линзу, которую помещают между предметом и глазом так,
что предмет располагается вбли- |
|
|
|
|
|
|
|
|
|
|
|
|||||
зи |
переднего |
фокуса |
линзы. |
Хрусталик |
||||||||||||
Мнимое изображение |
предме- |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
та |
удалено «на |
бесконечность». |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
При |
рассматривании |
изображе- |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
ния глаз аккомодирован «на бес- |
|
|
|
|
|
|
|
|
|
|
|
|||||
конечность», так что напряжение |
|
|
|
|
|
|
|
|
|
|
|
|||||
глазных мышц минимально. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
В |
соответствии |
формулой |
|
|
|
|
|
|
|
Хрусталик |
|||||
(23.3) увеличение Γ |
лупы равно |
|
|
|
|
|
|
|
||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
отношению тангенса угла зрения |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
ϕ, под которым предмет виден |
|
|
|
|
|
|
|
|
|
|
|
|||||
через лупу, к тангенсу угла |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
зрения ϕ0, под которым виден |
|
|
|
|
|
|
|
|
|
|
|
|||||
расположенный |
на |
расстоянии |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
наилучшего зрения предмет при |
Рис. 72 |
|
его рассматривании невооружен- |
||
|
ным глазом. Из чертежа на рис. 72 вытекают соотношения:
h tg ϕ0 = D0 ,
где h — размер предмета, D0 — расстояние наилучшего зрения; tg ϕ = fh ,
где f — фокусное расстояние лупы. Увеличение лупы равно
Γ = |
tg ϕ |
= |
D0 |
. |
|
|
|||
|
tg ϕ0 |
f |
||
Обычно f = 1 ÷ 10 см. При значении D0 = 25 см увеличение лупы находится в пределах 2, 5 ÷ 25.
Увеличение микроскопа. Световой микроскоп служит для рассматривания мелких предметов путем получения больших угловых увеличений. Он состоит из двух короткофокусных систем — объектива и окуляра.
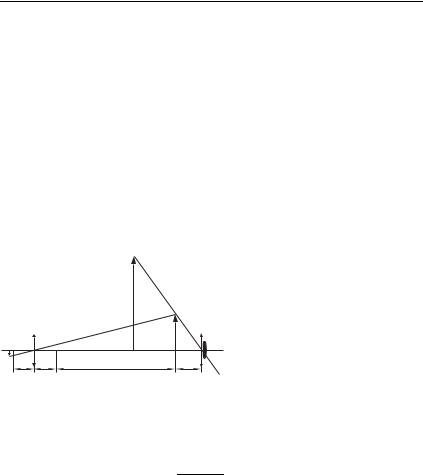
Фокусные расстояния собирающих линз, выполняющих функции объектива и окуляра, обозначим через fоб и fок соответственно. Предмет размером h располагается вблизи переднего фокуса объектива, а создаваемое объективом изображение размером H находится вблизи переднего фокуса окуляра (рис. 73). Линейное увеличение объектива
110 Введение в оптику [ Гл. IV
(то есть отношение размера изображения H к размеру предмета h) приблизительно равно
H |
≈ |
fоб + |
≈ |
|
, |
h |
fоб |
fоб |
где — расстояние между фокусами объектива и окуляра, которое много больше самих фокусных расстояний fоб и fок.
Отсюда следует
H ≈ h |
|
. |
(23.4) |
fоб |
Тангенс угла ϕ, под которым видно изображение предмета через окуляр, с учетом (23.4) равен
tg ϕ = |
H |
≈ |
h |
(23.5) |
|
|
|
. |
|||
fок |
fобfок |
||||
Тангенс угла зрения ϕ0, под которым виден предмет невооруженным глазом, равен
|
|
|
|
H |
h |
fîá |
fîá |
|
fîê |
|
Рис. 73
tg ϕ0 = |
h |
, |
(23.6) |
|
|||
|
D0 |
|
|
где D0 — расстояние наилучшего зрения.
Увеличение микроскопа Γ найдем, поделив равенства (23.5) и (23.6) друг на друга:
Γ = |
tg ϕ |
= |
D0 |
. (23.7) |
|
|
|||
|
tg ϕ0 |
fобfок |
||
Для типовых значений параметров микроскопа fоб = 2, 5 мм, fок = = 15 мм, = 160 мм, D0 = 250 мм вычисленное по формуле (23.7) увеличение Γ приблизительно равно:
Γ = 160 · 250 ≈ 1000. 2, 5 · 15
Величина 1000 является предельно возможной для световых микроскопов. Как правило, увеличение хороших световых микроскопов составляет несколько сотен.
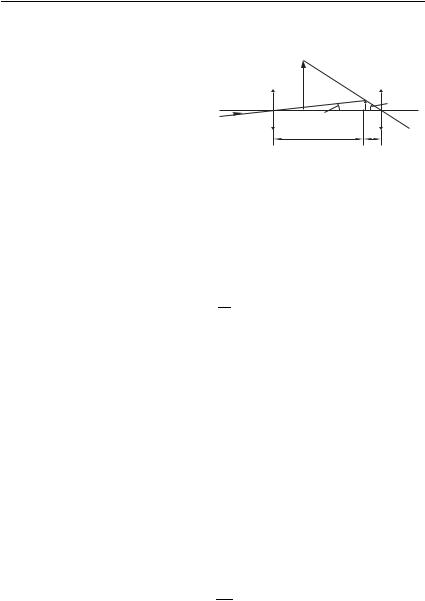
Увеличение зрительной трубы. Зрительная труба предназначена для рассматривания удаленных предметов. Рассмотрим один из типов зрительной трубы (труба Кеплера), которая состоит из двух собирающих линз — объектива и окуляра с фокусными расстояниями fоб и fок соответственно, при этом выполняется условие fоб fок.
Из оптического центра объектива зрительной трубы и из оптического центра хрусталика невооруженного глаза удаленный предмет виден под одним и тем же углом зрения ϕ0. При рассматривании предмета в зрительную трубу изображение, формируемое объективом, располагается в задней фокальной плоскости объектива, которая приблизительно
§ 23 ] |
Увеличение оптических приборов, вооружающих глаз |
111 |
совпадает с передней фокальной плоскостью окуляра (рис. 74). Поперечный размер H изображения, формируемого объективом, можно выразить через параметры fоб
и ϕ0:
H = fоб tg ϕ0.
Тангенс угла ϕ, под которым видно изображение предмета через окуляр, равен:
|
|
H |
|
|
|
|
îê |
От предмета |
0 îá |
|
|
fîá |
fîê |
|
|
|
|
|
H |
= |
fоб tg ϕ0 |
. |
|
tg ϕ = fок |
fок |
Рис. 74 |
|||
|
|
|
|
|
|
Отсюда получим увеличение зрительной трубы, равное, согласно
(23.3), отношению тангенсов углов ϕ и ϕ0: |
|
||||
Γ = |
tg ϕ |
= |
fоб |
. |
(23.8) |
tg ϕ0 |
|
||||
|
|
fок |
|
||
Если углы ϕ0 и ϕ не слишком велики, отношение тангенсов можно приближенно заменить отношением самих углов, выраженных в ради-
анах: |
ϕ |
(23.9) |
|
≈ |
|||
ϕ0 . |
Вэтом случае величина Γ показывает, во сколько раз угол зрения
ϕпри рассматривании предмета через зрительную трубу больше угла
зрения ϕ0 при рассматривании предмета невооруженным глазом.
Как отмечалось выше, из оптического центра объектива зрительной трубы и из оптического центра хрусталика невооруженного глаза уда-
ленный предмет виден под одним и тем же углом ϕ0, который в связи с указанным обстоятельством можно обозначить как ϕоб:
ϕ0 = ϕоб. |
(23.10) |
Таким образом, ϕоб — угол, под которым из оптического центра объектива виден удаленный предмет и видно локализованное в фокальной плоскости объектива изображение этого предмета.
Угол ϕ, под которым через окуляр зрительной трубы видно сформированное объективом изображение предмета, обозначим как ϕок:
ϕок = ϕ. |
||
В новых обозначениях (23.10) и (23.11) |
||
трубы (23.9) |
ϕок |
|
≈ |
||
ϕоб . |
||
(23.11)
увеличение зрительной
(23.12)
Здесь величина Γ показывает, во сколько раз угловой размер изображения предмета, расположенного в фокальной плоскости объектива, при рассматривании через окуляр больше, чем при его рассматривании из оптического центра объектива. Данная интерпретация увеличения будет использоваться в дальнейшем (см. § 39).
