
- •Оглавление
- •Предисловие
- •§ 1. Гармонические колебания
- •§ 2. Затухающие колебания
- •§ 3. Вынужденные колебания. Резонанс
- •§ 4. Векторная диаграмма напряжений
- •§ 5. Связь добротности с формой резонансных кривых
- •§ 6. Переменный ток
- •§ 7. Вынужденные колебания в параллельном контуре
- •§ 8. Метод комплексных амплитуд
- •Задачи
- •§ 9. Волновое уравнение и его решения
- •§ 10. Скорость и энергия упругих волн в твердой среде
- •§ 11. Перенос энергии упругой волной
- •§ 12. Стоячая волна
- •§ 13. Характеристики звука. Эффект Доплера для звуковых волн
- •Задачи
- •§ 14. Векторное волновое уравнение для электромагнитного поля
- •§ 15. Плоская электромагнитная волна и ее свойства
- •§ 16. Энергия электромагнитных волн
- •§ 17. Импульс и давление электромагнитного поля
- •§ 18. Дипольное излучение
- •Задачи
- •§ 19. Свойства световой волны. Законы отражения и преломления
- •§ 20. Формулы Френеля. Закон Брюстера
- •§ 21. Фотометрические величины и единицы
- •§ 22. Законы геометрической оптики. Принцип Ферма
- •§ 23. Увеличение оптических приборов, вооружающих глаз
- •Задачи
- •§ 24. Интерференция световых волн от двух когерентных источников
- •§ 25. Интерференция двух плоских волн
- •§ 27. Фурье-спектр световой волны
- •§ 28. Пространственная когерентность
- •§ 29. Интерференция в тонких пластинках
- •§ 30. Интерференционный опыт с бипризмой Френеля
- •Задачи
- •§ 33. Дифракция Френеля от щели
- •§ 34. Дифракция Фраунгофера от щели
- •§ 35. Количественный критерий вида дифракции
- •§ 36. Многолучевая интерференция
- •§ 37. Дифракционная решетка
- •§ 38. Дифракционная решетка как спектральный прибор
- •§ 39. Разрешающая сила объектива и оптимальное увеличение зрительной трубы
- •Задачи
- •§ 40. Поляризованный и естественный свет. Закон Малюса
- •§ 41. Поляризация света при отражении и преломлении
- •§ 42. Двойное лучепреломление
- •§ 43. Вращение плоскости поляризации
- •Задачи
- •§ 44. Дисперсия света. Групповая скорость
- •§ 45. Элементарная теория дисперсии
- •§ 46. Поглощение и рассеяние света
- •Задачи
- •Ответы к задачам
- •Приложения
- •Электрические колебания
- •Гармонические колебания
- •Затухающие колебания
- •Вынужденные колебания
- •Упругие волны
- •Электромагнитные волны
- •Свойства световой волны
- •Фотометрия
- •Интерференция света
- •Когерентность
- •Дифракция света
- •Поляризация света
- •Дисперсия света
- •II. Производные единицы СИ электрических, магнитных и световых величин
- •III. Постоянные некоторых веществ
- •Предметный указатель

Г Л А В А I
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
§ 1. Гармонические колебания
Классификация колебаний. Электрические колебания представляют собой движение электрических зарядов, которое повторяется через определенные или почти определенные промежутки времени. Так, если к обкладкам заряженного конденсатора подключить катушку индуктивности, начнется периодически повторяющееся перетекание зарядов с одной обкладки на другую и обратно.
Колебательным контуром называется электрическая цепь, обладающая емкостью и индуктивностью, то есть цепь, имеющая в своем составе помимо прочих элементов конденсатор и катушку индуктивности (или несколько конденсаторов и катушек). Наличие емкости и индуктивности является необходимым условием возникновения собственных электрических колебаний в цепи. Следует заметить, что любой проводник и любая электрическая цепь, не предназначенные специально для создания и поддержания электрических колебаний, обладают некоторой емкостью и некоторой индуктивностью.
Периодом колебаний T называется промежуток времени, через который движение электрических зарядов повторяется.
В процессе электрических колебаний изменяются величина заряда на обкладках конденсатора, сила тока в цепи, напряжения на различных элементах колебательного контура. Амплитудой колебаний называется величина наибольшего отклонения соответствующего физического параметра (заряда, тока, напряжения) от своего равновесного значения.
Свободными называются колебания физической системы (электрической или механической) около положения устойчивого равновесия после того, как система была выведена из состояния равновесия и предоставлена самой себе. Состояние устойчивого равновесия соответствует минимуму потенциальной энергии системы.
Для электрической цепи в качестве потенциальной энергии можно рассматривать энергию заряженного конденсатора. Энергия конденсатора минимальна, если заряд на его обкладках равен нулю. Зарядив конденсатор, мы выводим систему из состояния равновесия. Если обкладки конденсатора соединить с концами катушки индуктивности, то возникнут свободные электрические колебания — заряд будет перетекать с одной обкладки на другую и этот процесс будет повторяться.
Если омическое сопротивление колебательного контура пренебрежимо мало, то свободные колебания являются гармоническими. Это
10 Электрические колебания [ Гл. I
означает, что изменение во времени величин заряда, тока, напряжений на различных элементах контура происходит по гармоническому закону (описывается функцией синуса или косинуса).
Частота гармонических колебаний ω0 в контуре, омическое сопротивление которого равно нулю, называется собственной частотой контура.
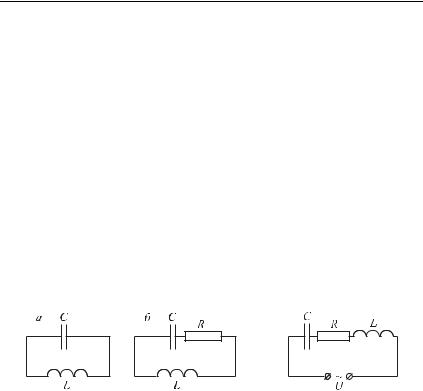
Колебания в контуре при наличии в нем омического сопротивления называются затухающими. В процессе колебаний в таком контуре электрическая энергия — энергия электрического поля конденсатора и энергия магнитного поля катушки индуктивности — будет постепенно превращаться в тепло, выделяемое на омическом сопротивлении. Примеры электрических цепей, в которых возможны свободные гармонические и свободные затухающие колебания, представлены на рисунках 1 а и 1 б соответственно.
Вынужденными колебаниями называются колебания, возникающие в электрической цепи в результате внешнего воздействия и происходящие в такт с изменениями этого воздействия.
Примером внешнего воздействия служит поданное на вход контура переменное напряжение U = Um cos ωt (рис. 2).
Рис. 1 |
Рис. 2 |
Условие квазистационарности тока. Для описания колебаний в электрических цепях можно воспользоваться законом Ома, который, строго говоря, хотя и справедлив только для цепей постоянного тока, однако, если токи и напряжения в цепи изменяются не слишком быстро, то для мгновенных значений тока и напряжения закон Ома остается в силе.
Напомним, что ток называется квазистационарным при условии, что во всех поперечных сечениях проводников, соединенных между собой последовательно и составляющих электрическую цепь, мгновенное значение силы тока приблизительно одинаково в один и тот же момент времени. Воспользуемся законом Ома для описания этих токов.
Пусть по некоторой цепи течет изменяющийся во времени ток. Условие квазистационарности будет выполнено, если за время распространения по цепи электромагнитного возмущения сила тока успевает измениться незначительно. Электромагнитным возмущением является, например, скачкообразное изменение напряженности электрического поля во всех участках цепи. Скорость распространения возмущения по

§ 1 ] |
Гармонические колебания |
11 |
порядку величины равна скорости распространения электромагнитных волн в вакууме c.
Оценим частоту ν переменного тока, для которого выполнено условие квазистационарности. Промежуток времени, в течение которого сила переменного тока успевает существенно измениться, приблизительно равен периоду колебаний T тока. Если l — длина цепи, c — скорость распространения электромагнитного возмущения (скорость света в вакууме), то время τ передачи возмущения по цепи равно
τ = cl .
Условие квазистационарности тока:
τ = cl T.
Частота ν переменного тока при этом должна удовлетворять усло- вию: ν = T1 cl .
Для цепи длиной l ≈ 3 м и скорости света в вакууме ≈ 3 · 108 /c условие квазистационарности выполняется, если частота ν переменного тока удовлетворяет условию:
ν 108 |
. |
Уравнение гармонических колебаний и его решения. Рассмотрим колебательный контур, в состав которого входит конденсатор емкости C, катушка индуктивности L, при этом сопротивление катушки и соединительных проводов пренебрежимо мало (R = 0). Пусть в некоторый момент времени по контуру течет ток силой I, на обкладках
конденсатора сосредоточен заряд q, потенциалы |
|
|
|
|
|
|
|
||||
обкладок равны ϕ1 и ϕ2 (рис. 3). |
|
q |
C |
q |
|||||||
|
|||||||||||
Запишем закон Ома для участка контура, |
|
|
|
|
|
|
|
||||
1 |
|
2 |
|
|
|
||||||
расположенного между точками с потенциалами |
|
|
|
|
|||||||
|
|||||||||||
ϕ1 и ϕ2 и содержащего катушку индуктивности: |
|
|
|
|
|
|
I |
||||
IR = ϕ1 − ϕ2 − L |
dI |
, |
|
|
|
|
|
|
|
||
|
|
L |
|||||||||
dt |
|
|
|||||||||
где величина −L |
dI |
представляет собой ЭДС |
|
Рис. 3 |
|||||||
dt |
|
||||||||||
самоиндукции. |
|
|
|
|
|
|
|
||||
Учтем, что ϕ1 − ϕ2 = −Cq , R = 0, сила тока I связана с величиной заряда конденсатора q следующим соотношением:
I = dqdt .
Тогда получим
q¨ + LC1 q = 0,

12 Электрические колебания [ Гл. I
или |
q¨ + ω02q = 0, |
(1.1) |
||||||
|
||||||||
где введены обозначения q¨ = |
d2q |
, ω0 |
= |
√ |
1 |
|
— собственная частота |
|
2 |
||||||||
контура. |
|
dt |
|
|
LC |
|
||
|
|
|
|
|
|
|
|
|
Уравнение (1.1) представляет собой уравнение гармонических ко-
лебаний, общее решение которого имеет вид |
|
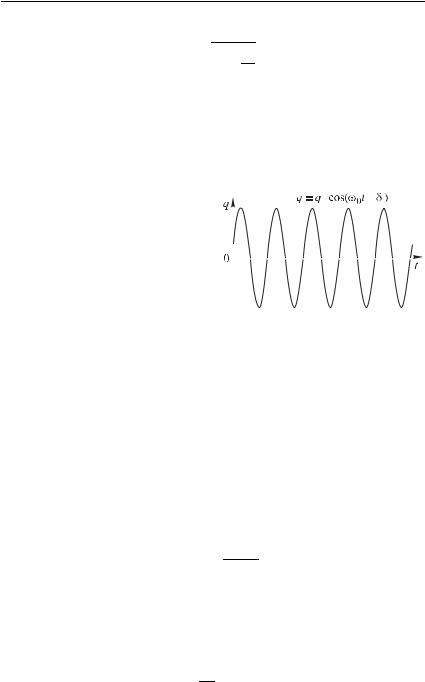
q = qm cos (ω0t + δ). |
(1.2) |
Из (1.2) видно, что заряд на обкладках конденсатора меняется с течением времени по гармоническому закону. Величина qm — это амплитуда колебаний заряда, (ω0t + δ) — фаза колебаний, δ — начальная фаза, ω0 — циклическая частота колебаний (она равна собственной частоте контура). Напомним, что единицей циклической частоты в
системе СИ является обратная секунда |
|
[ω0] = −1 . |
Период колебаний заряда связан с |
циклической частотой следую- |
|
|
|
|
щим соотношением:
T= 2π .
ω0
Период измеряется в секундах ([T ] = ).
Частота колебаний ν равна величине, обратной периоду:
ν = T1 ,
и измеряется в обратных секундах или герцах ([ν] = −1 = ). Сила тока в контуре в произвольный момент времени равна
I = |
dq |
= −qmω0 sin (ω0t + δ) = qmω0 cos ω0t + δ + |
π |
|
= |
|
|
dt |
2 |
π |
|
||||
|
|
= Im cos ω0t + δ + |
|
, (1.3) |
|||
|
|
2 |
|||||
где Im = qmω0 — амплитуда колебаний тока.
Частота свободных гармонических колебаний определяется параметрами контура — его индуктивностью L и емкостью C. Амплитуда колебаний qm и начальная фаза δ от параметров контура не зависят, а определяются так называемыми начальными условиями, а именно, величиной q0 заряда конденсатора и силой тока I0 в начальный момент времени.
Выразим величины q0 и I0 в момент времени t = 0 с помощью формул (1.2) и (1.3):
q0 = qm cos δ,
I0 = −qmω0 sin δ.
§ 1 ] |
Гармонические колебания |
13 |
Из этих двух соотношений найдем
2
qm = q02 + I02 ,
ω0
tg δ = − I0 . q0ω0
График зависимости от времени t заряда конденсатора q при гармонических колебаниях представлен на рис. 4.
Установим связь между фазами колебаний тока в цепи и напряжения на конденсаторе при гармонических колебаниях. Напряжение на конденсаторе равно
UC = |
q |
= |
qm |
cos (ω0t + δ). (1.4) |
|
m |
|
||||||
|
|
|||||
|
|
|
|
|||
C |
|
C |
|
|
||
Сравнивая (1.4) и (1.3), видим, |
|
|
||||
что при гармонических колебани- |
|
|
||||
|
|
|||||
ях ток опережает по фазе напря- |
|
|
||||
жение на конденсаторе на π/2. |
|
|
||||
Разность потенциалов на кон- |
|
|
||||
цах катушки индуктивности рав- |
|
Рис. 4 |
||||
на по величине и противоположна |
|
|||||
по знаку (при выбранном направлении обхода контура) разности потенциалов на обкладках конденса-
тора, то есть напряжение на катушке равно:
UL = −UC = − |
qm |
cos (ω0t + δ) = |
qm |
cos (ω0t + δ + π). |
(1.5) |
C |
C |
Сравнивая (1.5) с (1.3), видим, что колебания напряжения на катушке опережают по фазе колебания тока в цепи на величину π/2.
Энергия гармонических колебаний. Энергия W гармонических
колебаний равна сумме энергии конденсатора |
q2 |
|
и энергии тока (маг- |
|||||||||||||||||
|
||||||||||||||||||||
нитного поля) в катушке LI2/2: |
|
|
|
|
|
2C |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
q2 |
LI2 |
|
qm2 |
2 |
|
|
Lqm2 ω02 |
2 |
|
|
|
|
|
||||||
W = |
|
+ |
|
|
|
= |
|
cos (ω0t + δ) + |
2 |
sin |
(ω0t + δ) = |
|||||||||
2C |
2 |
|
2C |
|||||||||||||||||
|
|
|
|
qm2 |
2 |
|
Lqm2 |
2 |
|
|
|
|
|
|
|
qm2 |
||||
|
|
= |
|
cos (ω0t + δ) + |
|
sin |
(ω0t + δ) = |
|
= const, (1.6) |
|||||||||||
|
|
2C |
2LC |
2C |
||||||||||||||||
где в преобразованиях было учтено, что ω2 |
= |
1 |
. |
|
|
|||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
LC |
|
|
|||||
Из полученного выражения (1.6) видно, что полная энергия гармо-
нических колебаний W не зависит от времени и равна максимальному
2
значению энергии конденсатора 2qmC . Величина W равна также макси-
