
- •Оглавление
- •Предисловие
- •§ 1. Гармонические колебания
- •§ 2. Затухающие колебания
- •§ 3. Вынужденные колебания. Резонанс
- •§ 4. Векторная диаграмма напряжений
- •§ 5. Связь добротности с формой резонансных кривых
- •§ 6. Переменный ток
- •§ 7. Вынужденные колебания в параллельном контуре
- •§ 8. Метод комплексных амплитуд
- •Задачи
- •§ 9. Волновое уравнение и его решения
- •§ 10. Скорость и энергия упругих волн в твердой среде
- •§ 11. Перенос энергии упругой волной
- •§ 12. Стоячая волна
- •§ 13. Характеристики звука. Эффект Доплера для звуковых волн
- •Задачи
- •§ 14. Векторное волновое уравнение для электромагнитного поля
- •§ 15. Плоская электромагнитная волна и ее свойства
- •§ 16. Энергия электромагнитных волн
- •§ 17. Импульс и давление электромагнитного поля
- •§ 18. Дипольное излучение
- •Задачи
- •§ 19. Свойства световой волны. Законы отражения и преломления
- •§ 20. Формулы Френеля. Закон Брюстера
- •§ 21. Фотометрические величины и единицы
- •§ 22. Законы геометрической оптики. Принцип Ферма
- •§ 23. Увеличение оптических приборов, вооружающих глаз
- •Задачи
- •§ 24. Интерференция световых волн от двух когерентных источников
- •§ 25. Интерференция двух плоских волн
- •§ 27. Фурье-спектр световой волны
- •§ 28. Пространственная когерентность
- •§ 29. Интерференция в тонких пластинках
- •§ 30. Интерференционный опыт с бипризмой Френеля
- •Задачи
- •§ 33. Дифракция Френеля от щели
- •§ 34. Дифракция Фраунгофера от щели
- •§ 35. Количественный критерий вида дифракции
- •§ 36. Многолучевая интерференция
- •§ 37. Дифракционная решетка
- •§ 38. Дифракционная решетка как спектральный прибор
- •§ 39. Разрешающая сила объектива и оптимальное увеличение зрительной трубы
- •Задачи
- •§ 40. Поляризованный и естественный свет. Закон Малюса
- •§ 41. Поляризация света при отражении и преломлении
- •§ 42. Двойное лучепреломление
- •§ 43. Вращение плоскости поляризации
- •Задачи
- •§ 44. Дисперсия света. Групповая скорость
- •§ 45. Элементарная теория дисперсии
- •§ 46. Поглощение и рассеяние света
- •Задачи
- •Ответы к задачам
- •Приложения
- •Электрические колебания
- •Гармонические колебания
- •Затухающие колебания
- •Вынужденные колебания
- •Упругие волны
- •Электромагнитные волны
- •Свойства световой волны
- •Фотометрия
- •Интерференция света
- •Когерентность
- •Дифракция света
- •Поляризация света
- •Дисперсия света
- •II. Производные единицы СИ электрических, магнитных и световых величин
- •III. Постоянные некоторых веществ
- •Предметный указатель

§ 20 ] Формулы Френеля. Закон Брюстера 93
Законы отражения (19.9) и преломления (19.10) доказаны.
Явление полного внутреннего отражения. Рассмотрим световую волну, которая переходит из среды с показателем преломления n1 в среду с показателем преломления n2, причем n1 > n2 (рис. 57). При указанном соотношении абсолютных показателей преломления принято говорить, что первая среда является оптически более плотной, чем вторая.
Предельным углом полного внутреннего отражения θпред называется такой угол падения, для которого угол преломления равен 90 ◦.
В этом случае закон преломления |
|
|
|
|
|
|
|
|
имеет вид |
|
1 |
|
|
|
ïðåä |
|
|
|
|
|
|
|
||||
n1 sin θпред = n2 sin 90 ◦ = n2. |
n1 |
|
|
n1 |
|
|||
|
|
|
|
|
|
|||
Отсюда находим: |
n2 |
|
2 |
|
n2 |
|
90 |
|
|
|
|
|
|
|
|||
sin θпред = n2/n1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При углах падения, превышающих предельный угол, световая вол-
на проникает во вторую среду лишь на расстояния порядка длины волны λ и возвращается в первую среду. В этом случае преломленный луч во второй среде не распространяется. Это явление называется полным внутренним отражением. Явление полного внутреннего отражения можно наблюдать только при переходе света из оптически более плотной в оптически менее плотную среду.
§ 20. Формулы Френеля. Закон Брюстера
Формулы Френеля. Снова обозначим через n1 и n2 абсолютные показатели преломления двух однородных изотропных прозрачных диэлектрических сред, имеющих плоскую поверхность раздела. Плоская световая волна переходит из первой среды во вторую, при этом углы падения и отражения равны θ1, а угол преломления θ2. Установим соотношения между амплитудами колебаний светового вектора в падающей, отраженной и преломленной волнах.
Ниже будет показано, что как естественный, так и поляризованный свет может быть представлен как наложение (суперпозиция) световых волн, поляризованный в двух взаимно перпендикулярных плоскостях. Учитывая это обстоятельство, достаточно рассмотреть закономерности отражения и преломления света на поверхности раздела диэлектриков только для двух типов волн: 1) волна, в которой колебания светового вектора происходят в плоскости падения; 2) волна, в которой направление колебаний светового вектора перпендикулярно плоскости падения.
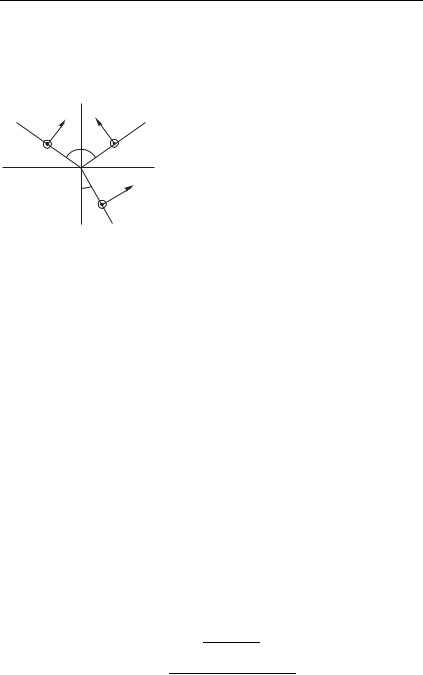
С л у ч а й 1 (плоскость колебаний светового вектора совпадает с плоскостью падения). На рис. 58 изображены в некоторый момент
94 |
|
|
|
Введение в оптику |
[ Гл. IV |
времени векторы напряженности электрического поля E, E и E и |
|||||
магнитного поля H, H и H в падающей, отраженной и преломленной |
|||||
волнах соответственно. Будем считать, что вектор E задан, и выразим |
|||||
через него векторы E и E . С этой целью запишем граничные условия |
|||||
для тангенциальных компонент векторов напряженности электричес- |
|||||
|
|
|
|
кого и магнитного поля на поверхно- |
|
|
E |
E |
|
сти раздела сред (см. в кн. 3 «Электро- |
|
|
|
магнетизм», § 10 и |
30). Тангенциальные |
||
|
|
|
|
||
|
1 |
1 |
H |
компоненты суммарного электрического и |
|
n1 |
H |
|
суммарного магнитного поля по разные |
||
n2 |
|
|
|
стороны границы |
раздела диэлектриков |
|
|
|
должны быть одинаковыми: |
||
|
|
2 |
E |
||
|
|
Eτ + Eτ = Eτ , |
|||
|
|
H |
|
||
|
|
|
|
(I) |
|
|
|
|
|
H + H = H . |
|
Рис. 58 |
Поскольку векторы H, H и H в |
|
рассматриваемом случае параллельны по- |
верхности раздела диэлектриков, их тангенциальные компоненты Hτ , Hτ , Hτ равны модулям H, H , H соответствующих векторов, что и отражено во втором уравнении системы (I).
Подставим в первое уравнение системы (I) вытекающие из чертежа на рис. 58 соотношения:
Eτ = E cos θ1, Eτ = −E cos θ1, Eτ = E cos θ2,
где E, E и E — модули векторов E, E и E соответственно. Учитывая связь (19.1) между амплитудами электрической и маг-
нитной составляющей электромагнитной волны, подставим во второе уравнение системы (I) следующие выражения:
H = n1E |
|
μ0 |
, |
H = n1E |
|
|
μ0 |
, |
H = n2E |
|
|
μ0 |
. |
|
|
ε0 |
|
|
|
ε0 |
|
|
|
ε0 |
|||
Воспользовавшись законом преломления света (19.10), заменим показатель преломления n2 через: n2 = n1sin θ1/sin θ2.
В результате выполненных подстановок и преобразований системы (I) получим
E cos θ1 − E cos θ1 = E cos θ2,
E sin θ2 + E sin θ2 = E sin θ1.
Отсюда найдем соотношения между модулями векторов E, E , E :
E = E |
tg(θ1 |
− θ2) |
, |
|
(20.1) |
|
|
||||
|
tg(θ1 |
+ θ2) |
|
|
|
2 sin θ2 cos θ1 |
− θ2) . |
|
|||
E = E sin (θ1 + θ2) cos(θ1 |
(20.2) |
||||

§ 20 ] |
Формулы Френеля. Закон Брюстера |
|
95 |
||||
Соотношения (20.1) и (20.2) устанавливают связь между модуля- |
|||||||
ми E, E , E (а также амплитудами) световых векторов в падаю- |
|||||||
щей, отраженной и преломленной волнах на границе раздела диэлек- |
|||||||
триков. |
|
|
|
|
|
|
|
С л у ч а й 2 |
(плоскость колебаний светового вектора перпендику- |
||||||
лярна к плоскости падения). Пусть векторы напряженности электриче- |
|||||||
ского поля в падающей, отраженной и преломленной волнах E, E и |
|||||||
E перпендикулярны к плоскости паде- |
|
|
|
|
|
||
ния (рис. 59). |
|
|
|
|
|
|
|
Граничные условия для тангенциаль- |
|
E |
|
|
E |
||
ных компонент векторов напряженности |
|
|
1 |
1 |
|
||
|
|
|
|||||
электрического |
и магнитного |
поля на |
n1 |
H |
|
|
H |
поверхности раздела диэлектриков име- |
|
|
|||||
n2 |
|
|
|
|
|||
ют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E + E = E , |
(II) |
|
|
|
2 |
E |
|
Hτ + Hτ = Hτ . |
|
|
|
|
|
|
|
|
|
|
H |
|
|
||
|
|
|
|
|
|
|
|
Поскольку в рассматриваемом случае векторы E, E и E параллельны поверхности раздела диэлектриков, их
тангенциальные компоненты Eτ , Eτ иEτ совпадают с модулями E, E и E соответствующих векторов, что учтено при записи первого уравнения системы (II).
Подставим во второе уравнение системы (II) соотношения:
Hτ = H cos θ1, Hτ = −H cos θ1, Hτ = H cos θ2,
которые вытекают из чертежа рис. 59.
После замены напряженности магнитного поля через напряженность электрического поля:
H = n1E |
|
μ0 |
, |
H = n1E |
|
|
μ0 |
, |
H = n2E |
|
|
μ0 |
; |
|
|
ε0 |
|
|
|
ε0 |
|
|
|
ε0 |
|||
и подстановки показателя преломления n2
sin θ1 n2 = n1 sin θ2 ,
система (II) будет иметь следующий вид:
E + E = E ,
E sin θ2 cos θ1 − E sin θ2 cos θ1 = E sin θ1 cos θ2.
Выразив отсюда E и E через E, найдем соотношения между модулями (а также и амплитудами) световых векторов в падающей,

96 Введение в оптику [ Гл. IV
отраженной и преломленной волнах на поверхности раздела диэлектриков:
E = |
E |
sin (θ1 |
− θ2) |
, |
(20.3) |
|||
sin (θ1 |
||||||||
− |
|
|
+ θ2) |
|
|
|||
E = E |
2 sin θ2 cos θ1 |
. |
(20.4) |
|||||
|
||||||||
|
|
sin (θ1 + θ2) |
|
|
||||
Соотношения (20.1)–(20.4) называются формулами Френеля (1788–1827).
Формулы Френеля не только устанавливают связь между модулями световых векторов в падающей, отраженной и преломленной волнах на границе двух сред, но и содержат информацию о фазовых соотношениях этих волн.
Рассмотрим в качестве примера формулу (20.1). Пусть световая волна, вектор E в которой лежит в плоскости падения, переходит из оптически менее плотной среды с показателем n1 в оптически более плотную среду c показателем n2 (n1 < n2), причем падение света на поверхность раздела почти нормальное. В этих условиях углы θ1 и
θ2 малы, так что выполняются приближенные соотношения: tg θ1,2 |
≈ |
|||||||||
≈ sin θ1,2 ≈ θ1,2. Равенство (20.1) будет иметь вид |
|
|||||||||
E = E tg(θ1 − θ2) |
≈ |
E |
θ1 − θ2 . |
|
||||||
|
tg(θ1 + θ2) |
|
|
θ1 + θ2 |
|
|
||||
В приближении малых углов из |
закона преломления n1 sin θ1 |
= |
||||||||
= n2 sin θ2 получим |
|
|
|
|
|
|
|
|
|
|
|
n1θ1 ≈ n2θ2. |
|
|
|
||||||
Исключая углы θ1 и θ2, найдем |
|
|
|
|
|
|
||||
E |
≈ |
E |
n2 − n1 |
. |
(20.5) |
|||||
|
|
|
n2 + n1 |
|
|
|
||||
Если модуль светового вектора падающей волны E — наперед заданная положительная величина, то, как следует из равенства (20.5) с учетом соотношения n2 − n1 > 0, модуль светового вектора отраженной волны E — также положительная величина. Таким образом, определенные с помощью формул Френеля знаки величин E и E не противоречат исходному предположению о том, как направлены векторы E и E (иначе говоря, направления изображенных на рис. 58 векторов E и E были выбраны правильно).
Как видно из рис. 58, при стремлении угла падения θ1 к нулю векторы E и E направлены навстречу друг другу, что означает скачкообразное изменение фазы электромагнитной волны на величину π при ее отражении.
Итак, из формул Френеля, в частности, следует: при отражении света под малыми углами от оптически более плотной среды фаза волны скачком меняется на величину π. Это утверждение будет использоваться в дальнейшем.

§ 20 ] Формулы Френеля. Закон Брюстера 97
Проанализируем теперь случай почти нормального падения на границу раздела двух диэлектриков световой волны, в которой направление колебаний светового вектора перпендикулярно плоскости падения. С этой целью воспользуемся формулой (20.3). Пусть имеет место
соотношение n1 < n2. Учитывая, что углы θ1 |
и θ2 малы, из (20.3) с |
||||||||||
учетом закона преломления n1 sin θ1 = n2 sin θ2 |
получим |
|
|||||||||
E = |
E |
sin(θ1 |
− θ2) |
E |
θ1 |
− θ2 |
E |
n2 |
− n1 |
. |
(20.6) |
sin(θ1 |
|
|
|||||||||
− |
|
+ θ2) ≈ − |
|
θ1 |
+ θ2 ≈ − n2 |
+ n1 |
|
||||
Если модуль светового вектора падающей волны E — наперед заданная положительная величина, то из равенства (20.6) при условии n2 − n1 > 0 следует, что величина E , которая была введена в рассмотрение как модуль светового вектора отраженной волны, оказывается величиной отрицательной. Однако модуль вектора не может быть отрицательным. Полученное противоречие свидетельствует о том, что первоначальное предположение о том, как направлены векторы E и E (см. рис. 59), было неверным. Для устранения противоречия следует изменить направление вектора E на противоположное. При этом световые векторы E и E оказываются направленными навстречу друг другу, что снова (как и в предыдущем примере) означает скачкообразное изменение фазы волны на величину π при отражении. Таким образом, для двух видов падающей на границу раздела сред световой волны (плоскость колебаний светового вектора параллельна или перпендикулярна плоскости падения) анализ фазовых характеристик падающей и отраженной волн с помощью формул Френеля привел к одному и тому же результату — выводу о скачкообразном изменении фазы волны при отражении света от оптически более плотной среды. Этот результат вполне ожидаемый, так как при почти нормальном падении света на поверхность раздела двух сред рассмотренные два случая расположения плоскости колебаний светового вектора относительно плоскости падения с физической точки зрения становятся по существу неразличимыми.
Закон Брюстера. Пусть световая волна проходит через плоскую поверхность раздела из одной среды с абсолютным показателем преломления n1 в другую cреду с абсолютным показателем преломле-
ния n2.
Углом Брюстера (1781–1868) называется такой угол падения, для которого выполняется соотношение:
tg θБр = |
n2 |
. |
(20.7) |
|
|||
|
n1 |
|
|
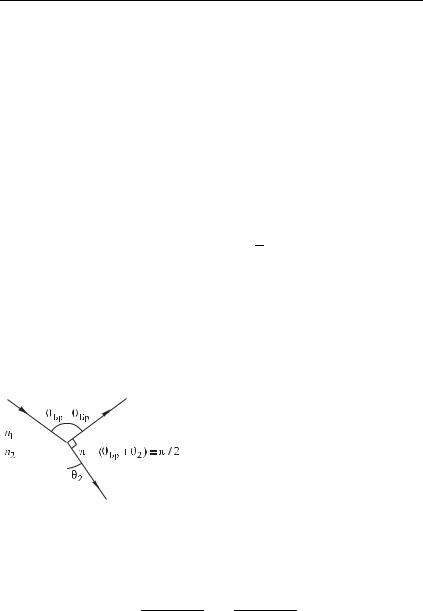
Угол Брюстера обладает следующим свойством: при падении света на поверхность раздела двух сред под углом Брюстера угол между отраженным и преломленным лучами прямой (рис. 60).
4 А. Н. Леденев
98 Введение в оптику [ Гл. IV
Для доказательства утверждения проведем тождественные преобразования и воспользуемся определением (20.7):
tg θБр = |
sin θБр |
= |
|
|
sin θБр |
= |
n2 |
. |
(20.8) |
|||||||
cos θБр |
sin(π/2 − θБр) |
|
||||||||||||||
|
|
|
n1 |
|
||||||||||||
Учтем закон преломления света: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
sin θБр |
= |
n2 |
. |
|
|
|
(20.9) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
sin θ2 |
|
n1 |
|
|
|
|
|||||||
Из уравнений (20.8) и (20.9) находим |
|
|
|
|
||||||||||||
|
|
π |
− θБр = θ2. |
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
||||||||||
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
θБр + θ2 |
= |
π |
, |
|
|
|
(20.10) |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
π
π − (θБр + θ2) = 2 .
Последнее равенство означает, что угол между отраженным и преломленным лучами прямой (см. рис. 60).
Закон Брюстера состоит в следующем. Если угол падения неполяризованного света на плоскую поверхность раздела двух диэлектриков равен углу Брюстера, то отраженная световая волна является плоско поляризованной: плоскость колебаний светового вектора в ней перпендикулярна плоскости падения. Если угол падения отличен
|
|
|
|
от нуля и не равен углу Брюстера, |
|
|
|
|
|
отраженный свет частично поляризо- |
|
|
|
|
|
ван. |
|
|
|
|
|
Всякую световую волну, в част- |
|
|
|
|
|
ности, свет, падающий на границу |
|
|
|
|
|
двух диэлектриков, можно предста- |
|
|
|
|
|
||
|
|
|
|
вить как наложение двух волн, в |
|
|
|
|
|
одной из которых плоскость колеба- |
|
|
|
|
|
ний светового вектора параллельна, |
|
|
|
|
|
в другой — перпендикулярна к плос- |
|
|
Рис. 60 |
кости падения. Применим |
формулу |
||
|
|
|
|
Френеля (20.1) к волне, в |
которой |
световой вектор параллелен плоскости падения, учитывая при этом, что при падении под углом Брюстера выполняется соотношение (20.10) для углов падения θБр и преломления θ2:
E = E |
tg(θБр − θ2) |
= E |
tg(θБр − θ2) |
= 0. |
(20.11) |
|
tg(θБр + θ2) |
|
tg π/2 |
|
|
Из (20.11) следует, что амплитуда светового вектора E в отраженной волне равна нулю, иначе говоря, отраженной волны в этом случае просто не существует, свет, преломляясь, полностью переходит во вторую среду.
§ 20 ] Формулы Френеля. Закон Брюстера 99
Полученный результат (20.11) означает, в частности, что при падении под углом Брюстера параллельного пучка естественного света на границу двух диэлектриков (например, на поверхность стеклянной
пластинки) в отраженном свете будут отсутствовать электромагнитные волны, в которых плоскость колебаний светового вектора параллельна
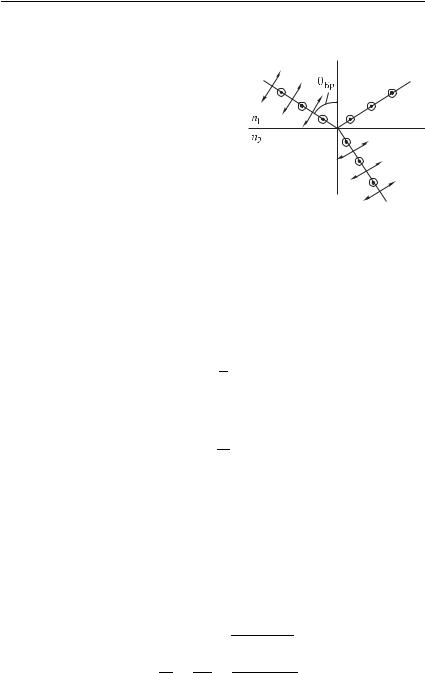
плоскости падения. Отраженный свет окажется полностью поляризованным, причем вектор E перпендикулярен к плоскости падения. Рисунок 61, на котором колебания светового вектора в плоскости падения отмечены стрелками, а в перпендикулярном к этой
плоскости направлении — точками в кружках, иллюстрирует явление поляризации света при отражении.
Коэффициенты отражения и пропускания световой волны.
Пусть свет падает на границу двух диэлектриков.
Коэффициентом отражения ρ называется отношение интенсивности I отраженного света к интенсивности I падающего:
ρ = I .
I
Коэффициентом пропускания τ называется отношение интенсивности I преломленного к интенсивности I падающего света:
τ = I .
I
Как следует из формул Френеля, коэффициенты отражения ρ и ρ света, в котором вектор напряженности электрического поля параллелен и перпендикулярен плоскости падения соответственно, будут различными. То же относится и к коэффициентам пропускания. Вычислим коэффициенты отражения ρ и ρ для указанных двух типов падающего на границу диэлектриков света.
Согласно соотношению (19.2) интенсивность световой волны пропорциональна квадрату амплитуды светового вектора. Используя формулы Френеля (20.1) и (20.3), получим
|
|
|
I |
E |
2 |
2 |
(θ1 − θ2) |
|
|
|
|||||
ρ |
|
= |
|
|
= |
|
|
= |
tg |
, |
(20.12) |
||||
I |
E2 |
|
|||||||||||||
|
|
|
tg2(θ1 + θ2) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
= |
I |
= |
E 2 |
= |
sin2 |
(θ1 |
− θ2) |
. |
(20.13) |
||||
|
|
|
|||||||||||||
|
|
I |
|
E2 |
|
sin2 |
(θ1 |
+ θ2) |
|
||||||
4*
