§ 10 ] Скорость и энергия упругих волн в твердой среде 57

а также вторые производные ξ по координатам x, y и z:

Выразив ξ из правых частей равенств (9.9) и (9.10) и приравняв друг другу полученные выражения, найдем

Уравнение плоской волны (9.7), исходя из которого было выведено волновое уравнение (9.11), является не единственным решением волнового уравнения. Можно показать, что всякая функция вида

f (x, y, z, t) = f (ωt − kr + α),

также является решением волнового уравнения (9.11).

Заметим, что получив тем или иным способом волновое уравнение вида (9.11), можно найти фазовую скорость волны, не решая самого уравнения, а именно: в этом уравнении коэффициент при второй производной по времени смещения ξ частицы представляет собой квадрат величины, обратной фазовой скорости волны V .

§ 10. Скорость и энергия упругих волн в твердой среде

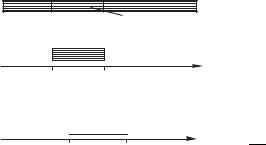
Скорость упругих волн. Пусть продольная плоская волна распространяется в однородной упругой среде в направлении оси x. Например, волна может распространяться в длинном однородном стержне цилиндрической формы из упругого материала в направлении его оси симметрии (рис. 35). Мысленно выделим в стержне малый фрагмент. Обозначим через S площадь поперечного сечения стержня. Координаты двух торцевых поверхностей выделенного фрагмента в положении равновесия (в отсутствие волны) равны x и x + x. Величины сме-

§ 10 ] Скорость и энергия упругих волн в твердой среде 59

Подставив полученное выражение для F1 − F2 в уравнение движения фрагмента (10.1), получим

Выражение (10.2) представляет собой волновое уравнение и описывает распространение плоской волны вдоль оси x. Из него находим скорость упругой продольной волны в твердой среде:

V = Eρ , (10.3)

где E — модуль Юнга, ρ — плотность среды. Подобное выражение легко получить и для поперечной волны. В него вместо модуля Юнга E войдет модуль сдвига G.

Энергия упругих волн. Для вычисления энергии упругой волны выделим в среде, где распространяется волна, малый объем v, масса которого составит величину ρ v, где ρ — плотность вещества среды. Пусть плоская продольная волна распространяется вдоль оси x и описывается уравнением:

ξ = a cos (ωt − kx + α).

где E — модуль Юнга, ∂ξ/∂x — относительная деформация элементарного объема упругой среды. (Выражение (10.5) аналогично выражению для потенциальной энергией деформированной пружины κ (Δl)2/2, где κ — жесткость пружины, l — величина деформации).

Учитывая связь (10.3) модуля Юнга E со скоростью распространения V упругой волны и заменяя V = ω/k, где ω — циклическая частота, k — волновое число, выразим величину E:

2

E = ρV 2 = ρ ω . (10.6) k2

60 Упругие волны [ Гл. II

Подставив (10.6) в (10.5), получим выражение для потенциальной

Полная энергия объема v среды, вовлеченного в волновой процесс, равна сумме кинетической (10.5) и потенциальной (10.7) энергии:

W = Wкин + Wкин = ρ vω2a2 sin2 (ωt − kx + α) .

Объемная плотность энергии упругой волны составит величину

На практике больший интерес представляет не мгновенное (10.8), а среднее по времени значение объемной плотности энергии. Учитывая, что среднее за период колебаний значение функции sin2(ωt − kx + α)

где угловые скобки означают усреднение за время одного преиода колебаний или за большой промежуток времени, включающий огромное количество периодов.

Энергия упругой волны, как следует из (10.8) и (10.9), пропорциональна квадрату амплитуды волны a.

Колебания плотности среды. Пусть в однородной упругой сре-

стержня. Определим, как зависит от времени t и от координаты x плотность материала, из которого изготовлен стержень.

выделенного фрагмента стержня остается неизменной в любой момент времени. Если обозначить через ρ плотность материала стержня в отсутствие волны, ρ (x, t) — плотность материала фрагмента стержня