1976; Заде л. Лиш вистическая переменная. - м., 1972. • 2 в математических моделях лингвистическую переменную в формальном виде представляют следующим

образом: лингвистическая переменная - пятерка (X, Т (X), Ц О, М,), где X — имя неременной, Т(Х) - члены < множества, то есть множество имен лингвистических значений и - область исследования, О - грамматика,

чтобы генерировать имена, и М— множество семантических правил для связи каждого А'со значением.

измерения ее смысла. И действительно, путаница, возникающая при. использовании слов и фраз естественного языка, связана прежде всего с отсутствием ясности, т.е. с неопределенностью, а не со случайностью. Этот тезис является критической точкой для анализа языковых структур и играет важную роль в определении меры достоверности продукционных правил. Таким образом, для измерения неопределенности в нечеткой логике предложена теория возможностей, в то время как теория вероятностей позволяет определить только меру случайности¹.

Другим важным звеном в теории нечетких множеств является нечеткая логика и основанные на ней нечеткие выводы. Основное понятие нечеткой логики — понятие нечеткого предложения (fuzzy proposition), которое определяется как высказывание типа «р: х есть А». Здесь символ х обозначает некоторую физическую величину, например, строгость наказания, измеренную в годах, и т.п., символ А — лингвистическую переменную, которая ассоциируется с нечетким множеством, а символу р — предложение (proposition). Нечеткие предложения комбинируются между собой связками «И», «ИЛИ». Выбор логических связок зависит от смысла и контекста нечетких предложений и взаимосвязи между ними. Нечеткие предложения, соединенные нечетким «И», называют условиями или предпосылками; для их обозначения используют индикатор «ЕСЛИ». Совокупность условий определяет сово­купность выводов, или заключений; для их обозначения используют индикатор «ТОГДА». Совокупность условий и выводов определяет продукционное нечеткое правило (fuzzy rule), а их совокупность в свою очередь образует нечеткую базу правил, которая должна характеризоваться непрерывностью, непротиворечивостью и полнотой². На основе баз правил возможно функционирование нечеткого контроллера принятия решения.

Нечеткие контроллеры — наиболее важное приложение всей нечеткой теории. Их работа сильно отличается от работы стандартных контроллеров; вместо дифференциально-разностных уравнений для описания системы используется экспертное знание. Это знание может быть выражено естественным способом, при помощи лингвистических переменных, описанных размытыми множествами. Все это позволяет выстроить нечеткую систему принятия решений о назначении определенного уголовного наказания, которое с высокой долей вероятности будет соответствовать общественной опасности содеянного виновным лицом. Это возможно в первую очередь потому, что теория нечетких множеств появилась в результате попытки исчисления высказываний с неопределенными лингвистическими переменными, которыми обычно оперирует человек, в том числе и субъект назначения наказания.

Описание механизма построения нечетких систем

Проиллюстрируем сказанное в параграфе некоторыми примерами, позволяющими нам более ясно разобраться в предлагаемом механизме построения нечетких систем применительно к процессу назначения наказания. В классической математике мы в основном используем четкие множества. Для примера: сначала рассмотрим множество X всех вещественных чисел между 0 и 10, которые мы назовем областью исследования. Теперь, давайте определим подмножество X всех вещественных чисел в амплитуде между 5 и 8, определив его как подмножество А, т.е. А = [5,8]. Теперь представим подмножество А с помощью символической функции, т.е. эта функция приписывает число 1 или 0 к каждому элементу в X, в зависимости от того, находится ли элемент в подмножестве А или нет. Это приводит к следующей диаграмме:

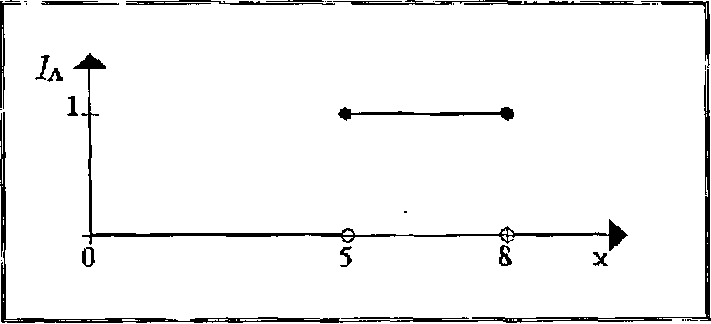
Мы можем интерпретировать элементы, которым назначено число 1, как элементы которые находятся в множестве А и элементы, которым назначено число 0, как элементы не в множестве А. Этой концепции (четких множеств) достаточно для многих областей приложений. Но мы можем легко найти ситуации, где теряется гибкость.

Для чего рассмотрим следующий пример.

В этом примере мы хотим описать небольшой срок наказания в виде лишения свободы, т.е. строгость данного наказания. Более формально можно обозначить В = (небольшой срок наказання в виде лишения свободы}.

Поскольку, в соответствии с ч.2 и 4 ст.56 УК РФ лишение свободы устанавливается на срок от двух месяцев до тридцати лет, нижняя граница этого множества должна быть 2 мес. или ~0,16 года. Верхнюю границу, с другой стороны, надо определить. На первый раз определим верхнюю границу нашего множества, скажем, в 5 лет. Следовательно, мы получаем В как четкий интервал, а именно В = [0.16,5]. Теперь возникает вопрос: почему, скажем срок

наказания в 5 лег считается небольшим, а в 5 лет и 1 день уже не небольшим? Очевидно, это - структурная проблема, поскольку, если мы перемещаем верхнюю границу от 5 до произвольной точки, мы можем излагать тот же самый вопрос. Таким образом, более естественный способ описать множество В состоит в том, чтобы ослабить строгое разделение между «небольшим сроком» и «не небольшим (большим) сроком». Мы будем делать это, допуская не только (четкое) решение «Да» - срок лишения свободы находится в множестве небольших сроков, или «Нет» - срок не в множестве небольших сроков, но более гибких фраз подобно «Хорошо, срок принадлежит немного больше к множеству небольших сроков лишения свободы» или «Нет, срок почти не принадлежит к множеству небольших сроков наказания в виде лишения свободы».

Теперь представим вышеупомянутую идею более формально. В нашем первом примере мы кодировали все элементы области исследования как О («нет») или 1 («есть»/»да»). Прямой путь обобщить эту концепцию состоит в том, чтобы позволить большее количество значений между 0 и 1. Фактически, мы даже позволяем бесконечно многие варианты между 0 и 1, а именно единичный интервал I = [0, 1].

Интерпретация чисел, теперь назначенная всем элементам области исследования, намного более трудная. Конечно, снова число 1 назначено элементу как способ определить элемент который находится в множестве В и О - способ, при котором элемент не определен в множестве В. Все другие значения означают постепенную принадлежность к множеству В. Для большей наглядности, теперь мы показываем множество небольших сроков наказания в виде лишения свободы, подобно нашему первому примеру, графически при помощи символической функции.

5 6 7

срок лишения свободы

1_

0.5.

0,16

10

(в годах)

При таком способе 6-летний срок наказания в виде лишения свободы

будет все еще небольшим сроком на 50 процентов. Таким образом, границы между нечеткими множествами являются размытыми (нечеткими), и переход элементов из одного множества в другое переходит плавно, без скачков. В классической теории множеств этот переход осуществляется скачкообразно и множества имеют четкую границу между собой. Наличие между нечеткими множествами размытых границ как раз и дает возможность их интерпретации в лингвистической форме.

Теперь поставим перед собой другую задачу - интерпретации значений лингвистической переменной «строгость наказания в виде лишения свободы на определенный срок». Представим данную переменную в виде следующих нечетких множеств: «малая (небольшая)», «средняя», «большая»¹. Иными словами, «строгость наказания в виде лишения свободы на определенный срок» = {«малая», «средняя», «большая»}. Для рассматриваемой ЛП «строгость наказания в виде лишения свободы на определенный срок» базовая шкала — это числовая шкала от 2 мес.(=0,16 года) до 30 лет, обозначающая количество возможных к назначению лет наказания. Функция принадлежности В определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории строгости.