12. Моменты инерции сечения. Вычисление моментов инерции брусьев прямоугольного и круглого сечений.

П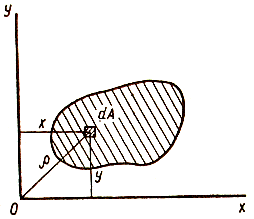редставим, что сечение разделено на множество элементарных площадокdA, координаты которых x и y. Моменты инерции сечения относительно осей x и y: Iх=_(А)∫у²dА, Iу=_(А)∫х²dА. Центробежный момент инерции: Iху=_(А)∫хуdА. Зависимость между осевыми и полярными моментами инерции: Iр=Iх+Iу - сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей. Центральный момент инерции – момент относительно осей, проходящих через центр тяжести сечения.

Прямоугольное сечение имеет 2 оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон. Главный центральный момент инерции относительно оси x: Iх=_(А)∫у²dА. Элементарную площадка dA - полоска во всю ширину сечения толщиной dy, значит dA=b*dy. Проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим: Iх=bh³/12. Аналогично относительно оси y:

Круглое сечение. Для круга главные центральные моменты инерции относительно осей x и y равны между собой: Iх=Iу. Из равенства Iр=Iх+Iу получаем Iр=2Iх=2Iу, I=Ix=Iy=Ip/2, где Iр= πd⁴/32. I=πd⁴/64.

13. Изгиб брусьев. Внутренние силовые факторы в поперечных сечениях бруса и их эпюры. Дифференциальные зависимости при изгибе.

Изгиб– такой вид нагружения, при котором в попереч. сечениях балки возникают изгибающие моменты. Деформация при изгибе – результат поворота сечений на угол φ как единое целое. Верхние слои балки сжимаются, нижние – растягиваются. Сумма элементарных сил от касательных напряжений по площади поперечного сечения изогнутой балки – это внутренняя равнодействующая внутренних поперечных сил Q, действующих по оси Y: Q=∑F_ky. Сумма сил от нормальных напряжений в поперечном сечении характеризует равнодействующий изгибающий момент: М_и=∑Ми(F).

Рассмотрим консольную балку, на которую действует сосредоточенный момент М₀. Условие чистого изгиба: Q=0, M=const, ρ=const. Поперечная сила Q=dM/dx, поперечная нагрузка: q=dQ/dx. М_I=M₀.

Рассмотрим элементарный участок балки с чистым изгибом. Слой АВ получает абсолютное удлинение: ∆l=ВВ₁=∆dx. Из ∆КВВ₁: ∆dx=Y·tgφ=Y·dφ. Из ∆ODК: dx=ρ·tgdφ=ρ·dφ. Относительная деформация: ε=∆dx/dx=Y/ρ. Напряжение при изгибе: σ=Eε=EY/ρ (1). Продольная сила: N=_(S)∫σdS=0; 0=Е/ρ·_(S)∫YdS. Любая площадка на расстоянии Y создает статический момент _(S)∫YdS. Момент М₀ действует в плоскости YOX относительно оси Z. Элементарный момент в поперечном сечении: dM=σ·dS·Y. Мz=Е/ρ·_(S)∫Y²dS, где _(S)∫Y²dS=Iz. Кривизна: 1/ρ=Миz/ЕIz (2), где ЕIz – жесткость при изгибе (зависит от материала, формы попереч. сечения). 1/ρ=dφ/dx, φ=Мl/EIz. (2)->(1): σ/ЕY=Мz/ ЕIz, σ_max=MzY_max/Iz, где Iz/Y_max – момент сопротивления в сечении. σ_max=Mz/Wz.

Правило знаков поперечных сил при изгибе:

Правило знаков изгибающих моментов:

Правило проверки правильности построения эпюр нагружения: в сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.