
- •Расчеты на прочность при сложном сопротивлении
- •2. Косой изгиб
- •2.1. Определение напряжений при косом изгибе
- •2.2. Определение положения нейтральной линии при косом изгибе
- •2.3. Определение перемещений при косом изгибе
- •3. Внецентренное растяжение (сжатие)
- •3.1. Определение напряжений при внецентренном растяжении (сжатии)
- •3.2. Определение положения нейтральной линии
- •3.3 Понятие о ядре сечения
- •4. Совместное действие изгиба и кручения
- •4.1 Расчет брусьев круглого поперечного сечения
- •4.3 Расчет брусьев прямоугольного сечения
- •5. Общий случай сложного сопротивления
- •3. Определение диаметров круглых сечений элементов ломаного бруса при ,.
Министерство
образования Российской Федерации
«МАТИ»-Российский
государственный технологический
университет им. К.Э. Циолковского
Кафедра
«Механика материалов и конструкций»
Методические
указания к выполнению курсовых работ
по курсу «Сопротивление материалов»
Составители:
С. П. Евстратова
Д.В.
Васильев
В.В.
Логвиненко
Москва
2001
Светлана
Павловна Евстратова, к.т.н. доцент
Дмитрий
Владимирович Васильев, к.т.н. доцент
Валерий
Васильевич Логвиненко, к.т.н. доцент
Расчеты
на прочность при сложном сопротивлении
Методические
указания к выполнению лабораторной
работы по курсу «Сопротивление
материалов»
Оригинал-макет
подготовлен:
Ероховым
Николаем Сергеевичем
Редактор
М.А.Соколова
Подписано
в печать 29.05.01.
Обьем
2,75 п.л.
Тираж
75 экз. Заказ 265
109240,
Москва, Берниковская наб., 14.
ИТЦ
МАТИ-РГТУ Введение Под
сложным сопротивлением подразумевают
различные комбинации простейших
деформаций бруса - растяжения или
сжатия, сдвига, кручения и изгиба. При
этом, на основании принципа независимости
действия сил (ПНДС), напряжения и
деформации в стержне при сложном
сопротивлении определяют суммированием
напряжений или деформаций, вызванных
каждым внутренним силовым фактором в
отдельности. Напомним, что этот принцип
применим в тех случаях, когда имеют
место только упругие деформации, а
материал подчиняется закону Гука. Рассмотрение
вопросов, связанных с расчетом на
прочность и жесткость элементов,
работающих в условиях сложного
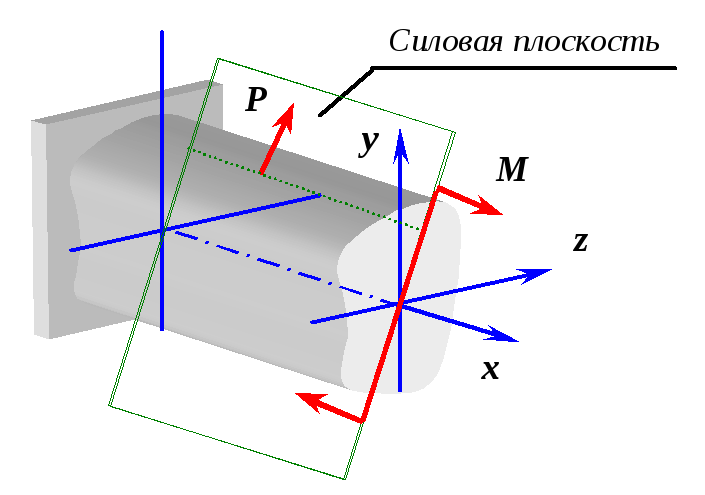
сопротивления, начнем с частных случаев. Изгиб,
при котором внешние нагрузки действуют
в плоскости, не совпадающей ни с одной
из главных плоскостей инерции, называется
косым изгибом (рис.2.1). Главной плоскостью
инерции называется такая плоскость,
которая включает в себя ось балки ( Рассмотрим
консольную балку, нагруженную
сосредоточенной силой как показано на
рис.2.2.
Рис.
2.1 Находим
проекции силы
Каждая
из проекций располагается в одной из
главных центральных плоскостей инерции
и, таким образом, косой изгиб является
сочетанием двух плоских поперечных
изгибов и часто называется двойным.
Рис.
2.2 В
произвольном сечении на расстоянии
поперечные
силы:
и
изгибающие моменты:
Определим
напряжения, возникающие в произвольной
точке
от
изгибающего момента
от
изгибающего момента
здесь
Знак
напряжения зависит от характера
деформации (растяжение-плюс, сжатие-минус).
В нашем случае оба напряжения являются
растягивающими и имеют знак плюс. На
основании ПНДС полное нормальное
напряжение в точке
При
проведении расчетов на прочность
условие прочности составляется для
опасной точки поперечного сечения,
т.е. для точки, в которой нормальные
напряжения достигают максимальных
значений. Самой нагруженной точкой в
сечении произвольной формы является
точка, наиболее удаленная от нейтральной
линии, разделяющей растянутую и сжатую
зоны сечения. В
связи с этим, большое значение приобретают
вопросы, связанные с определением
положения нейтральной линии. Положение
нейтральной линии можно определить с
помощью формулы (2.1), если предположить,
что точка
или
Уравнение
нейтральной линии при косом изгибе
(2.2) есть уравнение прямой, проходящей
через начало координат. Положение
нейтральной линии определяется тангенсом
угла ее наклона
Так
как в общем случае
Из
формулы (2.3) следует, что для сечений с
Определение
положения нейтральной линии позволяет
выявить опасные точки сечения. Для
этого следует построить касательные
к контуру сечения, параллельные
нейтральной линии. Точки касания и
будут являться опасными (точки
Рис.
2.3 Для
некоторых сечений (прямоугольник,
двутавр, швеллер и т.п.) наиболее
напряженные точки расположены в углах
этих сечений, т.е. их можно найти без
определения положения нейтральной
линии (рис.2.4).
Рис.
2.4 Условия
прочности составляют в зависимости от
свойств того материала, из которого
изготовлен элемент конструкции (брус). Для
хрупкого материала используют два
условия прочности - для опасной точки,
где имеет место растяжение (для нашего
случая т.
Необходимость
использования двух условий прочности
для хрупкого материала объясняется
разными механическими свойствами
материала при растяжении и сжатии.
Хрупкий материал плохо сопротивляется
растяжению и хорошо - сжатию. Для
пластичного материала, который одинаково
сопротивляется и растяжению и сжатию,
используют одно условие прочности для
точки поперечного сечения, где имеют
место максимальные по абсолютной
величине нормальные напряжения
где
При
расчетах на прочность касательными
напряжениями от поперечных сил
пренебрегают, т.к. их влияние незначительно. Перемещения
при косом изгибе определяют по принципу
независимости действия сил, т.е.
рассчитывают прогибы
Например,
для балки, изображенной на рис.2.2, прогиб
конца консоли определится следующим
образом:
Рис.
2.5 Направление
полного перемещения (
Сравнивая
выражения (2.6) и (2.3), видим, что
Рассмотрим
примеры расчета балок на косой изгиб. ПРИМЕР
2.1.
Подобрать прямоугольное сечение балки
(рис.2.6) при условии, что
Рис.
2.6 Решение:
Разложив силу
следовательно,
это сечение является опасным.
Рис.
2.7 Для
определения положения опасной точки
расставим знаки от
Судя
по условию задачи, материал, из которого
изготовлена балка, является пластичным
(
Вычислим
моменты сопротивления сечения при
заданном соотношении высоты и ширины
Подставляя
в условие прочности выражения для
изгибающих моментов и моментов
сопротивления, получим:
тогда
ПРИМЕР
2.2.
При установке на опоры двутавровой
балки (№ 60:
Рис.
2.8 Решение:
Отклонение оси двутавра (ось
Максимальные
напряжения при косом изгибе
так
как
В
случае правильной установки балки,
сила
Таким
образом, максимальные напряжения при
косом изгибе за счет такого незначительного
отклонения от вертикали возрастут на
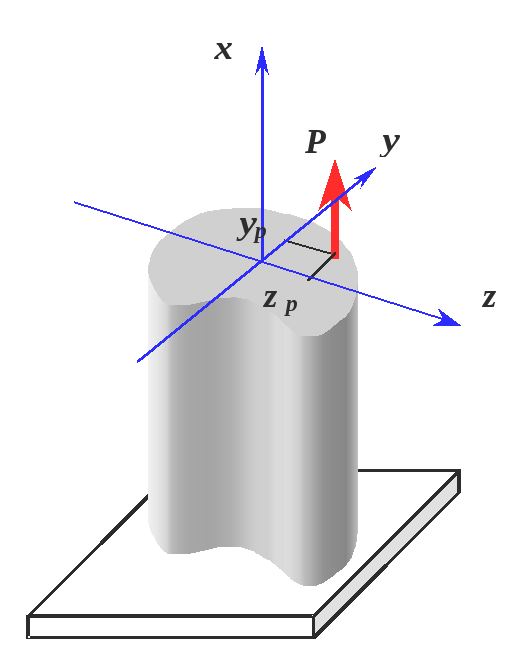
24,6 %. Вид
деформации, при котором точка приложения
продольной силы не совпадает с центром
тяжести сечения, называется внецентренным
растяжением или сжатием (рис.3.1).
Здесь
Рис.
3.1 Для
определения внутренних усилий, в
поперечных сечениях бруса при
внецентренном растяжении (сжатии)
заменим заданную систему сил на
статически эквивалентную систему
других сил. На основании принципа
Сен-Венана такая замена не вызовет
изменений в условиях нагружения и
деформации частей бруса, достаточно
удаленных от места приложения сил. Сначала
перенесем точку приложения силы
Рис.
3.2 Таким
образом, действие силы
Пользуясь
методом сечений, нетрудно установить,
что во всех поперечных сечениях
внецентренно растянутого (сжатого)
бруса действуют следующие внутренние
силовые факторы: продольная сила
Рис.
3.3 Напряжения
в поперечных сечениях бруса определим,
используя принцип независимости
действия сил. От всех внутренних силовых
факторов в поперечных сечениях возникают
нормальные напряжения. Знаки напряжений
устанавливают по характеру деформаций:
плюс - растяжение, минус - сжатие.
Расставим знаки напряжений от каждого
из внутренних силовых факторов в точках
Полное
напряжение в точке
Самой
нагруженной точкой в сечении произвольной
формы является точка, наиболее удаленная
от нейтральной линии. В связи с этим,
большое значение приобретают вопросы,
связанные с определением положения
нейтральной линии. Положение
нейтральной линии можно определить с
помощью формулы (3.1), приравняв нормальные
напряжения нулю
здесь
Последнее
выражение можно преобразовать, используя
формулы для радиусов инерции:
или
Из
уравнения (3.2) видно, что нейтральная
линия при внецентренном растяжении
(сжатии) - это прямая, не проходящая
через начало координат (центр тяжести
поперечного сечения). Проведем
эту прямую через две точки, лежащие на
координатных осях (рис. 3.4). Пусть точка
1 лежит на оси
Если
координаты
Определения
положения нейтральной линии позволяет
выявить опасные точки сечения, т.е.
точки, в которых нормальные напряжения
принимают наибольшие значения. Для
этого следует построить касательные
к контуру сечения, параллельные
нейтральной линии. Точки касания
Рис.
3.4 Условия
прочности для опасных точек составляют
в зависимости от свойств того материала,
из которого изготовлен брус. Так как
хрупкий материал обладает различными
свойствами в условиях растяжения и
сжатия – плохо сопротивляется растяжению
и хорошо сжатию, условия прочности
составляют для двух точек: где действуют
максимальные растягивающие (т.
Для
пластичного материала, который одинаково
сопротивляется и растяжению и сжатию,
составляют одно условие прочности для
точки поперечного сечения, где имеют
место максимальные по абсолютной
величине нормальные напряжения. В нашем
случае такой точкой является точка
При
построении нейтральной линии (рис. 3.4)
определялись координаты точек 1 и 2,
через которые она и проводилась т.
1:
(3.5) т.
2:
Координаты
точек, лежащих на нейтральной линии,
зависят от положения точки приложения
силы (полюса) с координатами
Область
приложения продольных сил, которые в
этом случае вызывают в поперечном
сечении напряжения одного знака,
называется ядром
сечения. Вопрос
определения ядра сечения является
наиболее актуальным для элементов
конструкций из хрупкого материала,
работающих на внецентренное сжатие, с
целью получения в поперечном сечении
только сжимающих напряжений, т.к. хрупкий
материал плохо сопротивляется деформации
растяжения. Для этого необходимо
задаться рядом положений нейтральной
линии, проводя ее через граничные точки
контура, и вычислить координаты
соответствующих точек приложения силы,
по формулам, вытекающим из (3.5). Геометрическое
место рассчитанных таким образом точек
и определит контур ядра сечения. На
рис. 3.6 показаны примеры ядра сечения
для распространенных форм.
Рис.
3.5
Рассмотрим
пример расчетов на внецентренное
растяжение-сжатие. Пример
3.1.
Стальная полоса шириной
Рис.
3.6 Решение.
При несимметричной прорези центр
тяжести ослабленного сечения смещается
от линии действия силы вправо и возникает
внецентренное растяжение. Для определения
положения центра тяжести (
В
этом случае в поперечном сечении
С
целью определения опасной точки
расставим знаки напряжений по боковым
сторонам поперечного сечения (рис.
3.6). От продольной силы во всех точках
сечения имеют место положительные
(растягивающие) напряжения. От изгибающего
момента слева от оси
Таким
образом, максимальные нормальные
напряжения возникают в т.
где
В
результате максимальные нормальные
напряжения будут равны
При
симметричной прорези шириной
тогда
На
практике деформации кручения часто
сопутствует изгиб. Например совместное
действие изгиба с кручением приходится
учитывать при расчете валов машин,
испытывающих воздействие окружных и
радиальных усилий. Сочетание изгиба с
кручением имеет место в пространственных
рамах, коленчатых валах и других
элементах конструкций. В
предыдущих разделах рассматривались
такие частные случаи сложного
сопротивления (косой изгиб, внецентренное
растяжение или сжатие), при которых в
поперечных сечениях бруса возникали
только нормальные напряжения, и,
следовательно, имело место одноосное
напряженное состояние. Это позволило
при выводе расчетных формул использовать
сечения произвольной формы. В
случае изгиба с кручением от крутящего
момента в поперечных сечениях бруса
возникают касательные напряжения,
которые рассчитываются по разному для
круглых и прямоугольных брусьев. В
следствие этого, рассматривать расчет
сечений произвольной формы не
представляется возможным. Пусть
в поперечном сечении круглого бруса
(рис. 4.1) действуют два изгибающих момента
Максимального
значения нормальные напряжения от
Кроме
того, в поперечном сечении бруса имеет
место крутящий момент (
Рис.
4.1 В
т.
причем
осевой
Проанализируем
напряжения в т.
Рис.
4.2 Как
видно из рис. 4.2, в данном случае имеет
место плоское напряженное состояние
и расчет на прочность должен вестись
по одной из гипотез прочности. Для
пластичных материалов применяют
гипотезу наибольших касательных
напряжений (III)
или энергетическую гипотезу (IV). Условие
прочности по III
гипотезе записывается в виде
В
рассматриваемом случае
или
где
Условие
прочности по IV
гипотезе прочности записывается в виде
В
рассматриваемом случае
или
где
Для
хрупких материалов может быть использована
гипотеза прочности Мора, которая для
пластичных материалов приводится к
третьей гипотезе, а для очень хрупких
– к первой гипотезе
Аналогичный
расчет проводится и для кольцевого
сечения. Пример
4.1.
Стальной вал круглого поперечного
сечения передает мощность
Решение.
Условие прочности при одновременном
действии изгиба и кручения по III
гипотезе прочности
Находим
величину передаваемого валом крутящего
момента
Эквивалентный
момент по третьей гипотезе прочности
равен
а
диаметр вала
или
Условие
прочности при одновременном действии
изгиба и кручения по IV
гипотезе прочности Эквивалентный
момент по четвертой гипотезе прочности
равен
а
диаметр вала
или
Таким
образом, расчет по энергетической
теории прочности дал более экономичный
размер сечения, чем по критерию наибольших
касательных напряжений.
Рассмотрим
брус прямоугольного сечения, нагруженный
таким образом, что в его поперечных
сечениях действуют изгибающие моменты
Рис.
4.3 Чтобы
проверить прочность бруса, нужно в
опасном сечении найти опасную точку,
вычислить для нее эквивалентное
напряжение (по одной из теорий прочности)
и сопоставить его с допускаемым
напряжением. Для
нахождения опасной точки сечения
построим эпюры напряжений от всех
силовых факторов (рис. 4.4).
Рис.
4.4 Эпюры
нормальных и касательных напряжений
наглядно показывают, что, в отличие от
круглого сечения, точки, в которых имеют
место максимальные нормальные и
максимальные касательные напряжения,
не совпадают. В следствие этого, условие
прочности составляют, как минимум для
трех наиболее опасных точек поперечного
сечения. Опасной
точкой по нормальным напряжениям
является точка
Опасной
точкой по касательным напряжениям
является точка
Следует
отметить, что в точке
Таким
образом, в точках поперечного сечения
Составим
условия прочности для трех предположительно
опасных точек поперечного сечения
т.
т.
т.
Расчетная
формула по четвертой гипотезе прочности
Для
хрупких материалов может быть использована
гипотеза прочности Мора, которая для
пластичных материалов приводится к
третьей гипотезе, а для очень хрупких
– к первой гипотезе
Пример
4.2.
Коленчатый стальной стержень
прямоугольного поперечного сечения
защемлен одним концом и нагружен
поперечной силой
Рис.
4.5 Решение:
Построим эпюру моментов с целью
определения величин внутренних силовых
факторов, действующих в поперечном
сечении стержня в заделке (рис. 4.6).
Рис.
4.6 В
результате действия силы
Эквивалентные
напряжения по третьей теории прочности
рассчитываются по формуле
Для
точки
здесь
Для
точки
здесь
Приемы
определения напряжений и деформаций,
которые использовались при решении
частных задач сложного сопротивления
(косой изгиб, внецентренное
растяжение-сжатие, изгиб с кручением)
могут быть распространены на более
сложные случаи нагружения, когда в
поперечных сечениях бруса действуют
все шесть силовых факторов. В
качестве примера рассмотрим расчет
ломанного бруса, показанного на рис.
5.1. Пример
5.1.
Для заданного ломанного бруса (рис.
5.1), имеющего круглые поперечные сечения
в пределах элементов длиной
Рис.
5.1 1.
Построить эпюры продольных усилий,
изгибающих и крутящих моментов, 2.
Определить допускаемые нагрузки
3.
Определить диаметры круглых сечений
элементов бруса длиной
Примечания: а)
Построение эпюр внутренних силовых
факторов производить, используя
скользящую систему координат с постоянным
направлением осей. б)
В расчетах на прочность использовать
теорию максимальных касательных
напряжений. в)
Прямоугольное сечение бруса длиной
Таблица
исходных значений
0.23
0.28
0.33
1.3
3
2.5
160
Решение.
1.
Построение эпюр внутренних силовых
факторов Для
определения величины и характера
распределения внутренних силовых
факторов по длине каждого участка
ломаного бруса построим эпюры продольных
сил
Рис.
5.2 2.
Определение допускаемой нагрузки
2.1
Определение опасного сечения элемента
бруса длиной
Анализ
эпюр показывает, что наиболее опасным
является сечение в заделке. В этом
сечении действуют: максимальный
изгибающий момент
2.2
Определение опасных точек в опасном
сечении элемента Прямоугольное
сечение элемента бруса длиной
Максимальный
изгибающий момент также действует
относительно оси
Для
определения положения опасных точек
в опасном сечении построим эпюры
распределения нормальных (от
Рис.
5.3 Эпюры
нормальных и касательных напряжений
показывают, что наиболее опасными
являются следующие три точки этого
сечения: точка
точка
точка
2.3.
Определение величин изгибающих и
крутящих моментов в опасном сечении и
моментов сопротивления. Выразим
Моменты
в опасном сечении имеют следующие
значения:
При
заданном соотношении
где
при
2.4
Определение допускаемой нагрузки Расчет
в точке
.
Расчет
в точке
Так
как в точке
Расчет
в точке
где
По
III
гипотезе прочности имеем
Из
полученных результатов видно, что
сосредоточенная сила
3.1.
Определение диаметра круглого сечения
элемента бруса длиной
Опасным
является сечение в конце участка, если
двигаться от свободного конца бруса,
где действует один силовой фактор –
изгибающий момент
3.2.
Определение диаметра круглого сечения
элемента бруса длиной
Анализ
эпюр (рис. 5.2) на втором участке показывает,
что опасным является сечение в конце
участка, если двигаться со свободного
конца бруса, где изгибающие моменты
Рис.
5.4 Величины
моментов
Условие
прочности для круглого сечения согласно
III
теории прочности имеет вид
где

Расчеты на прочность при сложном сопротивлении
2. Косой изгиб
![]() )
и одну из главных центральных осей
инерции поперечного сечения (
)
и одну из главных центральных осей
инерции поперечного сечения (![]() или
или![]() ).
Плоскость, в которой располагаются
внешние нагрузки, называется силовой
плоскостью.
).
Плоскость, в которой располагаются
внешние нагрузки, называется силовой
плоскостью.2.1. Определение напряжений при косом изгибе
![]() на главные центральные оси инерции
на главные центральные оси инерции![]() и
и![]() (рис.2.2):
(рис.2.2):![]() и
и
![]() .
.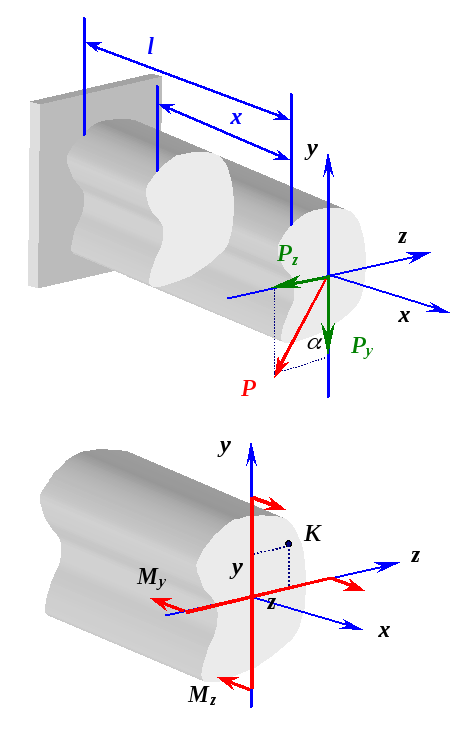
![]() от точки приложения силы имеют место
четыре внутренних силовых фактора:
от точки приложения силы имеют место
четыре внутренних силовых фактора:![]() ,
,![]() ;
;![]() ,
,![]() .
.![]() рассматриваемого сечения (рис.2.2):
рассматриваемого сечения (рис.2.2):![]()
![]() ,
,![]()
![]() ,
,![]() и
и![]() - координаты точки, в которой рассчитывают
напряжения.
- координаты точки, в которой рассчитывают
напряжения.![]() равно их алгебраической сумме:
равно их алгебраической сумме:![]() . (2.1)
. (2.1)2.2. Определение положения нейтральной линии при косом изгибе
![]() с координатами
с координатами![]() лежит на нейтральной линии. В этом
случае нормальное напряжение в точке
равно нулю
лежит на нейтральной линии. В этом
случае нормальное напряжение в точке
равно нулю![]() ,
,![]()
![]() . (2.2)
. (2.2)![]() (рис.2.3) к главной оси
(рис.2.3) к главной оси![]() .
С учетом (2.2) находим
.
С учетом (2.2) находим![]() ,
,![]() ,
,
![]() . (2.3)
. (2.3)![]() и, следовательно,
и, следовательно,![]() ,
то можно заключить, что при косом изгибе
нейтральная линия не перпендикулярна
к линии действия внешней силы.
,
то можно заключить, что при косом изгибе
нейтральная линия не перпендикулярна
к линии действия внешней силы.![]() (квадрат, круг, кольцо, правильный
многоугольник), т.е. для сечений, у
которых любые центральные оси являются
главными, углы
(квадрат, круг, кольцо, правильный
многоугольник), т.е. для сечений, у
которых любые центральные оси являются
главными, углы![]() и
и![]() равны, и нейтральная линия перпендикулярна
линии действия внешней силы. Балки
такого сечения не испытывают деформации
косого изгиба.
равны, и нейтральная линия перпендикулярна
линии действия внешней силы. Балки
такого сечения не испытывают деформации
косого изгиба.![]() и
и![]() на рис.2.3).
на рис.2.3).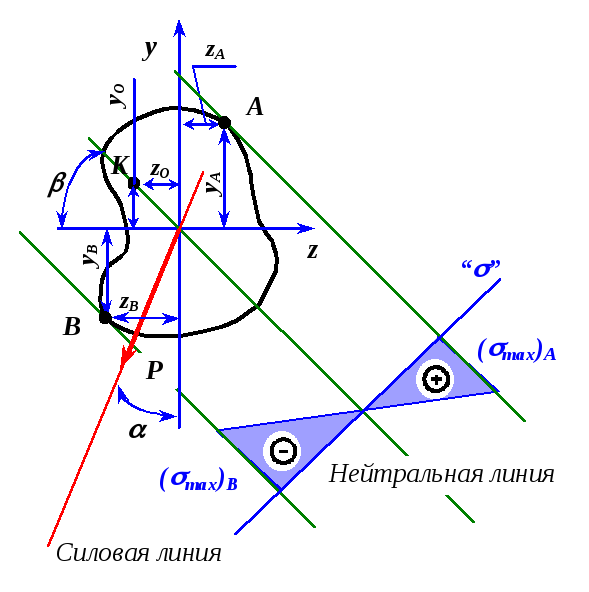

![]() на рис.2.3), и для точки, где имеет место
сжатие (т.
на рис.2.3), и для точки, где имеет место
сжатие (т.![]() )
) (2.4)
(2.4)![]() (2.5)
(2.5)![]() и
и![]() - координаты данной точки.
- координаты данной точки.2.3. Определение перемещений при косом изгибе
![]() и
и![]() в направлении главных осей, а величину
полного прогиба в любом сечении балки
получают геометрическим суммированием:
в направлении главных осей, а величину
полного прогиба в любом сечении балки
получают геометрическим суммированием:![]() .
.![]() ,
,![]() ,
,![]() .
.
![]() )
определится величиной отношения
)
определится величиной отношения
![]() (рис.2.5)
(рис.2.5)![]() . (2.6)
. (2.6)![]() ,
т.е. направление полного прогиба при
косом изгибе перпендикулярно нейтральной
линии и не совпадает с направлением
внешней силы (рис.2.5.).
,
т.е. направление полного прогиба при
косом изгибе перпендикулярно нейтральной
линии и не совпадает с направлением
внешней силы (рис.2.5.).![]() ,
,![]() =160
МПа,
=160
МПа,![]() .=60
кН,
.=60
кН,![]() =30,
=30,
![]() =2.8
м.
=2.8
м.
![]() на две составляющие, действующие по
направлению главных осей поперечного
сечения балки, определяем опорные
реакции и строим эпюры изгибающих
моментов
на две составляющие, действующие по
направлению главных осей поперечного
сечения балки, определяем опорные
реакции и строим эпюры изгибающих
моментов![]() и
и![]() (рис.2.7). Наибольшие моменты действуют
в среднем сечении, где
(рис.2.7). Наибольшие моменты действуют
в среднем сечении, где![]() ,
, ![]() ,
,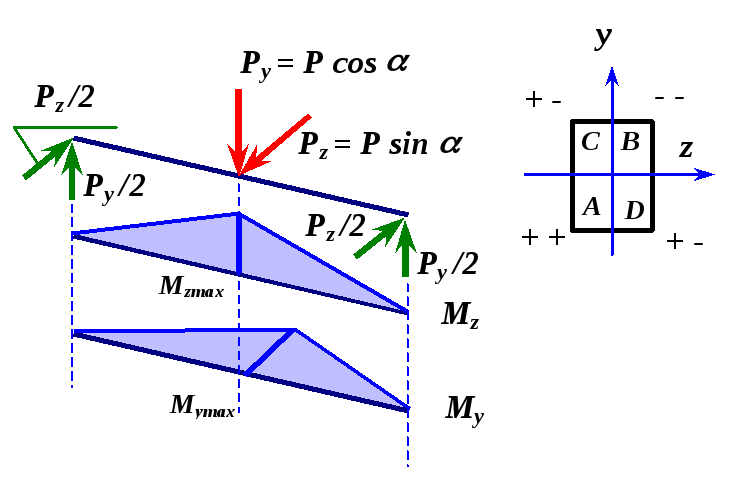
![]() и
и![]() в угловых точках поперечного сечения
балки (рис.2.7).При действии момента
в угловых точках поперечного сечения
балки (рис.2.7).При действии момента![]() в точках
в точках![]() и
и![]() будут иметь место положительные
(растягивающие) напряжения, а в точках
будут иметь место положительные
(растягивающие) напряжения, а в точках![]() и
и![]() - отрицательные (сжимающие) напряжения.
При действии момента
- отрицательные (сжимающие) напряжения.
При действии момента![]() в точках
в точках![]() и
и![]() будут иметь место положительные
будут иметь место положительные![]() ,
а в точках
,
а в точках![]() и
и![]() - отрицательные. Точки поперечного
сечения
- отрицательные. Точки поперечного
сечения![]() и
и![]() ,
в которых действуют нормальные напряжения
одного знака, являются опасными; для
них и должны составляться условия
прочности.
,
в которых действуют нормальные напряжения
одного знака, являются опасными; для
них и должны составляться условия
прочности.![]() =160
МПа) и, следовательно, одинаково
сопротивляется деформации растяжения
и деформации сжатия. Таким образом,
точки
=160
МПа) и, следовательно, одинаково
сопротивляется деформации растяжения
и деформации сжатия. Таким образом,
точки![]() и
и![]() являются равноопасными, и для них
используется одно условие прочности
(2.5)
являются равноопасными, и для них
используется одно условие прочности
(2.5)![]() .
.![]() ,
, ![]() .
.![]() ,
,![]() =18,04
см.
=18,04
см.![]() =182см3,
=182см3,
![]() =2560см3),предназначенной
для работы на изгиб в вертикальной
плоскости, совпадающей с плоскостью
стенки, была допущена ошибка и стенка
двутавра отклонилась от вертикали на
угол
=
1о.
Определить связанное с этим увеличение
наибольших нормальных напряжений.
=2560см3),предназначенной
для работы на изгиб в вертикальной
плоскости, совпадающей с плоскостью
стенки, была допущена ошибка и стенка
двутавра отклонилась от вертикали на
угол
=
1о.
Определить связанное с этим увеличение
наибольших нормальных напряжений.
![]() )
от вертикали привело к возникновению
косого изгиба (рис.2.8) и появлению
изгибающих моментов
)
от вертикали привело к возникновению
косого изгиба (рис.2.8) и появлению
изгибающих моментов![]() и
и![]()
![]() ,
,![]() .
.![]() ,
,![]()
![]() ,
то
,
то![]() .
.![]() совпадала бы с вертикальной осью балки
совпадала бы с вертикальной осью балки![]() ,
и имел бы место прямой изгиб, изгибающий
момент был бы равен
,
и имел бы место прямой изгиб, изгибающий
момент был бы равен![]() (см.рис.2.8), а напряжения
(см.рис.2.8), а напряжения![]() .
.3. Внецентренное растяжение (сжатие)
![]() ,
,![]() - координаты точки приложения силы
- координаты точки приложения силы![]() в системе главных центральных осей
инерции
в системе главных центральных осей
инерции![]() и
и![]() .
.
3.1. Определение напряжений при внецентренном растяжении (сжатии)
![]() на ось
на ось![]() и приложим в этой точке силу, равную
силе
и приложим в этой точке силу, равную
силе![]() ,
но противоположно направленную
(рис.3.2). Чтобы оставить силу
,
но противоположно направленную
(рис.3.2). Чтобы оставить силу![]() на оси
на оси![]() ,
к ее действию необходимо добавить
действие пары сил, отмеченных двумя
чертами, или момент
,
к ее действию необходимо добавить
действие пары сил, отмеченных двумя
чертами, или момент![]() .
Далее перенесем силу
.
Далее перенесем силу![]() в центр тяжести сечения и в этой точке
приложим силу, равную силе
в центр тяжести сечения и в этой точке
приложим силу, равную силе![]() ,
но противоположно направленную
(рис.3.2). Чтобы оставить силу
,
но противоположно направленную
(рис.3.2). Чтобы оставить силу![]() в центре тяжести, к ее действию необходимо
добавить еще одну пару сил, отмеченных
крестиками, или момент
в центре тяжести, к ее действию необходимо
добавить еще одну пару сил, отмеченных
крестиками, или момент![]() .
.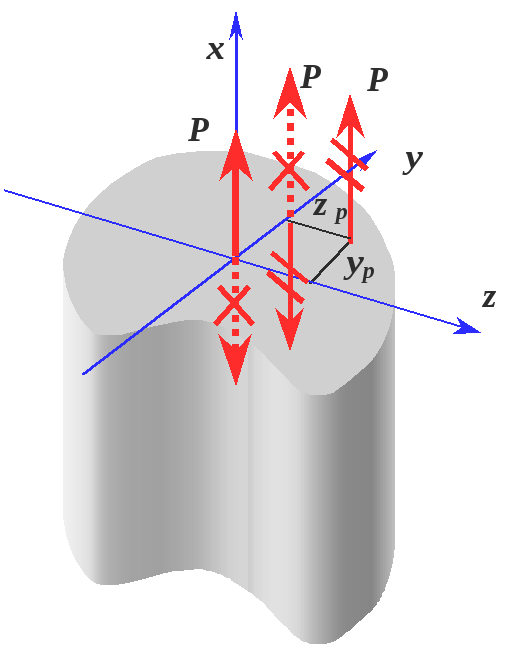
![]() ,
приложенной к сечению внецентренно,
эквивалентно совместному действию
центрально приложенной силы
,
приложенной к сечению внецентренно,
эквивалентно совместному действию
центрально приложенной силы![]() и двух внешних сосредоточенных моментов
и двух внешних сосредоточенных моментов![]() и
и![]() .
.![]() и два изгибающих момента
и два изгибающих момента![]() и
и![]() (рис.3.3).
(рис.3.3).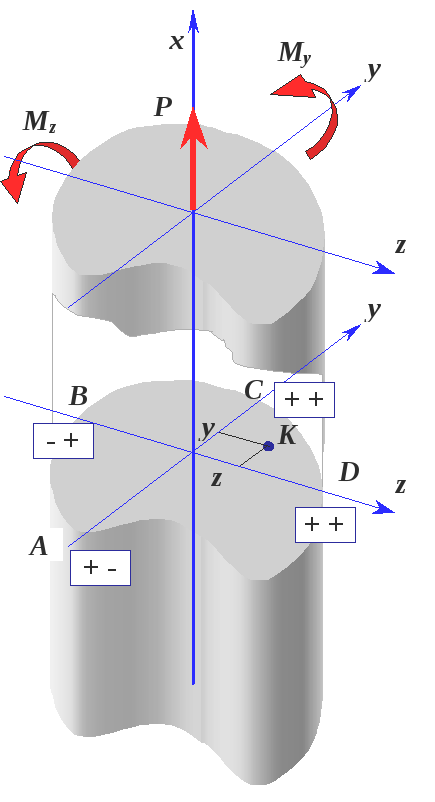
![]() ,
,![]() ,
,![]() ,
,![]() пересечения осей
пересечения осей![]() и
и![]() с контуром поперечного сечения (рис.3.3).
От продольной силы
с контуром поперечного сечения (рис.3.3).
От продольной силы![]() во всех точках сечения
во всех точках сечения![]() одинаковы и положительны; от момента
одинаковы и положительны; от момента![]() в точке
в точке![]() напряжения - плюс, в точке
напряжения - плюс, в точке![]() - минус, в точках
- минус, в точках![]() и
и![]()
![]() ,
т.к. ось
,
т.к. ось![]() является в этом случае нейтральной
линией; от момента
является в этом случае нейтральной
линией; от момента![]() в точке
в точке![]() напряжения - плюс, в точке
напряжения - плюс, в точке![]() - минус, в точках
- минус, в точках![]() и
и![]()
![]() ,
т.к. ось
,
т.к. ось![]() в этом случае является нейтральной
линией.
в этом случае является нейтральной
линией.![]() с координатами
с координатами![]() и
и![]() ,
будет равно:
,
будет равно:![]() (3.1)
(3.1)3.2. Определение положения нейтральной линии
![]() ,
,![]() и
и![]() - координаты точки, лежащей на нейтральной
линии.
- координаты точки, лежащей на нейтральной
линии.![]() и
и![]() .
Тогда
.
Тогда ,
,![]() . (3.2)
. (3.2)![]() ,
тогда ее координатами будет
,
тогда ее координатами будет![]() и
и![]() ,
а точка 2 – на оси
,
а точка 2 – на оси![]() ,
тогда ее координатами будет
,
тогда ее координатами будет![]() и
и![]() (на основании уравнения (3.2)).
(на основании уравнения (3.2)).![]() точки приложения силы (полюса)
положительны, то координаты точек 1 и
2 отрицательны, и наоборот. Таким образом,
полюс и нейтральная линия располагаются
по разные стороны от начала координат.
точки приложения силы (полюса)
положительны, то координаты точек 1 и
2 отрицательны, и наоборот. Таким образом,
полюс и нейтральная линия располагаются
по разные стороны от начала координат.![]() и
и![]() будут являться опасными (рис. 3.4).
будут являться опасными (рис. 3.4).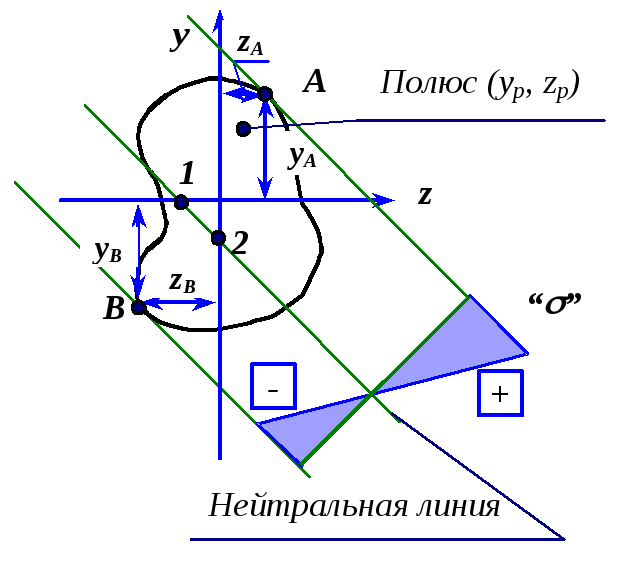
![]() )
и максимальные сжимающие (т.
)
и максимальные сжимающие (т.![]() )
напряжения (рис. 3.4)
)
напряжения (рис. 3.4) (3.3)
(3.3)![]() ,
в которой действуют напряжения одного
знака
,
в которой действуют напряжения одного
знака![]() . (3.4)
. (3.4)3.3 Понятие о ядре сечения
![]() ;
;![]() ,
,![]() ;
;![]() .
.![]() .
Если координаты полюса уменьшаются,
т.е. полюс приближается к центру тяжести
сечения, то
.
Если координаты полюса уменьшаются,
т.е. полюс приближается к центру тяжести
сечения, то![]() увеличиваются, т.е. нейтральная линия
может выйти за пределы сечения или
касаться контура сечения. В этом случае
в сечении будут иметь место напряжения
одного знака.
увеличиваются, т.е. нейтральная линия
может выйти за пределы сечения или
касаться контура сечения. В этом случае
в сечении будут иметь место напряжения
одного знака.
![]() =10
см и толщиной
=10
см и толщиной![]() =1
см, центрально растянутая силами
=1
см, центрально растянутая силами![]() =70
кН, имеет прорезь шириной
=70
кН, имеет прорезь шириной![]() =3
см (рис. 3.6). Определить наибольшие
нормальные напряжения в сечении
=3
см (рис. 3.6). Определить наибольшие
нормальные напряжения в сечении![]() ,
не учитывая концентрации напряжений.
Какой ширины
,
не учитывая концентрации напряжений.
Какой ширины![]() могла бы быть прорезь при той же величине
растягивающего усилия, если бы она была
расположена посередине ширины полосы?
могла бы быть прорезь при той же величине
растягивающего усилия, если бы она была
расположена посередине ширины полосы?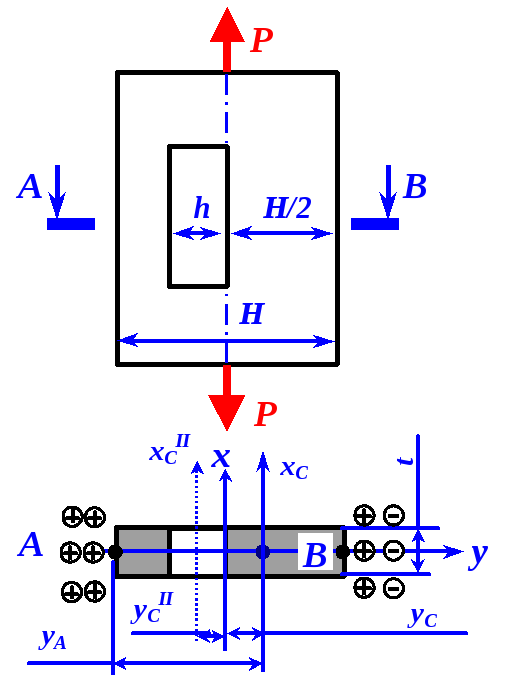
![]() )
ослабленное сечение представим как
большой прямоугольник размерами
)
ослабленное сечение представим как
большой прямоугольник размерами![]() (фигураI)
из которого удален малый прямоугольник
с размерами
(фигураI)
из которого удален малый прямоугольник
с размерами
![]() (фигураII).
За исходную ось примем ось
(фигураII).
За исходную ось примем ось
![]() .
. .
.![]() возникает два внутренних силовых
фактора: продольная сила
возникает два внутренних силовых
фактора: продольная сила![]() и изгибающий момент
и изгибающий момент![]() .
.![]() имеют место растягивающие напряжения
(знак плюс), справа – сжимающие (знак
минус).
имеют место растягивающие напряжения
(знак плюс), справа – сжимающие (знак
минус).![]()
 ,
,![]() - площадь ослабленного сечения, равная
- площадь ослабленного сечения, равная![]() =7
см2;
=7
см2;
![]() -
момент инерции ослабленного сечения
относительно главной центральной оси
-
момент инерции ослабленного сечения
относительно главной центральной оси
![]()

![]() -
расстояние от нейтральной линии (
-
расстояние от нейтральной линии (![]() )
до наиболее удаленной точки (т.
)
до наиболее удаленной точки (т.![]() )
)![]() .
.![]() .
.![]() возникает только растяжение
возникает только растяжение![]() ,
,![]() .
.4. Совместное действие изгиба и кручения
4.1 Расчет брусьев круглого поперечного сечения
![]() и
и![]() ,
которые могут быть приведены к одному
суммарному моменту
,
которые могут быть приведены к одному
суммарному моменту![]() ,
т.к. все центральные оси круга являются
главными
,
т.к. все центральные оси круга являются
главными![]() . (4.1)
. (4.1)![]() достигают в т.
достигают в т.![]() (положительные
(положительные![]() ),
или в т.
),
или в т.![]() (отрицательные
(отрицательные![]() ).
Знаки напряжений устанавливают по
характеру деформаций.
).
Знаки напряжений устанавливают по
характеру деформаций.![]() )
(рис. 4.1). Максимального значения
касательные напряжения от
)
(рис. 4.1). Максимального значения
касательные напряжения от![]() достигают в точках на контуре сечения.
Следовательно, т.
достигают в точках на контуре сечения.
Следовательно, т.![]() (или т.
(или т.![]() )
является опасной, для которой и
составляется условие прочности.
)
является опасной, для которой и
составляется условие прочности.
![]() имеют место напряжения
имеют место напряжения (4.2)
(4.2)![]() и полярный
и полярный![]() моменты сопротивления для круглого
сечения рассчитываются по формулам
моменты сопротивления для круглого
сечения рассчитываются по формулам (4.3)
(4.3)![]() .
С этой целью вырежем в окрестностях
этой точки элементарный параллелепипед,
передняя грань которого совпадает с
поперечным сечением бруса (рис. 4.2).
.
С этой целью вырежем в окрестностях
этой точки элементарный параллелепипед,
передняя грань которого совпадает с
поперечным сечением бруса (рис. 4.2).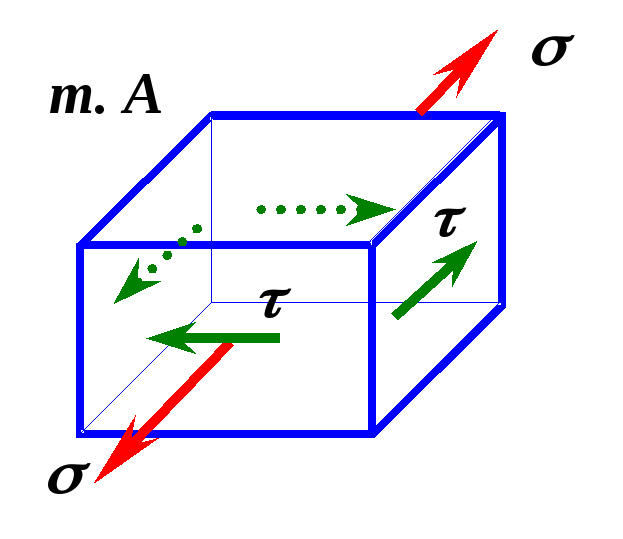
![]() . (4.4)
. (4.4)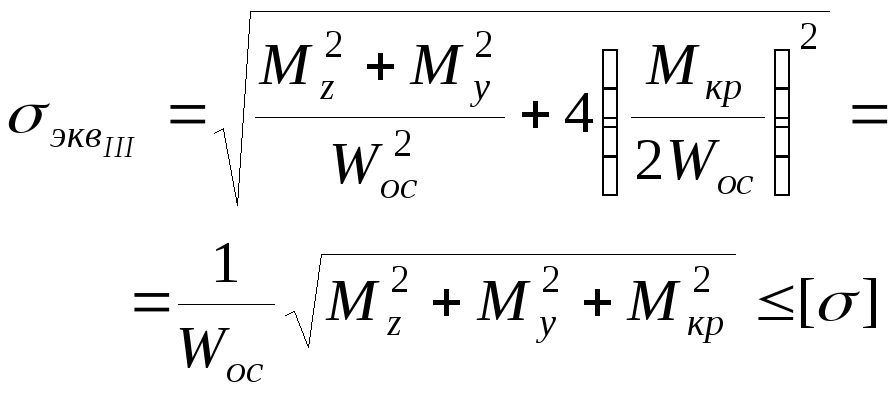 ,
,![]() , (4.5)
, (4.5)![]() - эквивалентный момент по третьей
гипотезе прочности.
- эквивалентный момент по третьей
гипотезе прочности.![]() . (4.6)
. (4.6) ,
,![]() , (4.7)
, (4.7)![]() - эквивалентный момент по четвертой
гипотезе прочности.
- эквивалентный момент по четвертой
гипотезе прочности.![]() . (4.7)
. (4.7)![]() =14.7
кВт при угловой скорости
=14.7
кВт при угловой скорости![]() =10.5
рад/с. Величина наибольшего изгибающего
момента, действующего на вал
=10.5
рад/с. Величина наибольшего изгибающего
момента, действующего на вал![]() =1.5
кНм. Исходя из условий прочности поIII
и IV
теориям прочности, определить необходимый
диаметр вала, если
=1.5
кНм. Исходя из условий прочности поIII
и IV
теориям прочности, определить необходимый
диаметр вала, если
![]() =80
МПа.
=80
МПа.![]() .
.![]() .
.![]() ,
, ,
,![]() =63.5
мм.
=63.5
мм.![]() .
.![]() ,
,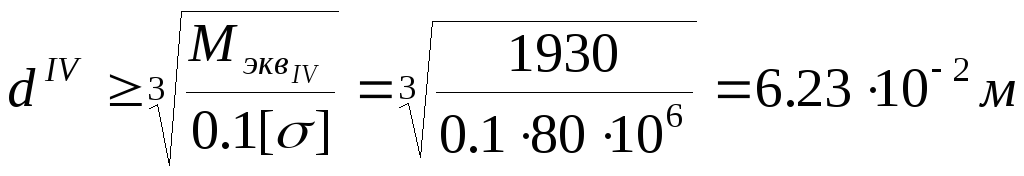 ,
,![]() =62.3
мм.
=62.3
мм.4.3 Расчет брусьев прямоугольного сечения
![]() и
и![]() ,
а также крутящий момент
,
а также крутящий момент![]() (рис. 4.3).
(рис. 4.3).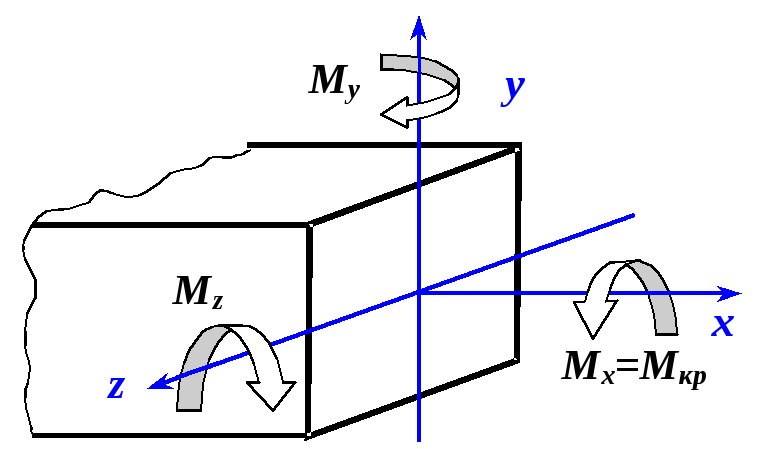

![]() ,
в которой
,
в которой![]() от
от![]() и
и![]() от
от![]() положительны, или точка
положительны, или точка![]() ,
в которой
,
в которой![]() от
от![]() и
и![]() от
от![]() также одного знака, но отрицательны.
Касательные напряжения от крутящего
момента в этих точках равны нулю. Таким
образом, в этих точках имеет место
линейное напряженное состояние.
также одного знака, но отрицательны.
Касательные напряжения от крутящего
момента в этих точках равны нулю. Таким
образом, в этих точках имеет место
линейное напряженное состояние.![]() (или
(или![]() ),
лежащая в середине длинной стороны
прямоугольника. Кроме того, в этой точке
действуют максимальные нормальные
напряжения от изгибающего момента
),
лежащая в середине длинной стороны
прямоугольника. Кроме того, в этой точке
действуют максимальные нормальные
напряжения от изгибающего момента![]() .
.![]() (или
(или![]() ),
расположенной в середине короткой
стороны также действуют касательные
напряжения (несколько меньшие
),
расположенной в середине короткой
стороны также действуют касательные
напряжения (несколько меньшие![]() )
и максимальные нормальные напряжения
от
)
и максимальные нормальные напряжения
от![]() .
.![]() ,
,![]() (
(![]() ,
,![]() )
имеет место плоское напряженное
состояние, которое обуславливает
использование гипотез прочности при
расчетах на прочность. Для пластичных
материалов применяютIII
(наибольших касательных напряжений) и
IV
(энергетическую) гипотезы прочности.
)
имеет место плоское напряженное
состояние, которое обуславливает
использование гипотез прочности при
расчетах на прочность. Для пластичных
материалов применяютIII
(наибольших касательных напряжений) и
IV
(энергетическую) гипотезы прочности.![]() :
:![]() ;
;![]() .
.![]() :
:![]() ;
;![]() ,
,![]() .
.![]() :
:![]() ;
;![]() ,
,![]() .
.![]() .
.![]() . (4.7)
. (4.7)![]() =0.9
кН на свободном конце. Определить в
точках
=0.9
кН на свободном конце. Определить в
точках![]() и
и![]() защемленного сечения расчетные
напряжения по третьей теории прочности
(рис. 4.5).
защемленного сечения расчетные
напряжения по третьей теории прочности
(рис. 4.5).
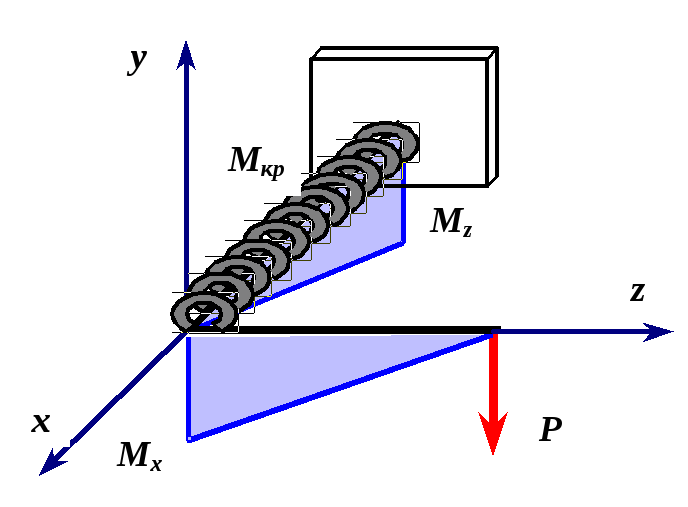
![]() в защемленном сечении будут действовать
изгибающий и крутящий моменты.
в защемленном сечении будут действовать
изгибающий и крутящий моменты.![]()
![]() .
.![]() :
:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.![]()
![]() :
:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.![]() .
.5. Общий случай сложного сопротивления
![]() и
и![]() ,
прямоугольное сечение в пределах
элемента длиной
,
прямоугольное сечение в пределах
элемента длиной![]() ,
требуется выполнить следующие расчеты:
,
требуется выполнить следующие расчеты:
![]() и
и![]() ,
исходя из заданных размеров прямоугольного
сечения элемента бруса длиной
,
исходя из заданных размеров прямоугольного
сечения элемента бруса длиной![]() ,
,![]() и
и![]() .
.![]() считать ориентированным так, что
плоскость наибольшей жесткости совпадает
с плоскостью действия максимального
изгибающего момента.
считать ориентированным так, что
плоскость наибольшей жесткости совпадает
с плоскостью действия максимального
изгибающего момента.
![]() ,
м
,
м
![]() ,
м
,
м
![]() ,
м
,
м
![]()
![]() ,
см
,
см
![]()
![]() ,
МПа
,
МПа
![]() ,
изгибающих
,
изгибающих![]() и крутящих
и крутящих![]() моментов . Поперечными силами
моментов . Поперечными силами![]() в расчетах, как правило, пренебрегают,
так как их влияние незначительно. Для
ломаного бруса, показанного на рис.
5.1, эпюры внутренних силовых факторов
приведены на рис. 5.2.
в расчетах, как правило, пренебрегают,
так как их влияние незначительно. Для
ломаного бруса, показанного на рис.
5.1, эпюры внутренних силовых факторов
приведены на рис. 5.2.
![]() и
и![]() .
.![]() .
.![]() ,
изгибающий момент
,
изгибающий момент![]() ,
постоянный по длине участка, крутящий
момент
,
постоянный по длине участка, крутящий
момент![]() ,
а также продольная сжимающая сила
,
а также продольная сжимающая сила![]() .
.![]() ориентируем так, чтобы плоскость
наибольшей жесткости совпадала с
плоскостью действия максимального
изгибающего момента
ориентируем так, чтобы плоскость
наибольшей жесткости совпадала с
плоскостью действия максимального
изгибающего момента![]() .
Положение плоскости наибольшей жесткости
определяется жесткостью поперечного
сечения относительно главных центральных
осей
.
Положение плоскости наибольшей жесткости
определяется жесткостью поперечного
сечения относительно главных центральных
осей![]() и
и![]() ,
в частности, величиной максимального
момента сопротивления. В данном случае
(рис. 5.3)
,
в частности, величиной максимального
момента сопротивления. В данном случае
(рис. 5.3)![]() ,
,
![]() ,
,![]() ,
т.к.
,
т.к.![]() .
.![]() (
(![]() ).
Следовательно, сечение должно быть
расположено так, как показано на рис.
5.3.
).
Следовательно, сечение должно быть
расположено так, как показано на рис.
5.3.![]() )
и касательных (от
)
и касательных (от![]() )
напряжений (рис. 5.3).
)
напряжений (рис. 5.3).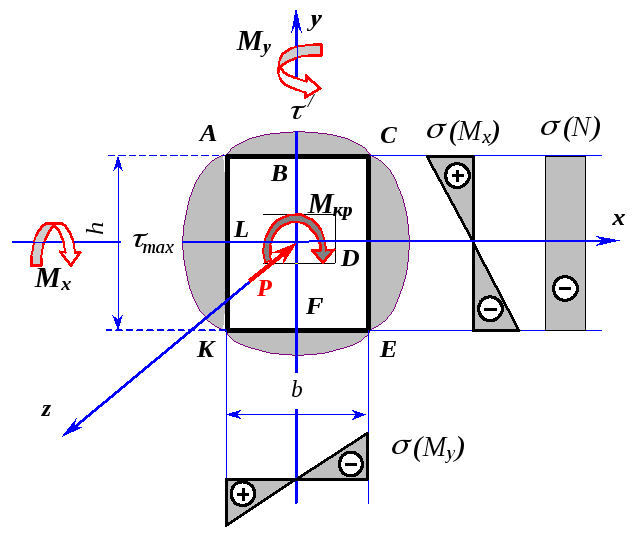
![]() ,
где суммируются нормальные напряжения
от
,
где суммируются нормальные напряжения
от![]() ,
касательные напряжения равны нулю,
,
касательные напряжения равны нулю,![]() ,
где суммируются нормальные напряжения
от
,
где суммируются нормальные напряжения
от![]() ,
а касательные напряжения от
,
а касательные напряжения от![]() принимают максимальные значения,
принимают максимальные значения,![]() ,
где суммируются нормальные напряжения
от
,
где суммируются нормальные напряжения
от![]() ,
а касательные напряжения равны
,
а касательные напряжения равны![]() .
.![]() через величину
через величину![]() .
Так как по условию задачи
.
Так как по условию задачи![]() =1.3,
то получаем
=1.3,
то получаем![]() .
.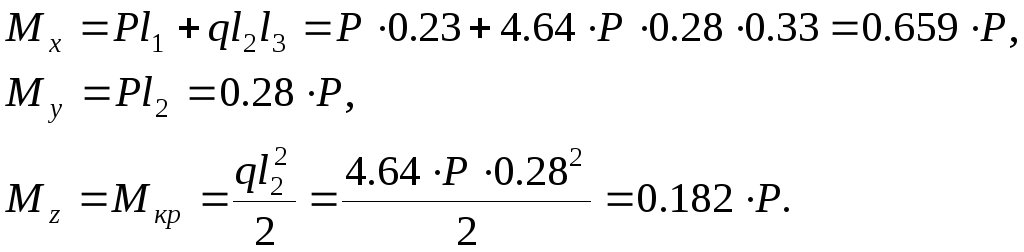
![]() и
и![]() см моменты сопротивления принимают
следующие значения:
см моменты сопротивления принимают
следующие значения: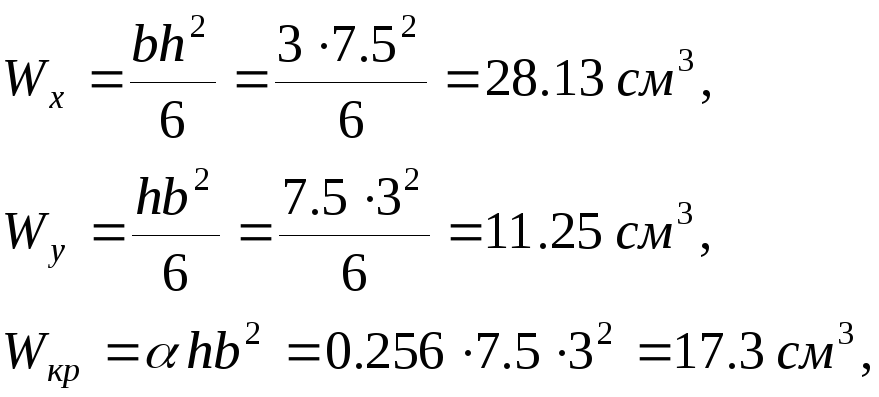
![]() .
.![]() .
В точке
.
В точке![]() имеют место только нормальные напряжения,
поэтому на основании принципа
независимости действия сил
имеют место только нормальные напряжения,
поэтому на основании принципа
независимости действия сил![]()
![]() ,
,![]() .
.![]() .
Для точки
.
Для точки![]() имеем
имеем![]()
![]() ,
,![]() .
.![]() имеют место нормальные и касательные
напряжения, используем условие прочности
по третьей гипотезе
имеют место нормальные и касательные
напряжения, используем условие прочности
по третьей гипотезе![]() .
.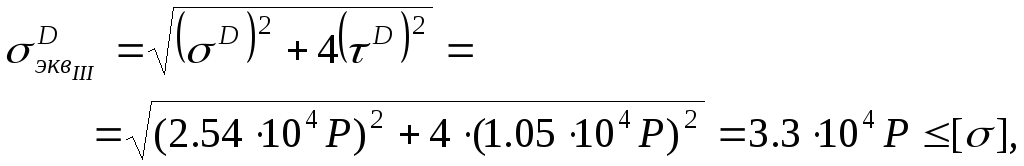
![]() .
.![]() .
Для точки
.
Для точки![]() имеем
имеем![]()
![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() .
.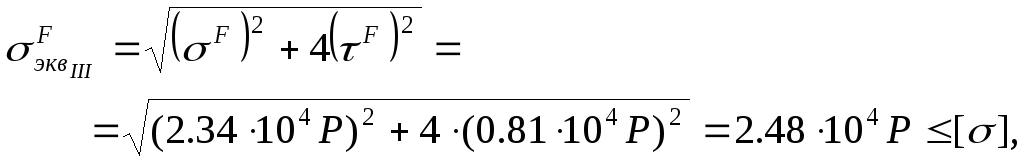
![]() .
.![]() должна быть меньше или равна 3.3 кН, т.е.
точка
должна быть меньше или равна 3.3 кН, т.е.
точка![]() оказалась самой опасной из трех.
оказалась самой опасной из трех.3. Определение диаметров круглых сечений элементов ломаного бруса при ,.
![]() .
.![]() .
Условие прочности будет иметь вид
.
Условие прочности будет иметь вид![]() .
.![]() .
.![]() .
.![]() .
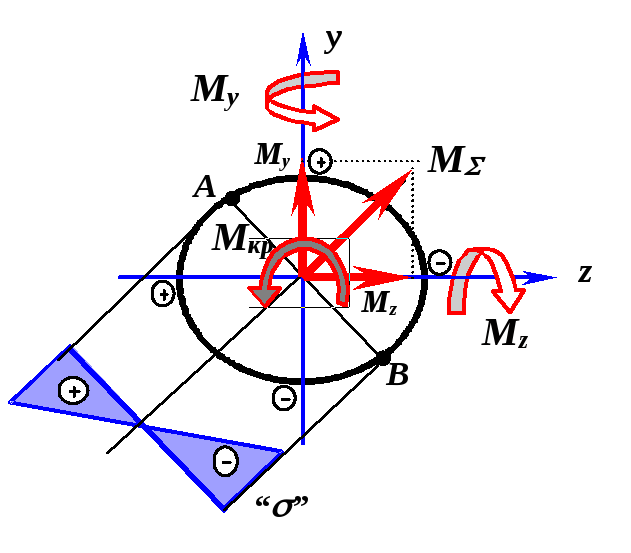
.![]() и
и![]() принимают
максимальные значения, а крутящий
момент
принимают
максимальные значения, а крутящий
момент![]() ,
т.е. имеет место изгиб с кручением бруса
круглого поперечного сечения (см. раздел
4.1). На рис. 5.4 два изгибающих момента
приведены к одному суммарному и показаны
опасные точки сечения
,
т.е. имеет место изгиб с кручением бруса
круглого поперечного сечения (см. раздел
4.1). На рис. 5.4 два изгибающих момента
приведены к одному суммарному и показаны
опасные точки сечения
![]() и
и
![]() .
.
![]() ,
,![]() ,
,![]() .
.![]() .
.![]() .
.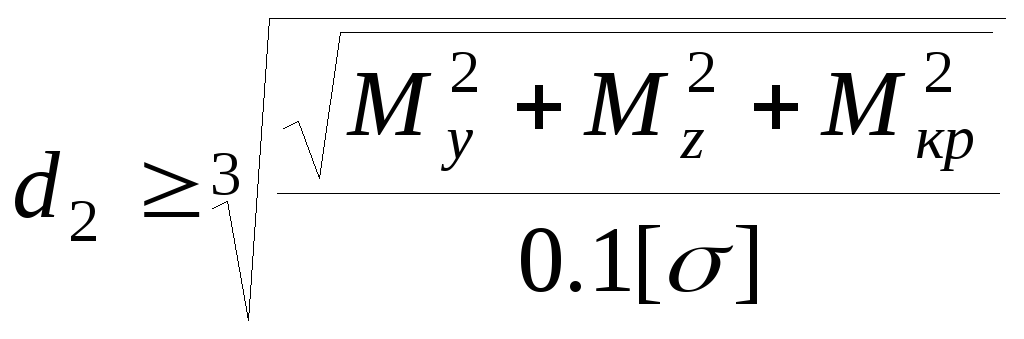 ,
,![]() .
.![]() .
.
3
42
4
41
5
40
6
39
7
38
8
37
9
36
10
35
11
34
12
33
13
32
14
31
15
30
16
29
17
28
18
27
19
26
20
25
21
24
22
23
