План прискорень

Плани прискорень будують аналогічно планам швидкостей.

Планом прискорень будь-якого твердого тіла (ланки) назива­ють геометричне місце кінців векторів прискорень крайніх його точок, відкладених з однієї довільної точки, що називається полю­сом плану прискорень.

Теорема подібності для планів прискорень формулюється так.

План прискорень будь-якого тіла (ланки) подібний до тіла і повернутий відносно нього на деякий невизначений кут.

Розглянемо методику побудови планів прискорень на прикладі кривошипно-повзункового механізму (див. рис. 4.2). Вихідними даними для побудови плану прискорень є положення ланок механізму (план механізму) і план швидко­стей. Рівняння, які використовуються при побудові плану прискорень, різняться тільки тим, що повні прискорення точки розкладають на певні складові. У даному випадку (рис. 4.3, а) повне прискорення точки А є геометричною сумою нормального (доцентрового) і дотичного (тангенціального) прискорень:

Нормальне прискорення напрямлене по лінії АО до центра обертання кривошипа О, дотичне – перпендику­лярно до АО і направлене в бік напрямку кутового прискорення ланки 1. Модулі цих прискорень находять із співвідношень

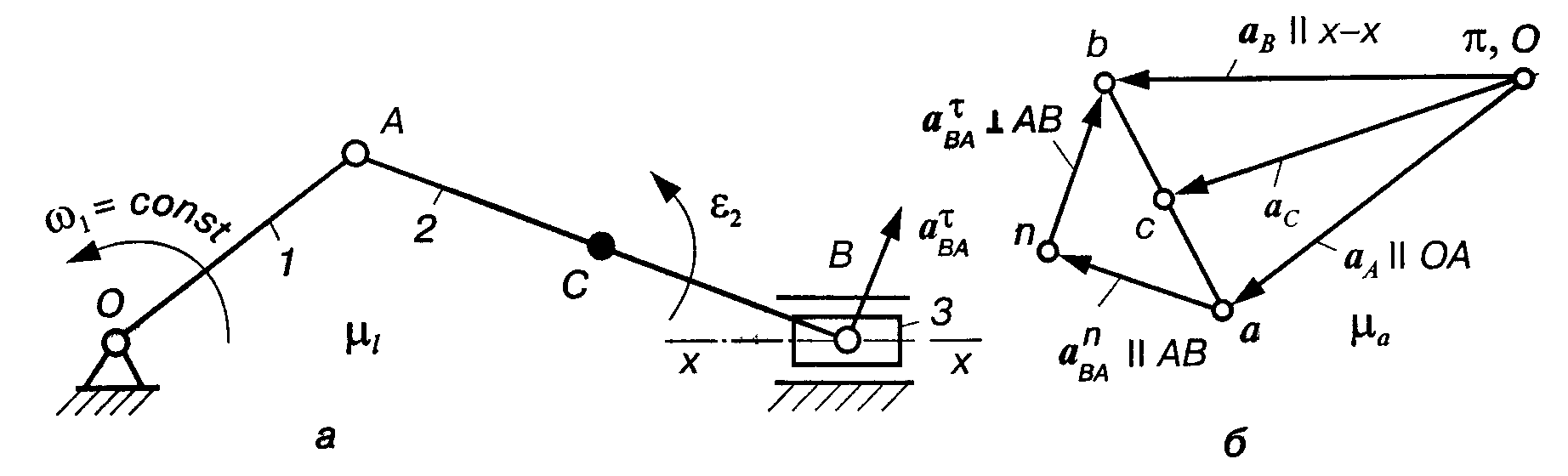
Рис. 4.3

Якщо початкова ланка обертається рівномірно (₁= соnst), то , а отже, у даному випадку тобто прискорення точки .

Прийнявши деяку точку ті за полюс плану прискорень (рис. 4.3,б), відкладемо вектор, який зображує нормальне приско­рення точки А, у вигляді відрізка а. Тоді масштаб (масштабний коефіцієнт) прискорень знайдемо зі співвідношення

Прискорення точки В знайдемо з рівняння, аналогічного рівнянню (4.3):

a_B = a_A+a_BA (4.4)

де вектор прискорення a_B направлений уздовж напрямної х—х. Розкладаємо відносне прискорення a_BA на дві складові:

Тоді рівняння (4.4) запишемо у вигляді

(4.5)

Вектор нормального прискорення направлений уздовж лінії ВА від точки В до А, а його модуль

На плані прискорень зображено відрізком ап= /_a, який прикладено своїм початком у точку а (згідно з правилом складання векторів). Через його кінець (точку п) проведено лінію дотичного прискорення з направленого перпендику­лярно до лінії АВ , потім через полюс  — напрямок прискорення точки В (|| х—х). Тоді точка перетину напрямків прискорень а_B i визначить точку b — кінець векторів а_B і . З'єднавши точки а і b, знайдемо вектор повного приско­рення і тим самим побудуємо план прискорень шатуна АВ.

Положення точки с на плані прискорень можна визначити ме­тодом подібності, склавши пропорцію ( ), з якої можна визначи­ти відрізок ас. Тоді прискорення точки С становить а_C = (с)_a.

Модуль кутового прискорення ланки 2 . Для ви­значення напрямку перенесемо вектор дотичного прискорення у точку В (рис. 3.11, а) і спостерігатимемо, в який бік цей век­тор буде обертати шатун АВ відносно вибраного полюса (точка А). У нашому випадку кутове прискорення направлене проти руху годинникової стрілки. Отже, рух шатуна АВ в цьому положенні сповільнений, оскільки кутова швидкість має інший напрямок (див. рис. 4.2,а).

Лекція 5

ПРИКЛАДИ ПОБУДОВИ ПЛАНІВ ШВИДКОСТЕЙ

І ПРИСКОРЕНЬ МЕХАНІЗМІВ II КЛАСУ

ПЛАНИ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ ШАРНІРНОГО

ЧОТИРИЛАНКОВОГО МЕХАНІЗМУ

Як і для кривошипно-повзункового механізму, повинні бути за­дані кінематична схема механізму (рис. 5.1,а) і закон руху по­чаткової ланки — кривошипа 1 (₁= соnst).

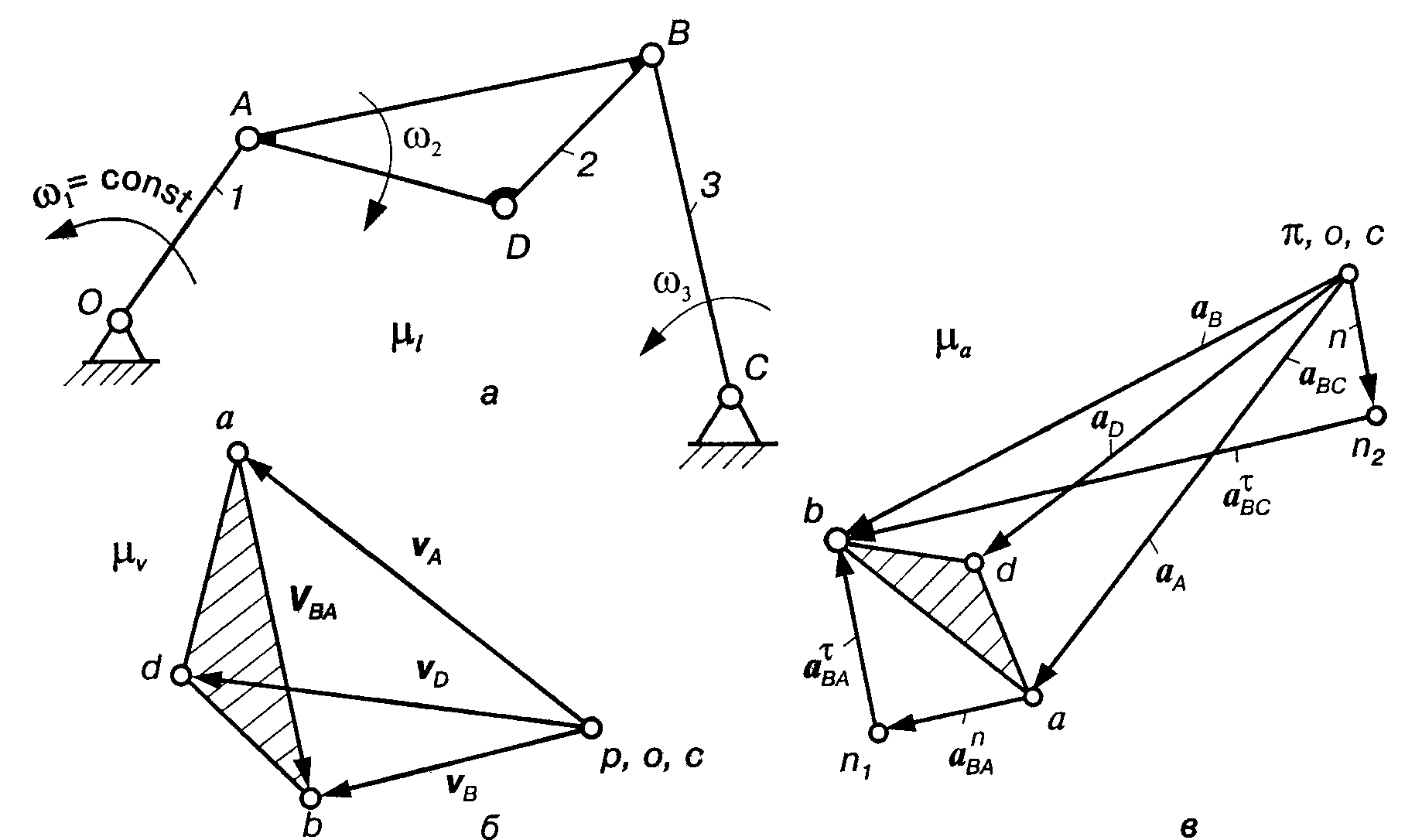
Рис. 5.1

Визначимо модуль швидкості точки А (V_A=₁l_OA) відкладемо вектор цієї швид­кості у масштабі _V(V_AOA), попередньо вибравши відрізок ра. Масштаб плану швидкостей одержимо за відомою формулою:

Для визначення швидкості точки В, яка одночасно належить ланкам 2 і 3, складемо векторні рівняння:

V_B = V_A+ V_BA; V_B = V_C +V_BC. (5.1)

За першим рівнянням (5.1) через кінець вектора V_A (точка а) , проведемо лінію відносної швидкості V_BA точки В відносно точки А (V_BAАВ), а через точку р — лінію відносної швидкості V_BC В відносно точки С (V_BCВC). Точка С як нерухома (V_BC = 0) по­трапляє у полюс плану швидкостей, там знаходиться і точка О (V_O=0). Точка перетину ліній-напрямків швидкостей V_BA і V_BC= V_B визначає точку b, а отже, і величину цих векторів у масштабі _V:

V_BA=(ab)_V, V_B=(pb)_V.

Швидкість точки D, що належить ланці 2, можна визначити за допомогою теореми подібності для плану швидкостей, згідно з якою можна записати такі пропорції:

(5.2)

З цих пропорцій знайдемо відрізки:

за допомогою яких побудуємо , подібний до . З'єднавши точку d з полюсом р, отримаємо швидкість точки D:V_D=(pd)_V. Її можна визначити також методом векторних рівнянь, розглянувши швидкість точки D через швидкості точок А і В, тобто записавши рівняння

V_D= V_A+ V_DA; V_D= V_B+ V_DB,

де V_DA  DA; V_DB  DB.

Кутові швидкості ланок 2 і 3 знайдемо, використавши відносні швидкості V_BA i V_BC:

₂= V_BA/l_AB; ₃= V_BC/l_BC= V_B/l_BC.

Щоб встановити напрямок кутової швидкості 2, перенесемо вектор V_BA y точку В і розглянемо рух ланки 2 відносно точки А; для кутової швидкості ₃ перенесемо вектор V_BC також у точку В і розглянемо рух ланки 3 відносно точки С. У даному випадку ₂ напрямлена за рухом годинникової стрілки, ₃ — проти руху годинникової стрілки.

Побудову плану прискорень цього механізму також розпоч­немо з ланки 1. Прискорення точки А при ₁ = const визначимо за формулою нормального прискорення .

Вибравши полюс плану прискорень  (рис. 5.1,в), відкладемо від нього відрізок па, який відповідає прискоренню точки А у масштабі _a . Прискорення точки А спрямоване по лінії АО від точки А до точки О.

Для знаходження прискорення точки В складемо два век­торні рівняння:

(5.3)

Згідно з першим рівнянням системи (5.3) кінець першого век­тора а_A повинен збігатися з початком вектора нормального прискорення точки В відносно А, величина якого визначається за формулою , або .

У вибраному масштабі цей вектор буде зображено відрізком , мм. Прискорення направлене вздовж осі ланки АВ від точки В до точки А. Через точку п₁ згідно з цим самим рівнянням необхідно провести лінію-напрямок дотичного прискорення , величина останнього невідома, відомий лише його напрямок — перпендикулярний до лінії АВ.

Розглянемо друге рівняння (5.3). Прискорення точки С дорівнює нулю, тому точка с збігається з полюсом плану. При­скорення направлене від точки В до точки С. Відрізок , який відповідає прискоренню , на плані відкладаємо від точки . Через точку n₂ проведемо лінію-напрямок дотичного прискорення до перетину з лінією-напрямком прискорення . Точка перетину b цих ліній визначить величину і напрямок прискорення точки В та величини дотичних прискорень (у масштабі _a).

Прискорення точки D отримаємо методом подібності, побу­дувавши подібний до ланки АBD трикутник аbd. Відрізки аd і bd визначимо із пропорцій (5.2). Щоб знайти прискорення точки D, можна також записати векторні рівняння, виразивши при­скорення точки D через прискорення точок А і В, тобто

(5.4)

Плани прискорень на основі рівнянь (5.4) будуються так само, як і для точки В (5.3).

Модуль кутових прискорень ланок 2 і 3 знайдемо за формулами

Для визначення напрямку і перенесемо вектори і y точку В і розглянемо, в який бік ці вектори повер­тають ланки відповідно АВ і ВС.