Группировка рабочих по выработке продукции
Группы рабочих по выработке продукции, кг/чел., |
Середина
интервала,
|
Количество
рабочих, чел.,
|
2-4 |
3 |
2 |
4-6 |
5 |
7 |
6-8 |
7 |
8 |
8-10 |
9 |
3 |
Определите абсолютные и относительные показатели вариации выработки продукции рабочими.
Решение:
Поскольку в условии группировка рабочих представлена в виде интервального вариационного ряда, предварительно надо определить середины интервалов ( ) как полусуммы их границ. Середины интервалов соответственно группам составят (кг/чел.): 3; 5; 7 и 9.
Размах вариации составит:
Среднюю выработку по сгруппированным данным определяем по формуле средней арифметической взвешенной:
;
Среднее линейное отклонение:
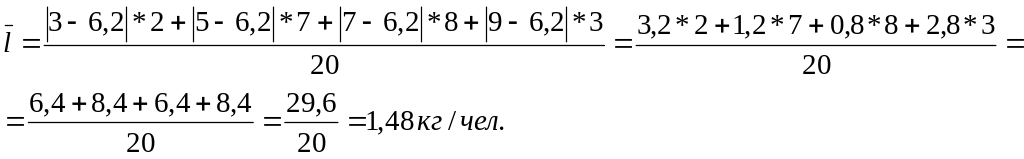
Дисперсия выработки рабочих составит:
Среднее квадратическое отклонение равно:
4. Свойства дисперсии
Дисперсия имеет ряд математических свойств, которые могут быть использованы для упрощения ее расчета.
1. Если индивидуальные значения признака уменьшить или увеличить на некоторое постоянное число, то дисперсия не изменится.
;
.
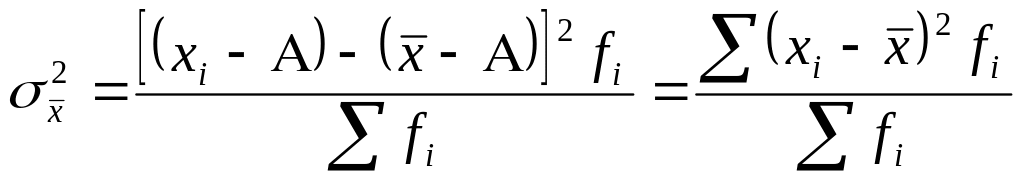(7.14)
2. Если индивидуальные значения признака разделить или умножить на некоторое постоянное число, то дисперсия соответственно уменьшится (увеличится) в квадрат от постоянного числа раз:
;
.
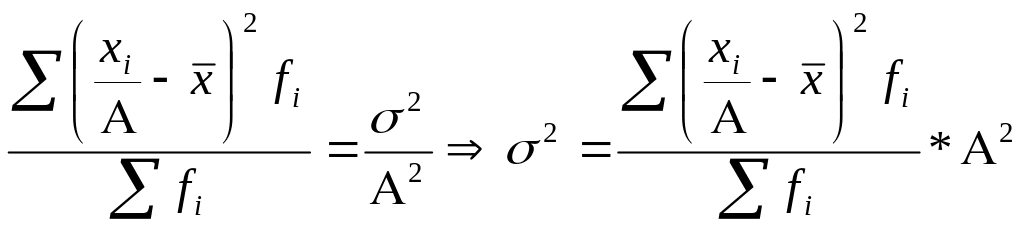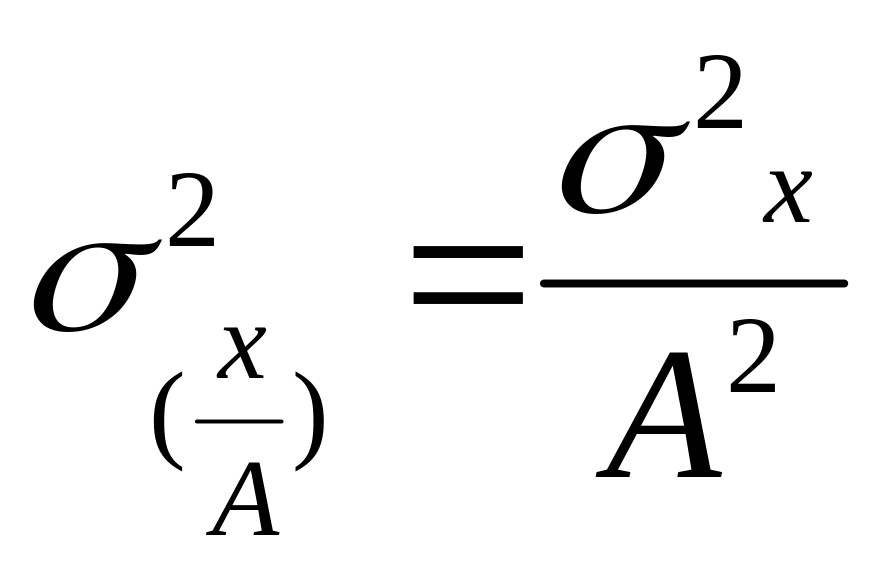(7.15)
3. Дисперсия, рассчитанная от постоянной величины, больше дисперсии, рассчитанной от средней, на квадрат разности между средней величиной и постоянной:
;
.
(7.16)
4. Если постоянную величину приравнять к нулю, то дисперсия будет равна разности между средним квадратом значений признака и квадратом средней:
(7.17)
или
.
(7.18)
При
получим:
.
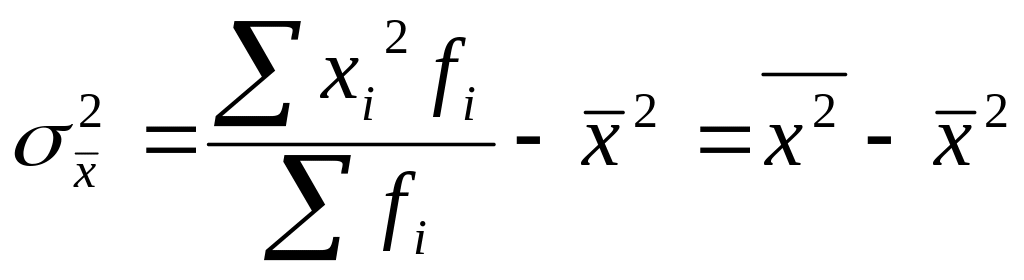(7.19)
5. Дисперсия альтернативного признака
Наряду с вариацией количественных признаков, часто необходимо определить вариацию качественных или альтернативных признаков.
Альтернативным называется признак, который может принимать только два значения: наступление или ненаступление события. На практике, например, изучается качество изготовленной продукции с помощью разделения ее на стандартную и бракованную. Условно считается, что альтернативный признак принимает значение, равное 1, если событие наступило, т.е. обследуемая единица обладает данным признаком, и равное 0, если событие не наступило.
Удельный вес (доля)
значений признака, для которых событие
наступило, обозначим через, а для которых
не наступило – через
:
.
(7.20)
Дисперсия альтернативного признака определяется по формуле:
.
(7.21)
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц не обладающих данным признаком. Тогда среднее квадратическое отклонение альтернативного признака равно:
.
(7.22)
В случае, когда
значения
и
неизвестны, для расчета дисперсии они
принимаются:
;
.
Тогда дисперсия будет равна:
.
Дисперсия альтернативного признака используется в выборочном наблюдении.
Пример 3. При приеме партии молока, фасованного в полимерные пакеты, в партии из 1000 пакетов двадцать имели дефекты упаковки. Определите дисперсию и среднее квадратическое отклонение доброкачественных пакетов молока.
Решение:
Доля доброкачественных пакетов:
.
Доля дефектных пакетов:
.
Тогда:
.
.