Нереализуемые оптимальные решения

Рассмотрим некоторые причины, которые обуславливают невозможность принятия и реализации оптимальных решений.

Физическая нереализуемость. Оптимальное решение может относиться к категории нереализуемых решений. Причина возникновения подобной ситуации определяется недостаточно полным учетом ограничений ресурсов в математической модели. Так, например, решение статической задачи может не учитывать ограничения по имеющимся трудовым ресурсам в смысле их квалификации. В динамических задачах известны случаи, когда для расчета оптимального решения необходимо предварительно иметь бесконечную реализацию исходного процесса. Существование физически нереализуемых решений представляет определенный практический интерес как средство оценки потенциально достижимой эффекта (предельное значение критерия).

Техническая нереализуемость. Реализация или даже расчет оптимального решения могут оказаться невозможными чисто по техническим причинам, определяемыми текущим состоянием имеющихся в распоряжении разработчика технических средств. Такая ситуация возникает в том случае, когда объем реальной задачи не соответствует техническим характеристикам вычислителя или вычислитель неисправен или отсутствует, или произошел сбой вычислений, утрата данных, использование ошибочных данных и т.п. К этой же категории следует отнести ситуации, когда полученные результаты решения уже не представляют интереса для исследователя, поскольку они поступают после принятия решения.

Как следствие, при возникновении нереализуемых оптимальных решений приходится пользоваться методами разработки рациональных решений.

Разработка альтернатив для принятия рациональных решений

Отметим, что на практике подавляющее большинство решений, принимаемых к разработке и реализации, относится к категории рациональных. Если используются методы теории принятия решений, то качество разработки рациональных решений в первую очередь определяется качеством разработки альтернатив.

Разработка рациональных решений также начинается с формулирования проблемы и определения цели или целей ее разрешения, на основе которой формулируется критерий или критерии и принцип компромисса. Кроме этого, определяются ограничения, который могут существенно сократить число разрабатываемых альтернатив.

Разработка альтернатив может проводиться автоматическими, автоматизированными или ручными методами. Автоматические методы предусматривают использование оптимальных методов решения задачи в случае, когда имеет место их физическая или техническая нереализуемость. Так, например, может быть автоматически сгенерировано ограниченное число вариантов решения или варианты, дающие приближенное решение. Другим вариантом использования автоматических методов может быть генерация случайного набора альтернатив, например, на основе использования датчиков случайных чисел.

Автоматизированные методы подразумевают участие в процедуре генерации альтернатив человека. Им может быть, например, эксперт или сам постановщик задачи. В этом случае можно существенно сократить количество альтернатив за счет отбраковки «заведомо плохих».

Наконец, ручные методы не предусматривают существенной автоматизации и используются в тех случаях, когда альтернативы оказываются, например, весьма сложными или не поддающимися формализации.

При использовании автоматизированного и ручного метода генерации альтернатив целесообразно первоначально попытаться определить множество допустимых значений альтернатив. Очевидно, что это множество обязательно должно удовлетворять ограничениям задачи. Тем не менее, в некоторых случаях на этапе разработки альтернатив, особенно если их очень много, можно вводить дополнительные ограничения, отбрасывающие заведомо худшие.

Найденные альтернативы должны быть подвергнуты сравнению с критерием и в качестве рационального решения должна выбираться альтернатива с наилучшим значением критериальной функции. Методы разработки альтернатив рациональных решений представлены на рис. 29.

Имеющиеся в распоряжении исследователя альтернативы не обязательно исчерпывают весь возможный список, поскольку некоторые из них могут быть еще не найдены (например, не придуман ход в шахматной партии) или они еще в принципе не существуют, но могут появиться в будущем или были когда–то в прошлом (например, вариант обмена квартиры). Оптимальные решения в таких случаях просто не существуют, поскольку никто не может гарантировать, что не будет придуман ход лучше или не появится новый вариант обмена.

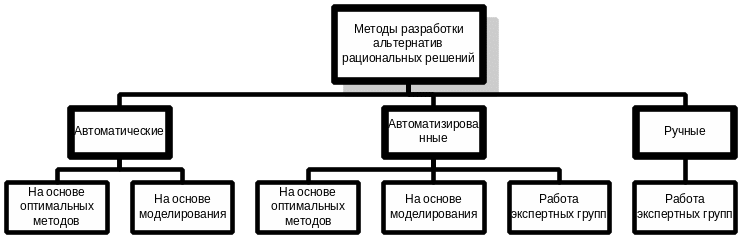
Рис. 29. Методы разработки альтернатив при принятии рациональных решений

Особый интерес представляет случай, когда ищется только две альтернативы решения. Подобного рода решения называют бинарными [25] или решениями типа делать – не делать [29]. Заметим, что решение подобного рода в свое время принимал Гамлет.

Бинарные решения встречаются в практической деятельности достаточно часто по той простой причине, что третья и последующие альтернативы могут просто не отыскиваться. Действительно, если решается вопрос «быть или не быть», то вопрос «как быть» неизбежно отходит на второй план. Процедура принятия бинарных решений ничем существенным не отличается от обычной и также заключается в сравнении альтернатив по критерию.

Если альтернативы найдены, то их выбор и, соответственно, принятие решения в рациональных задачах также осуществляется вручную. Все это в конечном итоге может привести к существенным затратам труда и времени.

В остальном процедура принятия решения ничем существенным не отличается от рассмотренной ранее при использовании оптимальных методов. Если критериев несколько, то используются методы решения многокритериальных задач. Наличие случайных параметров в альтернативах может переводить рассматриваемые задачи к задачам в условия риска и неопределенности. Методы решения подобных задач сводятся к расчету функции распределения критериального параметра и определению наиболее выгодной стратегии. Если критерий является неметрическим, то выбор альтернативы осуществляется за счет формулирования бинарных отношений (лучше – хуже). Во многих случаях оказываются применимы процедуры экспертного оценивания. Наконец известны варианты, когда подобные решения принимаются случайным методом, например, подбрасывая монетку.

Наличие большего числа альтернатив по сравнению со случаем бинарного решения технически усложняет процедуру их отбора, но не вносит в нее принципиальных изменений. Так, в отличие от бинарного случая, увеличивается количество сравнений альтернатив. Если выполняется, например, процедура их попарного сравнения, то общее число сравнений определяется как число сочетаний из количества альтернатив по два и может очень быстро расти, что может привести к технической нереализуемости решения. Искусство принятия решения заключается, в частности, в точном определении числа рассматриваемых альтернатив рационального решения, сохраняющих его в категории реализуемых и обеспечивающего наилучшие из числа возможных результаты.