
- •Медведева н.С., Моисеева ю.А., Степанов а.Г., Усикова и.В. Системы поддержки принятия решения Оптимальные методы и теория принятия решений
- •Содержание
- •2.5. Однокритериальная статическая задача в условиях неопределенности 60
- •2.6. Многокритериальные задачи 79
- •2.7. Динамические задачи разработки управленческого решения 86
- •2.8. Рациональные решения 101
- •2.9. Экспертные методы 107
- •Введение
- •1.Оптимальные методы
- •1.1.Методы поиска экстремумов функций
- •1.2.Учет ограничений на значения переменных
- •1.3.Использование Excel для поиска экстремумов функций
- •Лабораторная работа №1. Методы поиска экстремумов с помощью надстройки Поиск решения пакета Excel Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.Теория принятия решений
- •2.1.Основные понятия теории принятия решений
- •2.2.Математическая классификация задач разработки управленческого решения
- •2.3.Однокритериальная статическая задача разработки управленческого решения в условиях определенности
- •Лабораторная работа №2. Решение однокритериальной статической задачи в условиях определенности Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.4.Однокритериальная статическая задача разработки управленческого решения в условиях риска
- •Метод сведения задачи в условиях риска к детерминированной
- •Лабораторная работа №3. Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированной Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Методы оптимизации в среднем
- •Алгоритмический метод решения задачи в условиях риска
- •Лабораторная работа №4. Решение однокритериальной статической задачи в условиях риска алгоритмическим методом Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Метод Монте-Карло при решении задачи в условиях риска
- •Лабораторная работа №5. Решение однокритериальной статической задачи в условиях риска методом Монте-Карло Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Задачи в условиях риска с несколькими стохастическими параметрами
- •2.5.Однокритериальная статическая задача в условиях неопределенности
- •Игры с противником.
- •Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Игры с природой.
- •Лабораторная работа №7. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Игры с природой с экспериментами.
- •Лабораторная работа №8. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.6.Многокритериальные задачи
- •Лабораторная работа №9. Решение многокритериальной задачи Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.7.Динамические задачи разработки управленческого решения Общая постановка динамической задачи разработки управленческого решения
- •Метод сетевого планирования
- •Методы теории массового обслуживания
- •Метод динамического программирования
- •Задача управления запасами
- •Методы вариационного исчисления и теории оптимального управления
- •Метод сведения дискретной динамической задачи к статической
- •Лабораторная работа №10. Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.8.Рациональные решения Общий алгоритм разработки управленческого решения
- •Нереализуемые оптимальные решения
- •Разработка альтернатив для принятия рациональных решений
- •2.9.Экспертные методы Определение круга экспертов
- •Задачи, решаемые при проведении экспертизы
- •Разработка анкеты
- •Разработка методов обработки результатов
- •Проведение анкетирования, обработка и выдача результатов и принятие решения
- •Литература
- •Приложение а. Пример титульного листа отчета о выполнении лабораторной работы3.
- •Приложение б. Содержание отчетов о выполнении лабораторных работ Пример содержания отчета по лабораторной работе №2 «Решение однокритериальной статической задачи в условиях определенности»
- •Пример содержания отчета по лабораторной работе №3 «Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированной»
- •Пример содержания отчета по лабораторной работе №4 «Решение однокритериальной статической задачи в условиях риска алгоритмическим методом»
- •Пример содержания отчета по лабораторной работе №5 «Решение однокритериальной статической задачи в условиях риска методом Монте-Карло»
- •Пример содержания отчета по лабораторной работе №6 «Решение однокритериальной статической задачи в условиях неопределенности при играх с противником»
- •Пример содержания отчета по лабораторной работе №7 «Решение однокритериальной статической задачи в условиях неопределенности при играх с природой»
- •Пример содержания отчета по лабораторной работе №8 «Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами»
- •Пример содержания отчета по лабораторной работе №9 «Решение многокритериальной задачи»
- •Пример содержания отчета по лабораторной работе №10 «Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической»
- •Предметный указатель
Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником Задание
Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может быть в условиях неопределенности в результате возможных действий противника. Рассматривайте случай дуальной игры с противником с нулевой суммой и решите задачу.
Порядок выполнения работы
Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр.
На основе анализа ситуации в зависимости от возможных действий противника задайтесь возможными значениями случайного параметра
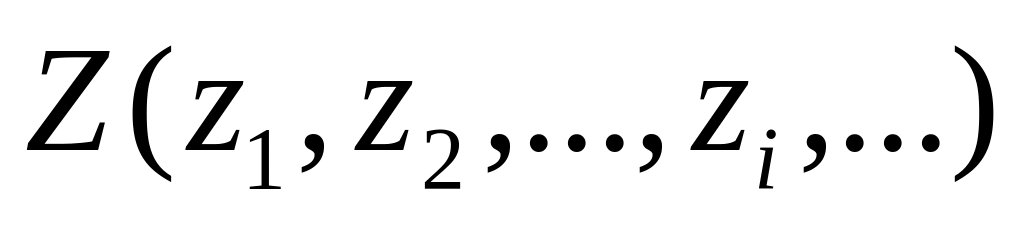 ,
для которых будет делаться расчет.
Каждое значение этого параметра будет
определять одну из наших стратегий и
одну из возможных стратегий противника.
,
для которых будет делаться расчет.
Каждое значение этого параметра будет
определять одну из наших стратегий и
одну из возможных стратегий противника.Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия противника угадана, то есть мы предполагаем значение параметра
 ,
и в результате действий противника он
принимает именно такое значение.
,
и в результате действий противника он
принимает именно такое значение.Постройте платежную матрицу, заполните ее диагональ значениями
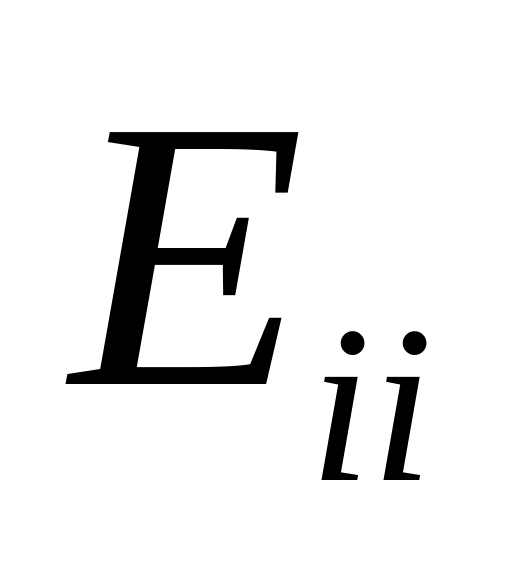 и отдельно запишите соответствующие
им решения
и отдельно запишите соответствующие
им решения
 .
.Используя выражение для показателя эффективности, рассчитайте значения критериальной функции
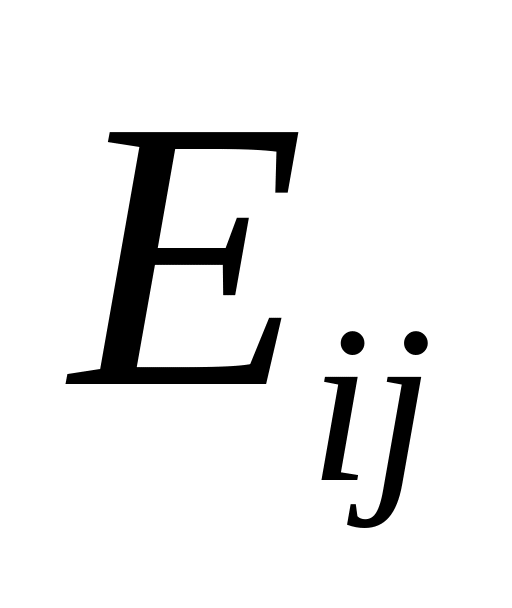 в предположении, мы используем стратегию
,
то есть решение
,
а в результате действий противника
параметр принимает значение
в предположении, мы используем стратегию
,
то есть решение
,
а в результате действий противника
параметр принимает значение
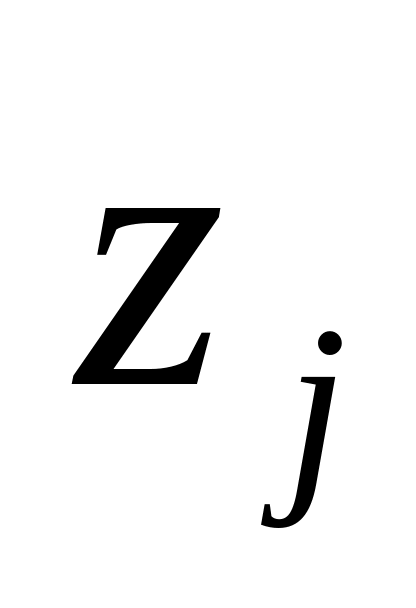 .
.Заполните значениями свободные клетки платежной матрицы.
Просматривая колонки платежной матрицы (
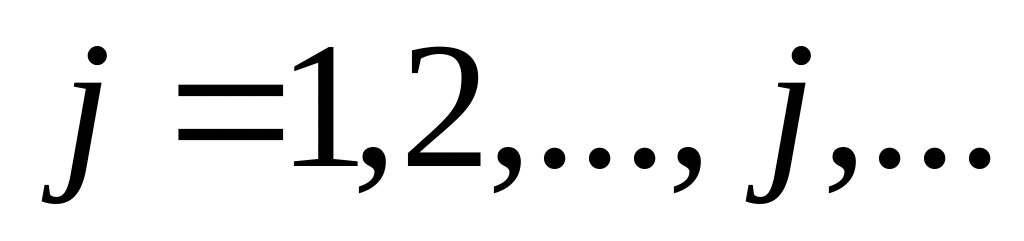 ),
найдите для каждой строки
наш гарантированный минимальный выигрыш
),
найдите для каждой строки
наш гарантированный минимальный выигрыш
 .
.Найдите номер нашей стратегии, обеспечивающей нам максимум гарантированного выигрыша (нижнюю цену игры)
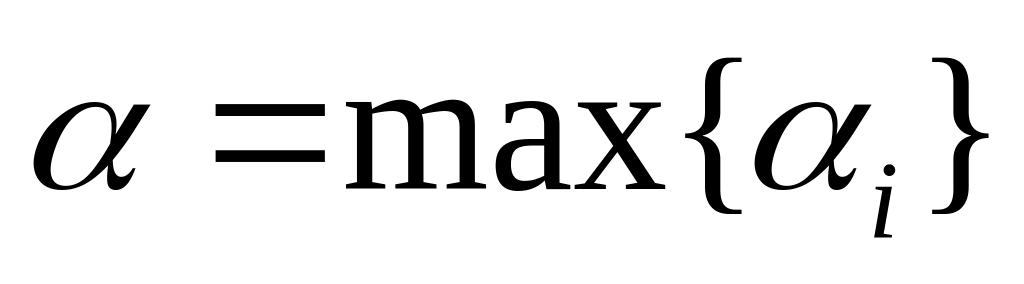 .
.Просматривая строки платежной матрицы (
 ),
найдите для каждого столбца
гарантированный максимальный проигрыш
противника (верхнюю цену игры)
),
найдите для каждого столбца
гарантированный максимальный проигрыш
противника (верхнюю цену игры)
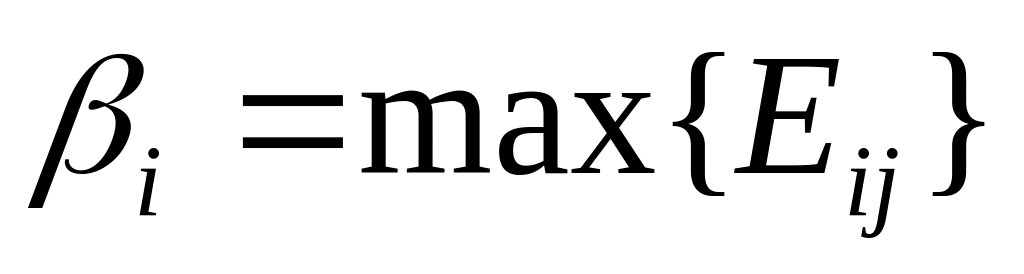 .
.Найдите номер стратегии противника, обеспечивающей ему минимум гарантированного выигрыша
 .
.Сравните верхнюю и нижнюю цены игры и определите факт наличия или отсутствия седловой точки.
Если седловая точка существует (
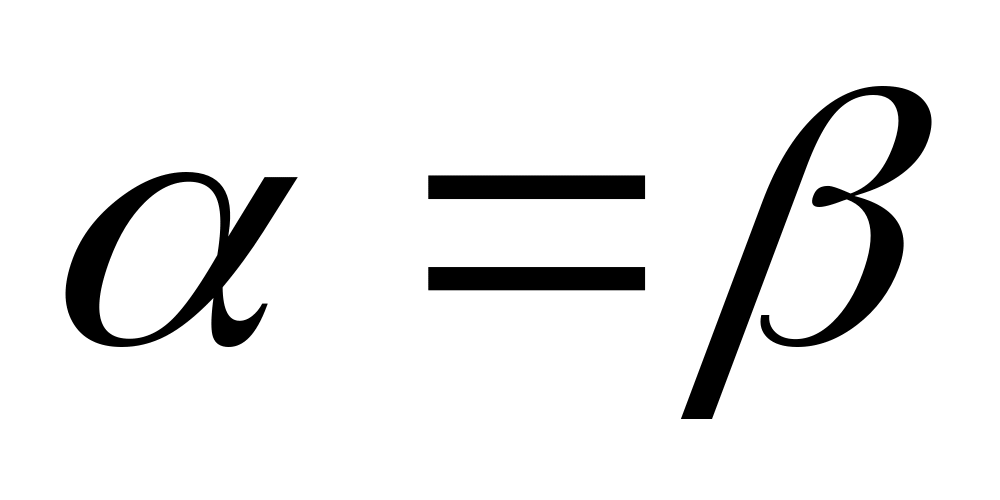 ),
то определите оптимальное решение
задачи
соответствующее номеру чистой стратегии,
обеспечивающей
.
),
то определите оптимальное решение
задачи
соответствующее номеру чистой стратегии,
обеспечивающей
.Если седловая точка отсутствует (
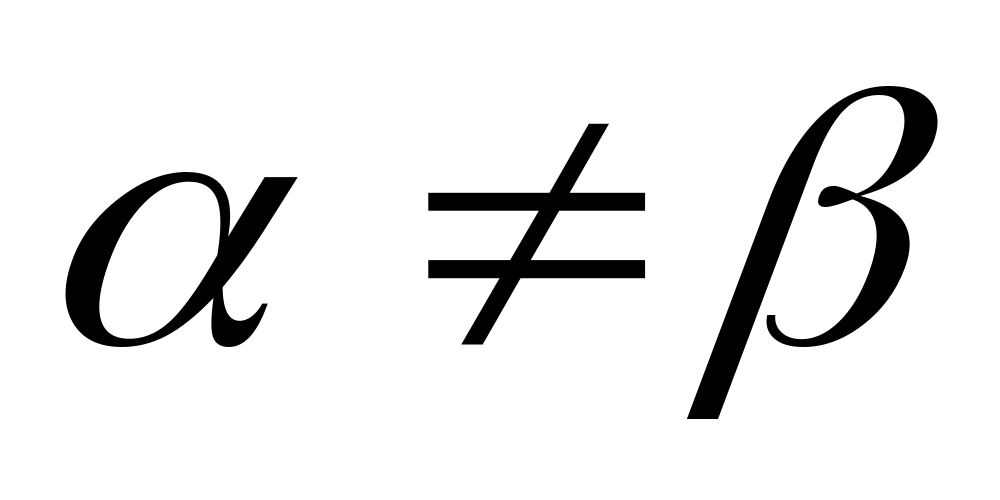 ),
то определите набор
своих стратегий
),
то определите набор
своих стратегий
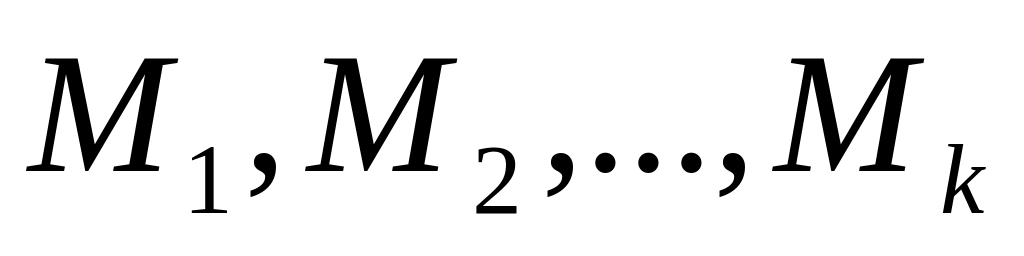 ,
которые обеспечивают значение
,
которые обеспечивают значение
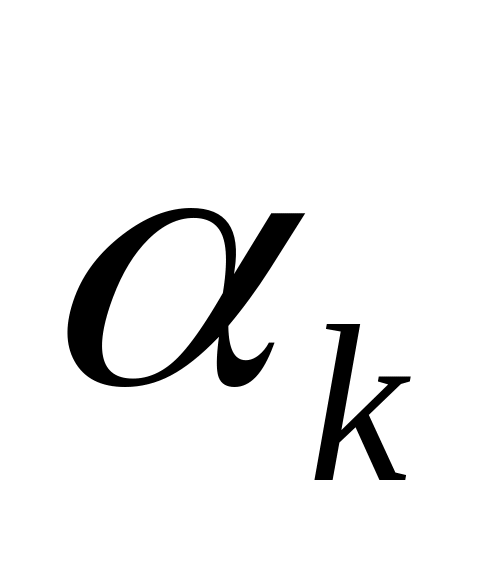 ,
имеют свой выигрыш
и будут чередоваться нами в случайном
порядке. Аналогично определите набор
,
имеют свой выигрыш
и будут чередоваться нами в случайном
порядке. Аналогично определите набор
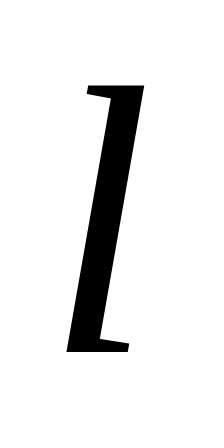 стратегий противника
стратегий противника
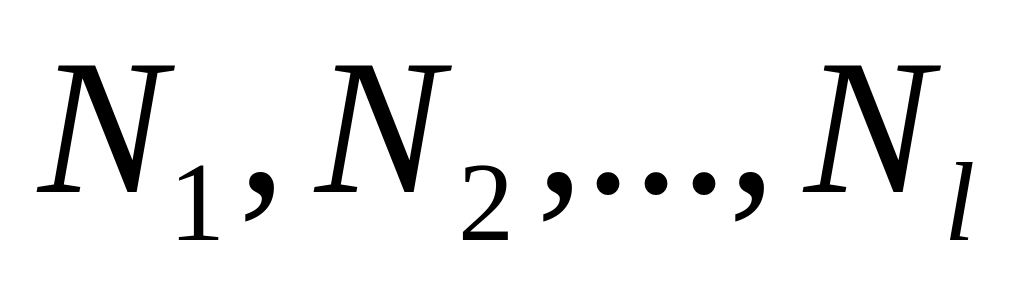 .
Сформируйте новую матрицу
.
Сформируйте новую матрицу
 размером
размером
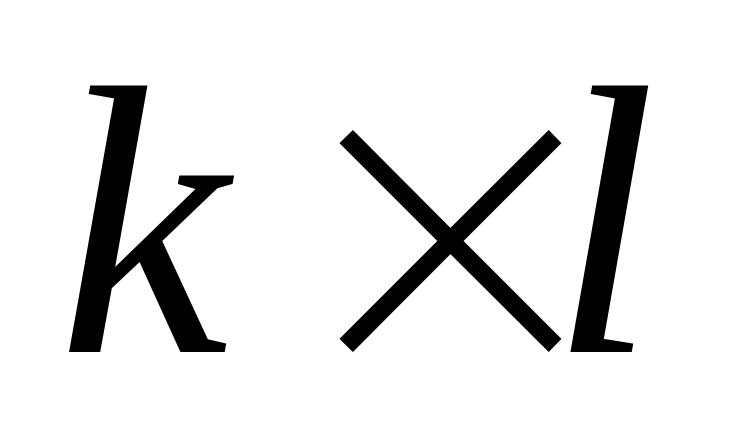 ,
элементы которой представляют выборку
из платежной матрицы в соответствии с
принятыми в рассмотрение стратегиями.
,
элементы которой представляют выборку
из платежной матрицы в соответствии с
принятыми в рассмотрение стратегиями.Отдельно сформулируйте и решите еще одну задачу линейного программирования, принимая во внимание ограничений
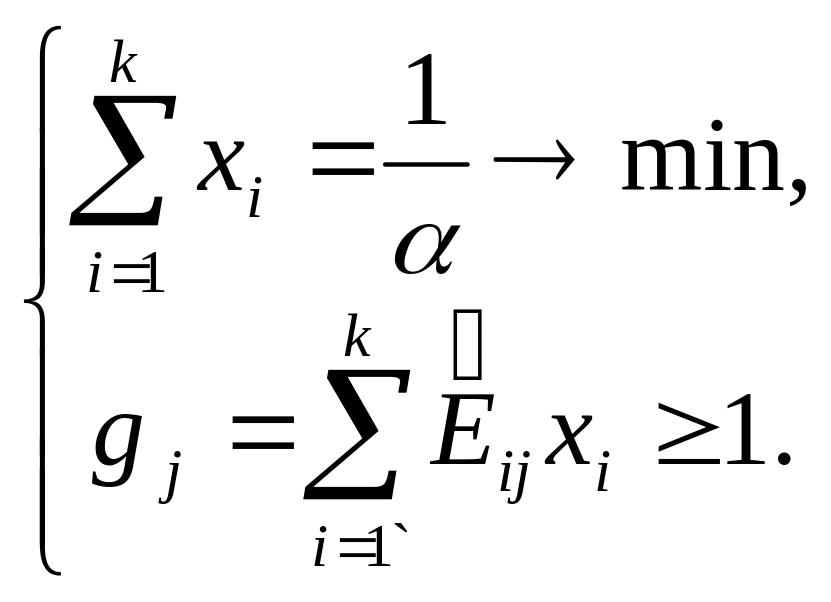
В соответствии с полученным решением
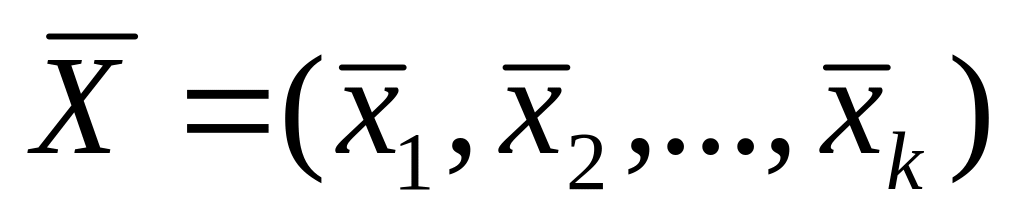 по формуле
по формуле
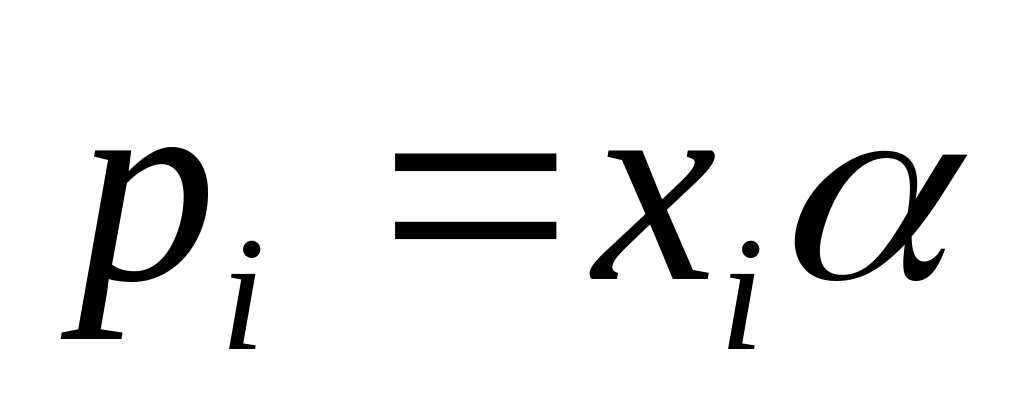 определите набор вероятностей
определите набор вероятностей
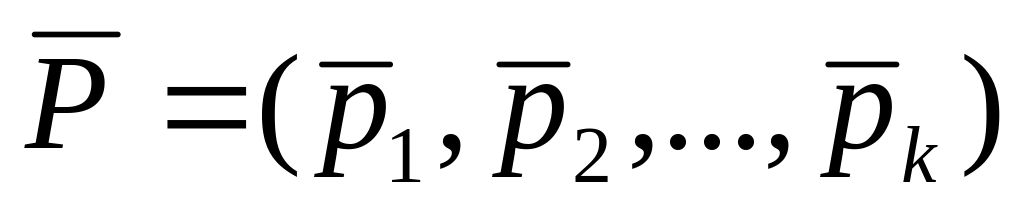 ,
с которыми необходимо чередовать
стратегии
.
,
с которыми необходимо чередовать
стратегии
.
Контрольные вопросы
Чем задача в условиях неопределенности отличается от задачи в условиях риска?
Что такое стратегия?
Что такое дуальная игра?
В каком случае игра может называться игрой с нулевой суммой?
В каком случае игра классифицируется как игра с противником?
Как составляется платежная матрица?
Чем элементы диагонали платежной матрицы отличаются от других элементов?
Что такое седловая точка?
В каком случае седловая точка может отсутствовать?
Что такое нижняя и верхняя цены игры?
