
- •Медведева н.С., Моисеева ю.А., Степанов а.Г., Усикова и.В. Системы поддержки принятия решения Оптимальные методы и теория принятия решений
- •Содержание
- •2.5. Однокритериальная статическая задача в условиях неопределенности 60
- •2.6. Многокритериальные задачи 79
- •2.7. Динамические задачи разработки управленческого решения 86
- •2.8. Рациональные решения 101
- •2.9. Экспертные методы 107
- •Введение
- •1.Оптимальные методы
- •1.1.Методы поиска экстремумов функций
- •1.2.Учет ограничений на значения переменных
- •1.3.Использование Excel для поиска экстремумов функций
- •Лабораторная работа №1. Методы поиска экстремумов с помощью надстройки Поиск решения пакета Excel Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.Теория принятия решений
- •2.1.Основные понятия теории принятия решений
- •2.2.Математическая классификация задач разработки управленческого решения
- •2.3.Однокритериальная статическая задача разработки управленческого решения в условиях определенности
- •Лабораторная работа №2. Решение однокритериальной статической задачи в условиях определенности Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.4.Однокритериальная статическая задача разработки управленческого решения в условиях риска
- •Метод сведения задачи в условиях риска к детерминированной
- •Лабораторная работа №3. Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированной Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Методы оптимизации в среднем
- •Алгоритмический метод решения задачи в условиях риска
- •Лабораторная работа №4. Решение однокритериальной статической задачи в условиях риска алгоритмическим методом Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Метод Монте-Карло при решении задачи в условиях риска
- •Лабораторная работа №5. Решение однокритериальной статической задачи в условиях риска методом Монте-Карло Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Задачи в условиях риска с несколькими стохастическими параметрами
- •2.5.Однокритериальная статическая задача в условиях неопределенности
- •Игры с противником.
- •Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Игры с природой.
- •Лабораторная работа №7. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •Игры с природой с экспериментами.
- •Лабораторная работа №8. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.6.Многокритериальные задачи
- •Лабораторная работа №9. Решение многокритериальной задачи Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.7.Динамические задачи разработки управленческого решения Общая постановка динамической задачи разработки управленческого решения
- •Метод сетевого планирования
- •Методы теории массового обслуживания
- •Метод динамического программирования
- •Задача управления запасами
- •Методы вариационного исчисления и теории оптимального управления
- •Метод сведения дискретной динамической задачи к статической
- •Лабораторная работа №10. Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической Задание
- •Порядок выполнения работы
- •Контрольные вопросы
- •Отчет о работе
- •2.8.Рациональные решения Общий алгоритм разработки управленческого решения
- •Нереализуемые оптимальные решения
- •Разработка альтернатив для принятия рациональных решений
- •2.9.Экспертные методы Определение круга экспертов
- •Задачи, решаемые при проведении экспертизы
- •Разработка анкеты
- •Разработка методов обработки результатов
- •Проведение анкетирования, обработка и выдача результатов и принятие решения
- •Литература
- •Приложение а. Пример титульного листа отчета о выполнении лабораторной работы3.
- •Приложение б. Содержание отчетов о выполнении лабораторных работ Пример содержания отчета по лабораторной работе №2 «Решение однокритериальной статической задачи в условиях определенности»
- •Пример содержания отчета по лабораторной работе №3 «Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированной»
- •Пример содержания отчета по лабораторной работе №4 «Решение однокритериальной статической задачи в условиях риска алгоритмическим методом»
- •Пример содержания отчета по лабораторной работе №5 «Решение однокритериальной статической задачи в условиях риска методом Монте-Карло»
- •Пример содержания отчета по лабораторной работе №6 «Решение однокритериальной статической задачи в условиях неопределенности при играх с противником»
- •Пример содержания отчета по лабораторной работе №7 «Решение однокритериальной статической задачи в условиях неопределенности при играх с природой»
- •Пример содержания отчета по лабораторной работе №8 «Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами»
- •Пример содержания отчета по лабораторной работе №9 «Решение многокритериальной задачи»
- •Пример содержания отчета по лабораторной работе №10 «Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической»
- •Предметный указатель
Игры с природой с экспериментами.
Рассмотренные выше игры с природой предусматривали необходимость принятия нами решения в условиях неопределенности на основе имеющихся у нас данных, используемых в процессе вычислений. Такие данные принято называть априорными. В некоторых случаях при решении задач с природными неопределенностями появляется возможность проведения различных экспериментов, позволяющих получить дополнительную информацию и тем самым снизить степень неопределенности в отношении действительного состояния природы. Очевидно, что проведение экспериментов связано с затратой ресурсов. Возникают естественные вопросы: стоит ли проводить эксперимент, сколько должно быть экспериментов, в каком порядке надо проводить эксперименты. Некоторые ответы на эти вопросы дает теория игр с экспериментами.
Назовем единичным такой эксперимент, объем и порядок которого заранее определены и не могут быть изменены в процессе его проведения. Отметим, что собственно методику эксперимента должен разрабатывать специалист в предметной области, а мы можем только делать вывод о целесообразности его проведения на основании имеющейся априорной информации. Единичный эксперимент не обязательно состоит только из одного испытания. В процессе его проведения может быть получена целая выборка значений, однако принципиальным является то обстоятельство, что объем выборки конечен и известен заранее.
Возможен и другой способ организации эксперимента. В процессе проведения эксперимента после каждого испытания мы можем принимать решение, прекратить ли дальнейшие испытания и выбрать ли какую либо стратегию из числа возможных или продолжить испытания с целью увеличения объема информации. Такие эксперименты называют последовательными. Максимальное допустимое количество выборок в процессе проведения последовательного эксперимента тоже может быть известно заранее (в этом случае говорят об усеченном последовательном эксперименте), или быть неограниченным (неограниченный последовательный эксперимент).
Будем
считать, что в нашем распоряжении имеется
набор
стратегий
![]() ,
которые он может использовать в ответ
на одну из
возможных стратегий природы
,
которые он может использовать в ответ
на одну из
возможных стратегий природы
![]() ,
появляющуюся с вероятностью
,
появляющуюся с вероятностью
![]() при условии
при условии
.
Известна
также платежная матрица
![]() .
Для снижения неопределенности относительно
действительного состояния природы мы
можем провести эксперимент, стоимость
которого известна и равна
.
Для снижения неопределенности относительно
действительного состояния природы мы
можем провести эксперимент, стоимость
которого известна и равна
![]() .
Пусть в результате проведения эксперимента
состояние природы станет известно
точно. Необходимо сделать вывод о
целесообразности проведения эксперимента.
.
Пусть в результате проведения эксперимента
состояние природы станет известно
точно. Необходимо сделать вывод о
целесообразности проведения эксперимента.
Наш
средний выигрыш
![]() при использовании стратегии
может быть определен как
при использовании стратегии
может быть определен как
![]() .
(9)
.
(9)
В
качестве оптимальной стратегии может
быть выбрана стратегия
![]() ,
максимизирующая наш средний выигрыш
,
максимизирующая наш средний выигрыш
![]() .
.
Предположим теперь, что в результате проведения эксперимента удалось точно установить стратегию природы . Очевидно, что в этом случае мы должны выбирать стратегию, обеспечивающую наш максимальный выигрыш
![]() .
(10)
.
(10)
Оценим теперь средний возможный выигрыш после проведения эксперимента
![]()
где ‑ стоимость проведения эксперимента. Отсюда появляется условие целесообразности проведения эксперимента
![]()
или
![]() .
.
Преобразовывая неравенство, имеем
![]() .
(11)
.
(11)
Выражение в круглых скобках есть ничто иное как риск
![]() .
.
Тогда правая часть неравенства есть минимальный средний риск, откуда вытекает условие целесообразности проведения эксперимента: затраты на эксперимент должны быть меньше минимального среднего риска, иначе от эксперимента следует воздержаться и в качестве оптимальной следует выбрать стратегию максимизирующую средний выигрыш или минимизирующую средний риск.
Рассмотрим
случай, когда с помощью эксперимента
не удается точно определить состояние
природы, но возможно получить одно из
несовместимых событий
![]() ,
связанных определенными вероятностями
с состояниями (стратегиями) природы.
Обозначим условную вероятность появления
исхода
,
связанных определенными вероятностями
с состояниями (стратегиями) природы.
Обозначим условную вероятность появления
исхода
![]() эксперимента при условии стратегии
природы
эксперимента при условии стратегии
природы
![]() символом
символом
![]() .
Поскольку
образуют полную систему событий,
справедливо
.
Поскольку
образуют полную систему событий,
справедливо
![]() .
.
Будем
считать, что все значения
известны, а также известна стоимость
проведения эксперимента
.
Нас по прежнему будет интересовать
вопрос: целесообразно ли проведение
эксперимента и если да, то какую стратегию
необходимо выбрать при том или ином
исходе эксперимента. Предположим, что
в результате эксперимента был получен
результат
![]() .
Определим апостериорные вероятности
стратегий природы по теореме Байеса
[6]
.
Определим апостериорные вероятности
стратегий природы по теореме Байеса
[6]
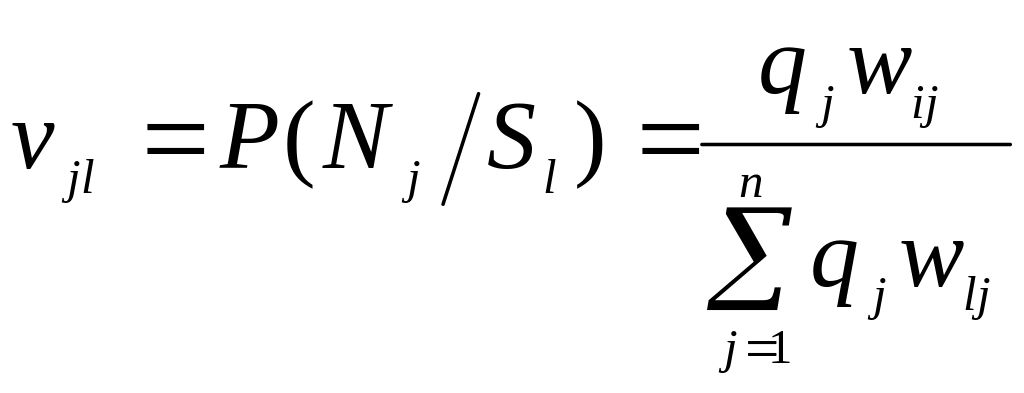 .
.
Далее для каждой стратегии рассчитаем величину условного среднего выигрыша при условии результата эксперимента
![]() .
.
Очевидно,
что оптимальной будет стратегия
![]() ,
обеспечивающая максимум условного
среднего выигрыша при конкретном исходе
эксперимента
,
обеспечивающая максимум условного
среднего выигрыша при конкретном исходе
эксперимента
![]() .
.
Вероятность
появления условного выигрыша
![]() совпадает с вероятностью появления
события
совпадает с вероятностью появления
события
![]() .
Обозначим ее символом
.
Обозначим ее символом
![]() .
Тогда
.
Тогда
![]() .
.
Величина выигрыша с использованием эксперимента
![]() .
.
С другой стороны наш выигрыш без проведения эксперимента определяется выражением
![]() .
.
Отсюда вытекает условие целесообразности проведения эксперимента
![]()
Если
проведение эксперимента признано
целесообразным, то необходимо разработать
систему так называемых решающих правил,
смысл которой сводится к следующему:
какую стратегию
![]() необходимо выбрать, если эксперимент
дал результат
?
необходимо выбрать, если эксперимент
дал результат
?
