10.2Анализ устойчивости типовых структур

Среди возможных структур связи между звеньями особо часто возникают некоторые простые структуры, которые будем называть типовыми. Все типовые структуры имеют внешний вход X и один внешний выход Y. К ним относятся последовательные и параллельные соединения звеньев, звенья с обратной связью.

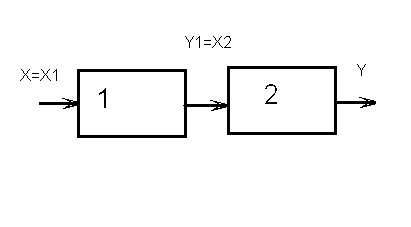
Вывод1 Последовательно соединенные звенья устойчивы, если устойчивы все составляющие звенья.

Вывод 2 Параллельно соединенные звенья устойчивы, если и только если устойчивы все составляющие звенья.

Вывод3 Система с обратной связью устойчива, если передаточная функция разомкнутой системы является правильной дробью, кроме того, передаточная функция ни при каких w от 0 до не является вещественным числом меньшим, либо равным -1.

Анализ устойчивости требуется рассмотренным методом.

10.3Понятие запаса устойчивости по амплитуде и фазе

При выполнении условий критерия Найквиста годограф может при этом не охватывать точку (-1;j0) “с запасом”. Оценим этот запас. Рассматривается отдельно запас по амплитуде и по фазе.

Рисунок 10‑31 Годограф Найквиста с запасом

Запас по амплитуде означает, что при увеличении коэффициента усиления на ΔА система станет неустойчивой.

Аналогично, при появлении дополнительного фазового сдвига Δϕ система также станет неустойчивой. Разные причины могут влиять на запасы устойчивости. В процессе проектирования гарантируются запасы устойчивости не ниже заданных. Таким образом, запасы устойчивости - есть данные на проектирование САУ.

Критерий устойчивости Найквиста может быть сформулирован с помощью логарифмических частотных характеристик, при этом и запасы устойчивости можно сформулировать также и на языке ЛАЧХ и ФЧХ. При этом определяются ΔLдб = 20lg(ΔА) и Δϕ.

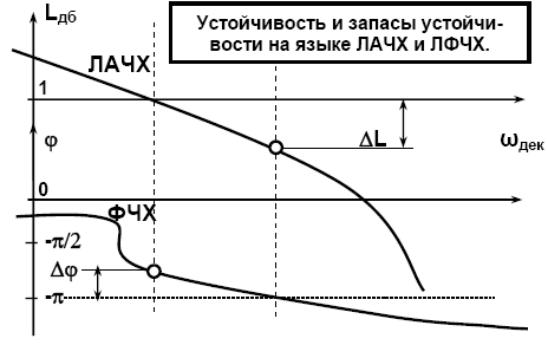
Рисунок 10‑32 Устойчивость и запасы устойчивости на языке ЛАЧХ и ЛФЧХ

где Δ А - запас по амплитуде; Δϕ - запас по фазе.

10.4Влияние звена чистого запаздывания на устойчивость

Чистое запаздывание – это часть системы (цепь или блок), при прохождении которой сигнал не меняет своей формы, но задерживается на время T.

Типичный пример: локальная сеть без потерь или длинная линия, или транспортная задержка.

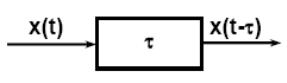
Покажем, что такому преобразованию соответствует передаточная функция; для этого вычислим преобразование Лапласа выходного сигнала:

Wзап(p)=e-pτ;

Таким образом, звену чистого запаздывания соответствует передаточная функция, не являющаяся дробно-рациональной. Она трансцендентная.

Рассмотрим АФЧХ - частотную характеристику звена чистого запаздывания:

При любом w получается точка единичной окружности.

АЧХ: |Wзап(jω)| = 1;

ФЧХ: ϕ(ω)= -ωτ;

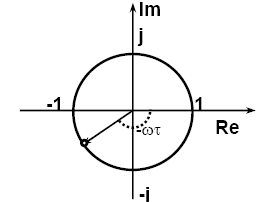
Рисунок 10‑33 Частотная характеристика

Видим, что звено чистого запаздывания добавляет отрицательный фазовый сдвиг, -1 1 чем больше, тем больше частота, тем самым уменьшая запас устойчивости по фазе. За счет этого сдвига система вполне может стать неустойчивой.

К сожалению, подобным образом нельзя описать запаздывание, зависящее от времени.

Фактически, мы ввели еще один стандартный блок, который можно было бы включить в стандартные звенья, если бы оно имело обычную, а не трансцендентную передаточную функцию. Полученное звено запаздывания формально является звеном бесконечного порядка, поэтому алгебраические методы исследования устойчивости системы, содержащей звенья запаздывания неприменимы.

Пример: Охватим инерционное звено ООС с запаздыванием на время τ.

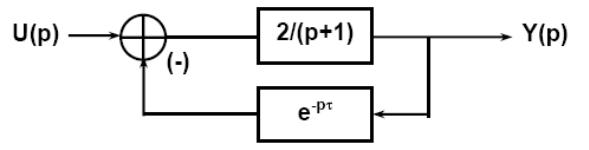
Рисунок 10‑34 Инерционное звено ООС с запаздыванием

Вычислим для замкнутой системы передаточную функцию и характеристический полином:

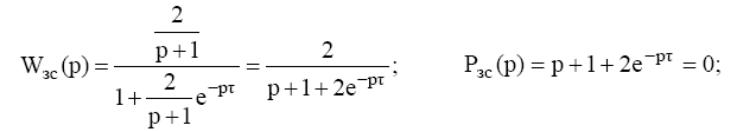
У такого характеристического полинома бесконечное число корней, среди которых могут быть и корни неустойчивые, поэтому численные методы становятся бессмысленными для обоснования устойчивости. Неприменимы критерий Гурвица и необходимое условие устойчивости, а вот частотные критерии устойчивости полностью применимы. Критерий Михайлова и, вытекающий из него критерий Найквиста, позволяют вполне корректно судить об устойчивости таких систем. Найдём АФЧХ разомкнутой системы.

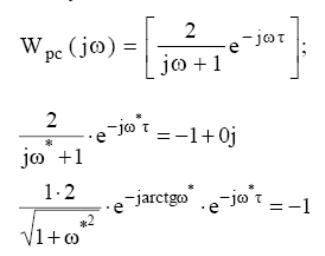
Как выяснить, при каком значении τ система (замкнутая) становится неустойчивой. Рассмотрим пограничный случай - прохождение через (-1;j0) на некоторой частоте ω*. Будем искать то минимальное значение времени запаздывания, при котором появляется неустойчивость. Подставляем АЧХ и ФЧХ инерционного звена и звена чистого запаздывания, решаем комплексное уравнение относительно ω*. Для этого приравняем по отдельности модуль и аргумент, для модуля имеется следующее равенство:

Для равенства аргументов требуется, чтобы sin(arctgω*-ω*τ)=0; Отсюда вытекает, что

Поэтому для τ получаем:

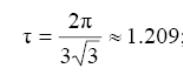
Это значение τ есть то минимальное запаздывание в нашей системе, при котором замкнутая система уже становится неустойчивой. Заметим, что звено запаздывания может располагаться и в прямой ветви, в данном случае все расчёты сохраняются.