
- •«Основы автоматики и систем автоматического управления
- •1Лекция №1 Введение
- •1.1Цель и задачи дисциплины, ее место в учебном процессе
- •1.2История развития сау
- •1.3Основные определения и термины
- •1.4Принцип обратной связи
- •1.5Система и ее среда
- •1.6Вопросы
- •2Лекция №2 Постановка задачи управления технологическими процессами производства рэс
- •2.1Рабочие операции и операции управления
- •2.2Понятие об объекте управления и управляющей подсистеме
- •2.3Постановка задачи
- •Вопросы
- •3Лекция №3 Решение задачи управления
- •3.1Решение общей задачи управления
- •3.2Частные решения задачи управления
- •3.3Вопросы
- •4Лекция №4 Сведения о технических средствах автоматики
- •4.1Сравнение биологических и технических систем управления
- •4.2Исполнительные устройства
- •Классификация технических задач управления
- •4.3Элементы системы автоматического управления технологическими процессами
- •4.4Устройства измерения параметров технологических процессов
- •4.5Различитель уровня
- •4.6Вопросы
- •5Лекция №5 Вторичные приборы сау
- •5.1Классификация вторичных приборов
- •5.2Усилительные устройства
- •5.3Проектирование и теория управления производственными процессами
- •5.4Вопросы
- •6Лекция №6 Математическое описание линейных систем автоматического управления
- •6.1Классификация систем
- •6.2Принцип суперпозиции
- •6.3Уравнения динамических систем
- •6.4Передаточные функции
- •6.5Частотные функции
- •6.6Временные характеристики сау. Понятие о функции Грина
- •6.7Вопросы
- •7Лекция №7 Типовые звенья сау
- •7.1Вопросы
- •8Лекция №8 Передаточные функции типовых звеньев
- •8.1Вопросы
- •9Лекция №9 Устойчивость линейных стационарных систем
- •9.1Понятие устойчивости
- •9.2Устойчивость по входу
- •9.3Характеристическое уравнение
- •9.4Необходимое и достаточное условие устойчивости
- •9.5Условие строгой реализуемости передаточной функции
- •9.6Алгебраические критерии устойчивости
- •9.7Критерий устойчивости Гурвица
- •9.8Критерий Льенара
- •9.9Критерий устойчивости Рауса
- •9.10 Вопросы
- •10Лекция № 10 Частотные критерии устойчивости
- •10.1Критерий Михайлова
- •10.2Анализ устойчивости типовых структур
- •10.3Понятие запаса устойчивости по амплитуде и фазе
- •10.4Влияние звена чистого запаздывания на устойчивость
- •10.5Вопросы
- •11Лекция №11 Основы анализа качества линейных стационарных сау
- •11.1Постановка задачи
- •11.2Показатели качества переходного процесса
- •11.3 Интегральные показатели качества
- •11.4Вопросы
- •12Лекция №12 Анализ точности работы линейной системы автоматического управления
- •12.1Случайные процессы в линейных стационарных системах
- •12.2Вопросы
- •13Лекция №13 Полигауссовы модели случайных воздействий и методы их анализа
- •13.1Дифференцирующее звено
- •13.2Средняя квадратическая ошибка системы
- •13.3Вопросы
- •14Лекция №14 Синтез линейных стационарных систем
- •14.1Проектирование сау
- •14.2Синтез линейных систем методом частотных характеристик
- •14.3Вопросы
- •15Лекция №15 Расчет передаточных функций корректирующих устройств
- •15.1Вопросы
- •16Лекция № 16 Синтез сау методом логарифмических частотных характеристик
- •16.1 Общие замечания
- •16.2Синтез сау методом логарифмических частотных характеристик
- •16.3Подчиненное управление в сау
- •Примечание:
- •16.4 Модальное управление в сау
- •16.5 Вопросы
- •17Лекция № 17 Синтез систем с неполной информацией о входных воздействиях
- •17.1Ограничение суммарной ошибки
- •17.2Вопросы
13.2Средняя квадратическая ошибка системы
Количество работы систем автоматического управления при случайных воздействиях оценивается по суммарной средней квадратической ошибке.
Для большинства случаев, когда закон распределения системы можно считать Гауссовским, при расчете составляющих суммарной средней квадратической ошибки, достаточно учесть математическое ожидание и корреляционную функцию ошибки, или ее спектральную плотность.
На вход системы подается воздействие вида:
![]()
где x(t) – случайный сигнал;
n(t) – случайная помеха.

Рисунок 13‑46 Воздействие случайных сигналов и помех
Суммарная ошибка системы при этом равна:
![]()
проведем преобразование Лапласа:
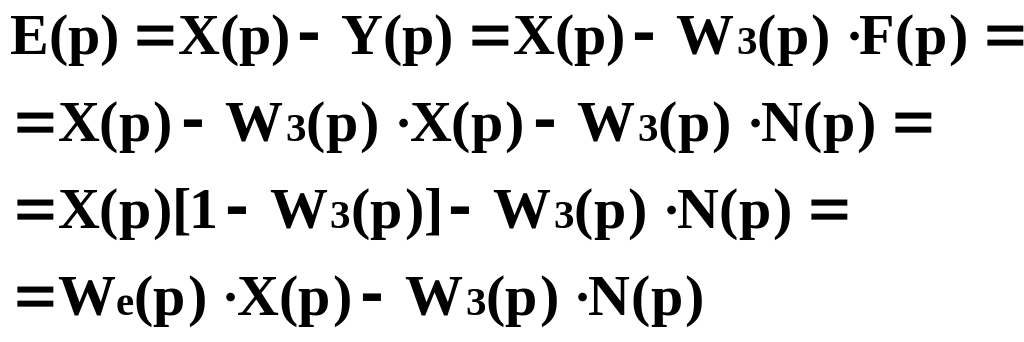
где W3(p)- передаточная функция замкнутой системы;
We(p)- передаточная функция ошибки анализируемой системы.
Таким образом, суммарная ошибка состоит из двух составляющих, одна из которых зависит от передаточной функции ошибки и определяет точность воспроизведения сигнала, а вторая обусловлена действием помехи и зависит от передаточной функции замкнутой системы.
Рассмотрим ситуацию, когда сигнал и помеха являются стационарными случайными функциями. При этом будем считать математическое ожидание помехи равным нулю, а случайный сигнал представим как:
![]()
где mx - математическое ожидание сигнала;
![]() -
случайные составляющие сигнала.
-
случайные составляющие сигнала.
Математическое ожидание суммарной ошибки можем записать как:
![]()
Дисперсия ошибки зависит от случайных составляющих сигнала и помехи:
![]()
где e- средняя квадратическая ошибка системы;
e(t) - ошибка системы;
М – математическое ожидание от квадрата ошибки.
Первое слагаемое зависит от передаточной функции ошибки и от статистических характеристик сигнала. Оно определяет среднюю квадратическую ошибку воспроизведения сигнала x(t). Второе слагаемое зависит от передаточной функции замкнутой системы и характеристик помехи. Оно характеризует ошибку системы вследствие действия помехи n(t).
Последние два слагаемых – составляющие ошибки из-за корреляции сигнала с помехой и помехи с сигналом.
![]()
На практике часто встречаются случаи, когда помеху можно считать белым шумом, тогда спектральная плотность ее в пределах полосы пропускания САУ постоянна.
Эффективная полоса пропускания системы равна:
![]() ,
,
где wэф – основание прямоугольника, площадь которого равна площади, ограниченной графиком АЧХ.
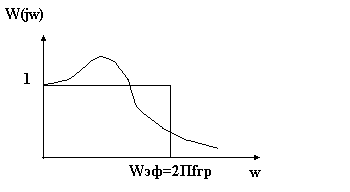
Рисунок 13‑47 Эффективная полоса пропускания системы
Помехи обычно являются белыми шумами, а сигналы, как правило, не относятся к белым шумам. Однако, если использовать формирующий фильтр, то анализ системы, относительно сигналов, сводится к случаю действия на систему белых шумов.
Формирующий фильтр – устройство, позволяющее генерировать сигнал с заданной спектральной плотностью из сигнала белого шума.
Формирующий фильтр и анализируемая система образуют некоторую расширенную систему, на вход которой действует белый шум.
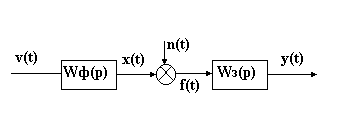
Рисунок 13‑48 Формирующий фильтр
Если помеха - не белый шум, то в схему нужно также включить формирующий фильтр, который из белого шума будет генерировать случайную помеху с заданной спектральной плотностью.
