10Лекция № 10 Частотные критерии устойчивости
Частотными критериями называются критерии устойчивости, основанные на построении частотных характеристик. Запишем знаменатель передаточной функции.
Подставляя в него
получаем.
Кривую, которая описывает конец вектора
на комплексной плоскости при изменении
от 0 до
называют
кривой Михайлова.
10.1Критерий Михайлова
Для того чтобы система была устойчива необходимо и достаточно, чтобы кривая Михайлова, начинаясь при a0>0 с действительно положительной полуоси, при возрастании последовательно обходила n квадрантов, в положительном направлении, не попадая в начало координат (рис. 8-1).
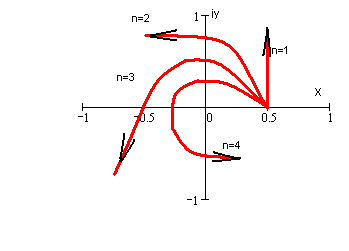
Рисунок 10‑27 Годограф Михайлова
Пример: Характеристический полином.
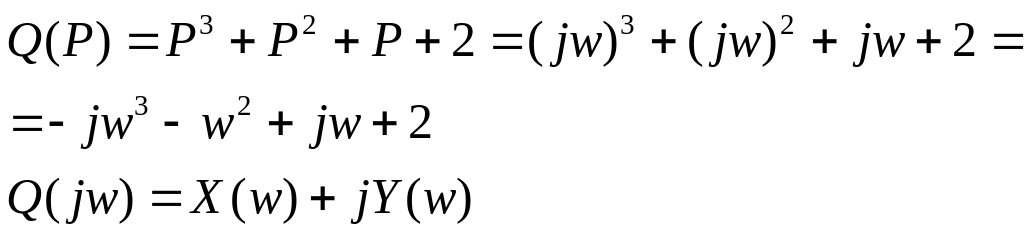
Составим таблицу
w |
0 |
0<w<1 |
1 |
1<w< |
w> |
|
X(w) |
2 |
>0 |
1 |
>0 |
<0 |
|
Y(w) |
0 |
>0 |
0 |
<0 |
<0 |
|
Построим кривую Михайлова. В пределах квадранта всей кривой Михайлова на устойчивость не влияет, и она строится приблизительно. Система неустойчива, т.к. кривая не охватывает последовательно 1, 2, и 3 квадрант.
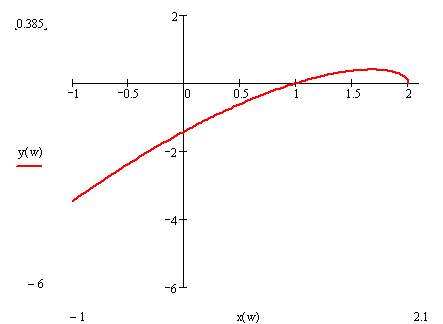
Рисунок 10‑28 – Годограф Михайлова
Пример.
Характеристический многочлен
Для
имеем
,
Составим таблицу
w |
0 |
0<w< |
|
<w<1 |
1 |
w>1 |
|
X(w) |
0,5 |
>0 |
0 |
<0 |
-0,5 |
<0 |
|
Y(w) |
0 |
>0 |
0,35 |
>0 |
|
<0 |
|
Построим кривую Михайлова
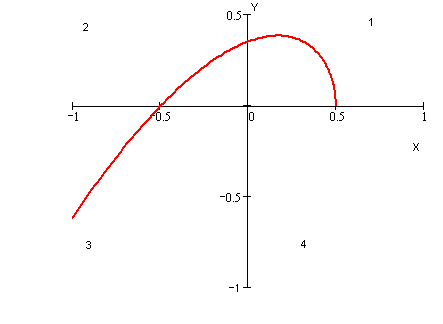
Рисунок 10‑29 Годограф Михайлова
Кривая последовательно охватывает все 3 квадранта, следовательно, система будет устойчивой.
Алгебраические критерии устойчивости и критерий Михайлова применимы для исследования замкнутой и разомкнутой систем.
Есть критерий, который предназначен для исследования лишь замкнутых систем. Этот критерий был сформулирован Найквистом.
Критерий Найквиста
Пусть l из корней разомкнутой системы находится в правой полуплоскости, а остальные n-l в левой полуплоскости. Тогда, для того, чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика её разомкнутой системы с ростом w от 0 до охватывала точку (-1,j0) в положительном направлении, т.е. против движения часовой стрелки в (l /2) раз.
В частности, если разомкнутая система устойчива (и, следовательно, l=0), то для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика её разомкнутой системы охватывала точку (-1, j0) в положительном направлении l/2 раза.
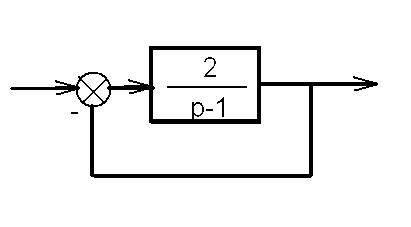
Пример: частотная передаточная функция
её разомкнутой системы
Составим таблицу.
w |
0 |
w>0 |
|
U(w) |
-2 |
<0 |
|
V(w) |
0 |
<10 |
|
Рисунок 10‑30 Годограф Найквиста
Амплитудно – фазовая частотная характеристика разомкнутой системы охватывает точку (-1, j0) в положительном направлении ½ раза. Характеристическое уравнение разомкнутой системы имеет 1 корень, т.е. l=1, поэтому замкнутая система устойчива.
Примеры:
Варианты:
a0 |
a1 |
a2 |
a3 |
1 |
1 |
2 |
2 |
3 |
2 |
1 |
2 |