§2. Первое начало термодинамики

Поскольку внутренняя энергия системы может изменятся двумя способами ― путём совершения работы и путём передачи ей некоторого количества тепла, то в соответствии с законом сохранения энергии можно утверждать, что количество теплоты δQ, сообщаемое системе идёт на увеличение внутренней энергии dU и на работу δА, совершаемую системой над телами:

(92)

δQ = dU + dA

В отличие от закона сохранения и превращения механической энергии в первом начале термодинамики рассматривается изменение энергии системы не только за счёт совершения работы, но и за счёт передачи тепла.

Отметим, что δQ считается положительным, если тепло получается системой, и отрицательным, если система отдаёт тепло окружающей среде. Наоборот, δА считается положительным, если система совершает работу против внешних сил, и отрицательным в противоположном случае.

Уравнение (92) записано для бесконечно малого изменения состояния системы, т.е. в дифференциальной форме. Проинтегрируем (92) от состояния 1 до состояния 2, испытанного системой частиц.

Если обозначить через ― количество теплоты, полученное системой при переходе из состояния 1 в состояние 2, через ― работу, произведенную системой при этом переходе и, наконец, через ― изменение внутренней энергии системы при том же переходе, то выражение первого начала термодинамики в интегральной форме примет вид:

(93)

Следует также отметить, что под работой, совершаемой системой, подразумевается не только работа сил, обычно рассматриваемых в механике, но и работа сил любой природы. Например, это может быть работа электрических, магнитных сил, работа сил поверхностного натяжения и т.д.

В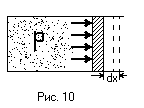 дальнейшем под работой будет подразумеваться работа, совершаемая системой частиц, при изменении объёма этой системы. Пусть системой является газ, находящий в цилиндре, который закрыт подвижным поршнем площадью S (Рис. 10). При бесконечно малом расширении газа, т.е. при увеличении его объёма на dV, газ совершает работу над поршнем, равную произведению силы, действующей со стороны газа на поршень F=PS, на бесконечно малое перемещение поршня dx:

(94)

Таким образом, элементарная работа, совершаемая газом, равна произведению давления, под которым находится газ, на бесконечно малое изменение его объёма.

Работа, совершаемая газом, при конечном изменении объёма:

(95)

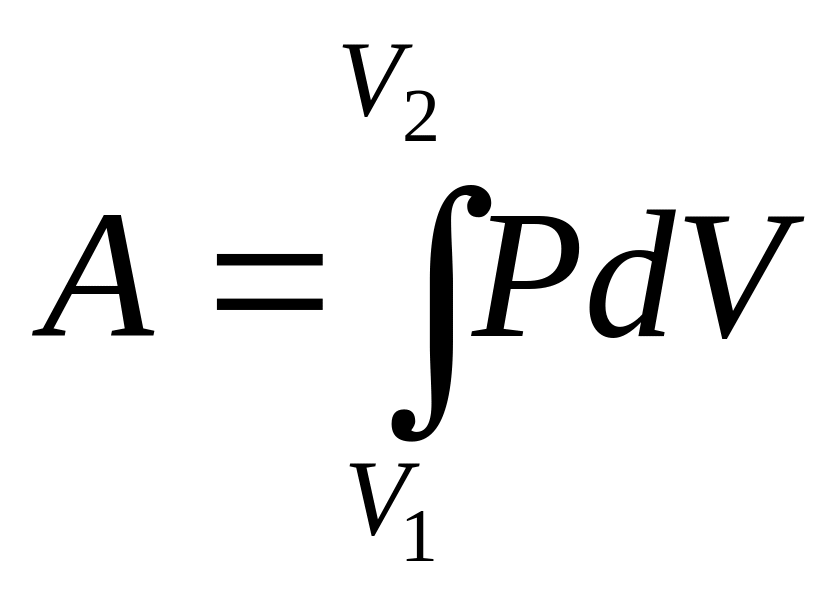
Если при изменении объёма давление газа было постоянным (P=Const), то A=P(V₁ – V₂), т.е. при изобарическом расширении работа, производимая газом, равна произведению давления на изменение объёма.

В случае произвольной зависимости P=P(V) работа расширения (сжатия) газа от объёма V₁ до V₂ объёма существенно зависит не только от V₁ и V₂, но и от пути перехода. Если переводить систему из состояния 1 в состояние 2 по пути 1А2, то работа, в соответствии с (95), будет равна величине площади под кривой 1А2 (Рис.11), если же ― по пути 1В2, то будет равна меньшей площади, равной площади под кривой 1В2. Физически это объясняется тем, что давление газа Р зависит не только от объёма V, но и от температуры Т. Поэтому, меняя по-разному температуру при переходе из 1 в 2, получаем различные по форме линии, изображающие процессы перехода из состояния 1 в состояние 2 (при переходе 1В2 температура газа всё время остаётся меньше, чем при переходе 1А2).

В математическом анализе доказывается, если величина криволинейного интеграла не зависит от формы пути интегрирования, то подынтегральная функция является полным дифференциалом некоторой функции. В нашем случае подынтегральная функция в выражении работы (95) δА=PdV не является полным дифференциалом и обозначается δА, а не dA, так как величина интеграла (95) зависит от пути. Изменение же внутренней энергии, как отмечалось ранее, не зависит от пути и определяется разностью её значений в состояниях 2 и 1, т. е.

(96)

и, таким образом, подынтегральная функция dU ― полный дифференциал.

Из первого начала термодинамики

(97)

следует, если величина (dU+δA), стоящая в правой части (97) не является полным дифференциалом, то и его левая часть δQ не есть полный дифференциал.

Таким образом, зависимость величин A и Q от пути перехода системы из одного состояния в другое означает, что работа и количество теплоты не являются функциями состояния системы. Они характеризуют не состояние системы, а процесс изменения этого состояния, и если нет процесса, то ни работы, ни теплоты у системы тоже нет, в то время как внутренняя энергия всегда существует. Поэтому величина δA есть просто элементарная работа, совершаемая системой при бесконечно малом изменении состояния (но не изменения работы); аналогично δQ означает бесконечно малое количество теплоты, переданное системе (но не изменения количества теплоты). Величина же dU есть бесконечно малое изменение внутренней энергии, являющейся функцией состояния системы.