3.Методи прогнозування часових рядів: методи соціально - економічного прогнозування.

Прогноз – це науково-обгрунтоване судження стосовно можливих станів об’єктів майбутнього, альтернативні шляхи і терміни їх здійснення. Має випадковий характер, але, оскільки він будується на підставі науково-обгрунтованих уявлень про стан і розв’язок об’єкта, здійснення його є в надані ймовірності.

Прогноз оцінюється як очікуваний ймовірний стан об’єкта в майбутньому.

Процес розроблення прогнозів наз прогнозуванням.

Необхідність прогнозувати розвиток тієї чи іншої ситуації, майбутніх змін тих чи інших обставин ставлять дослідників перед проблемою вибору конкретного методу прогнозування.

Методи соціально-економічного прогнозування:

1. Кількісні методи:

• Каузальні: багатомірні регресійні моделі; економетричні моделі; комп’ютерна імітація. Застосовуються в тих випадках, коли шуканий стан залежить не тільки від часу, а й від багатьох змінних.

• Аналіз часових рядів: оснований на припущенні у відповідності з яким, те. Що відбулося в минулому, дає гарне наближення в оцінці майбутнього, і є способом виявлення тенденцій минулого та їх продовження в майбутнє.

2. Якісні методи

Білет №24

1. Основні задачі економетрії.

Найважливішою задачею є оцінювання параметрів і перевірка значущості економетричної моделі. Першим етапом цього процесу є специфікація моделі в математичній формі. Другий етап — збір і підготовка економічної інформації. На третьому етапі оцінюються параметри моделі. Четвертий етап — це перевірка моделі на вірогідність. Дуже важливими на цьому етапі є оцінки дисперсії залишків моделі. Ці оцінки відіграють вирішальну роль при з’ясуванні якості економетричних моделей, вони необхідні для визначення надійності обчислених параметрів і для застосування розроблених моделей у прогнозуванні.

1. Дослідження розвитку економічних процесів і прогнозування, їх динаміки

2. Правильний вибір факторів при побудові математично-статистичної моделі

3. Вибір і побудова матем-статист моделі, здійснення ряду модельних експериментів, аналіз одержаних результатів і перенесення їх на реальну економічну систему як основу прийняття незалежних рішень.

2. Емпірична модель множинної лінійної регресії.

На будь-який економічний показник Y, як правило, впливає не один, а декілька факторів (регресорів) .

В подібних випадках маємо справу з множинною лінійною моделлю (регресією), що описує взаємний зв’язок між залежною змінною Y та регресорами і яку можна подати такому вигляді:

Загальний запис теоретичної лінійної множинної регресії може бути зроблений в такому вигляді:

(16.1)

де – теоретичні коефіцієнти регресії (часткові коефіцієнти); – вільний член; – значення -го регресора при і-ому спостереженні; – випадковий збудник.

Для однозначного визначення параметрів моделі необхідно, щоб виконувалась нерівність де n – число спостережень; m – число регресорів

У векторно-матричній формі теоретичну модель можна подати так: (16.2) де

Якщо теоретичний вектор є величиною сталою і нам невідомою, то емпіричний вектор ми можемо визначити шляхом обробки статистичної інформації вибірки обсягом n. Враховуючи те, що вибірка складає лише незначну частину генеральної сукупності (n≤N), то інформація, яку одержимо при статистичній обробці, про регресори X_j моделі буде не повною і для кожної іншої вибірки буде потерпати певні зміни. 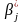Отже, компоненти емпіричного вектора будуть містити елемент випадковості. Таким чином, , як і сам вектор будуть випадковими величинами, які мають певні закони розподілу ймовірностей із відповідними числовими характеристиками.

Із вище наведеного можемо тепер стверджувати, що є статистичною оцінкою для теоретичного вектора . А тому постають питання математичної статистики: зміщена чи незміщена ця статистична оцінка; в якому довірчому інтервалі із заданою надійністю γ можуть перебувати теоретичні компоненти (параметри) і сама функція регресії; як здійснити перевірку на статистичну значущість теоретичних параметрів по заданому рівню значущості α.

Для вирішення цих питань нам необхідно визначити числові характеристики для параметрів (j=0,1,2,...,m) і для самої функції регресії, використовуючи при цьому елементи матричної алгебри як інструментарію, застосовуючи який ми можемо без громіздких викладок отримати необхідні результати.