1.7. Обобщенный метод наименьших квадратов

При нарушении гомоскедастичности остатков и наличии их автокорреляции применяется обобщенный МНК по отношению к преобразованным данным. Этот метод позволяет получить не только несмещенные оценки, но и оценки, имеющие наименьшую выборочную дисперсию.

Для корректировки гетероскедастичности выполняется следующее преобразование:

,

где – дисперсия ошибки при -том значении фактора;

– постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;

коэффициент пропорциональности: меняется с изменением величины фактора, характеризуя неоднородность дисперсии.

Предполагается, что неизвестна, а в отношении выдвигаются гипотезы, характеризующие структуру гетероскедастичности.

Для линейного уравнения модель примет вид , в которой остатки гетероскедастичны. Предполагая в них отсутствие автокорреляции остатков, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные на , тогда дисперсия остатков будет постоянной ( ).

Таким образом, от регрессии Y по X переходят к регрессии по преобразованным величинам и .

Уравнение регрессии примет следующий вид:

.

Исходные данные для построения регрессии можно представить как

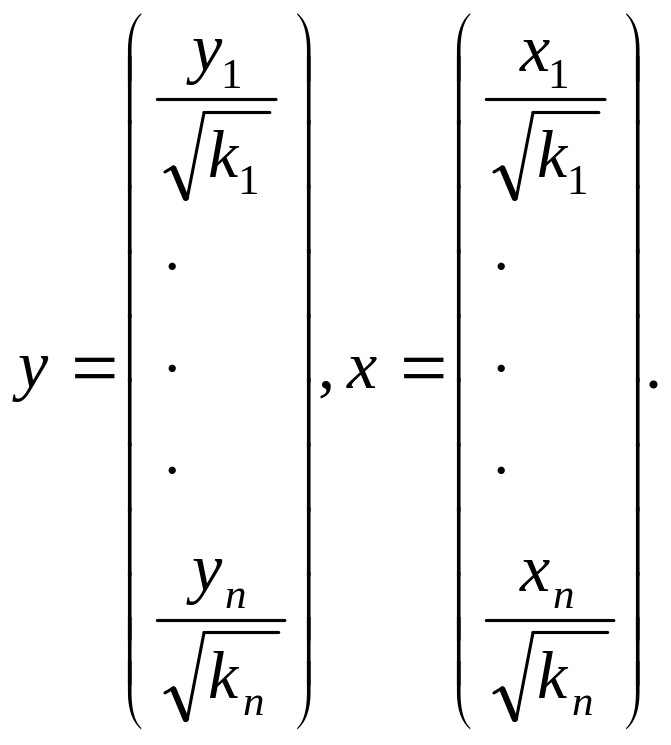
Отличие обычного МНК от обобщенного МНК, следовательно, заключается в том, что уравнение регрессии с новыми переменными по отношению к обычной регрессии представляет собой взвешенную зависимость с коэффициентом .

Оценка параметров нового уравнения осуществляется по взвешенному критерию следующего вида:

2. Множественная корреляция и регрессия

Основная цель множественного корреляционно-регрессионного анализа заключается в построении модели как можно с большим числом факторов, а также – в определении влияния каждого из них в отдельности и в совокупности на изменение результативного показателя.

2.1. Множественный корреляционный анализ

Множественный корреляционный анализ решает две задачи.

Во-первых, это исследование взаимосвязи одной переменной с совокупностью всех остальных переменных.

Во-вторых, это изучение зависимости между двумя переменными при исключении (элиминировании) влияния всех остальных переменных.

Эти задачи решаются на основе матрицы парных коэффициентов корреляции следующего вида:

.

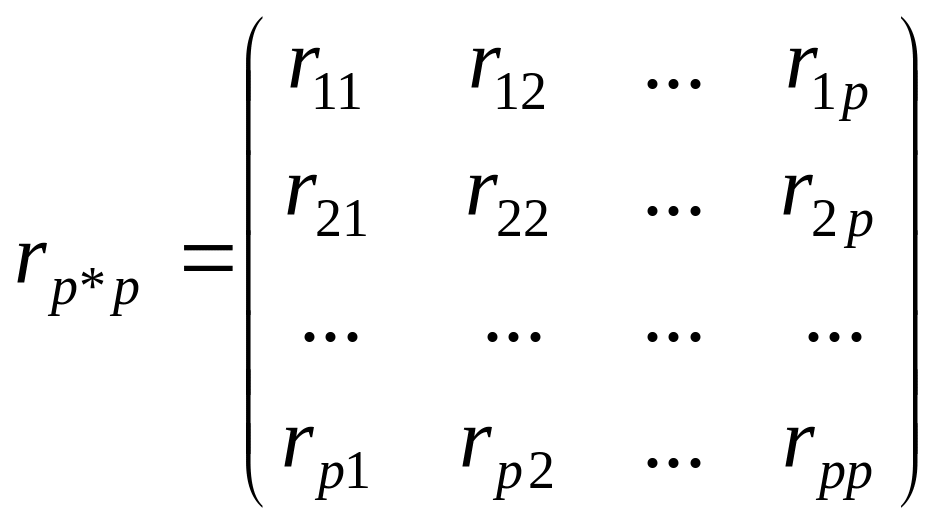Заполнение матрицы упрощается за счет учета свойств парных коэффициентов корреляции, а именно:

• влияния факторов самих на себя является функциональным, т.е. ;

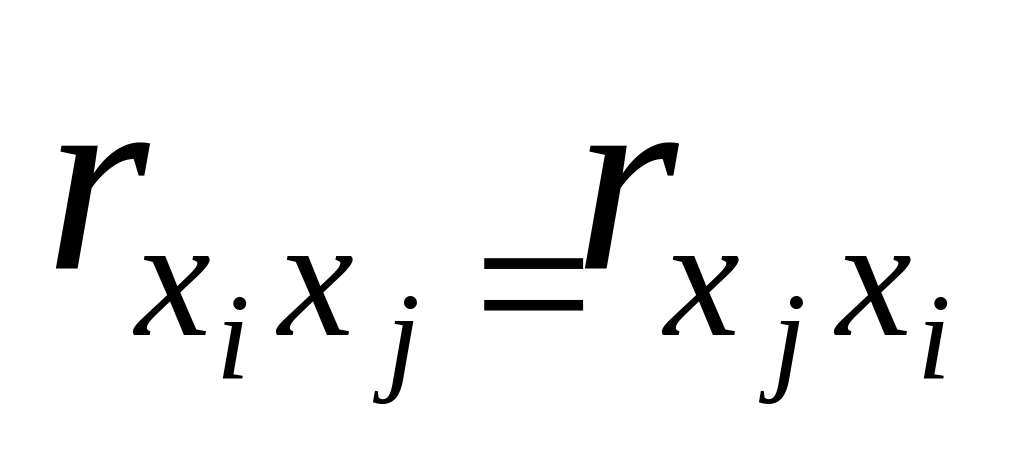• , т.е. матрица симметрична относительно главной диагонали.

Первая задача решается путем расчета и проверки значимости коэффициента множественной корреляции, определяемого по формуле

, (2.1)

где – определитель матрицы ;

алгебраическое дополнение элемента той же матрицы.

Коэффициент множественной корреляции не меньше, чем абсолютная величина любого парного или частного коэффициента корреляции, взятого с тем же первичным индексом.

Величина называется выборочным множественным коэффициентом детерминации, который численно оценивает долю вариации исследуемой переменной, объясняемую изменением (вариацией) всех остальных факторов.

Значимость множественной корреляции доказывается выполнением следующего условия (по F-распределению Фишера):

, (2.2)

где – объем выборки;

– количество факторов;

и – числа степеней свободы, равные и соответственно.

Вторая задача решается путем расчета и проверки значимости выборочного частного коэффициента корреляции, определяемого по формуле:

, (2.3)

где – алгебраические дополнения элементов матрицы парных коэффициентов корреляции соответственно.

Свойства частных коэффициентов корреляции аналогичны свойствам парного коэффициента корреляции (п.1.2). Проверка значимости также осуществляется на основе t-критерия Стьюдента, но число степеней свободы принимается равным .