1.3. Нелинейная регрессия
Выделяют следующие группы нелинейных уравнений регрессии.
Во-первых, это регрессия, нелинейная относительно факторов (объясняющих переменных), но линейная по оцениваемым параметрам. Примерами таких моделей могут быть следующие функции:
–
парабола второго
порядка;
– парабола третьего
порядка;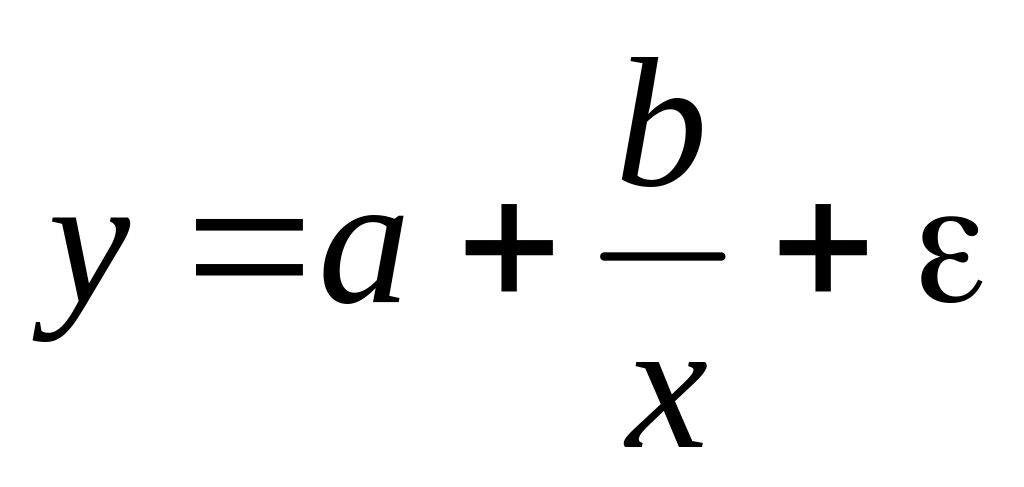
– гипербола.
Параметры данных
моделей, как и в линейной регрессии,
оцениваются обычным МНК, т.к. эти функции
линейны по параметрам. Например, в
параболе второй степени, заменяя
переменные
,
получим двухфакторное уравнение
регрессии
.
К следующей группе относят регрессию, нелинейную по оцениваемым параметрам. В ее составе выделяют две подгруппы.
В одну из них
включают нелинейные модели, которые
являются внутренне линейными, т.е. те,
которые могут быть линеаризованы.
Например, степенную функцию
необходимо прологарифмировать как
Для линеаризации
обратной модели вида
находится величина, равная
.
Возможно одновременное использование
логарифмирования и нахождения обратных
величин (в частности, для логистической
функции
).
Параметры моделей данной подгруппы оцениваются с помощью МНК после их линеаризации, при этом меняется критерий оценки параметров [4]. В частности, он может принять следующий вид:
.
Ко второй подгруппе
относят модели, которые можно считать
внутренне нелинейными. Эти функции
не могут быть приведены к линейному
виду. Например,
и
.
Линеаризация таких моделей невозможна. Поэтому обычный МНК неприменим, а для оценки параметров используются итеративные процедуры, точность которых зависит от конкретного вида уравнений регрессии и от особенностей используемого численного метода.
1.4. Проверка значимости линейного уравнения регрессии
Значимость уравнения определяется возможностью надежного прогноза результативного показателя по значениям факторных признаков. Значимость линейной регрессии проверяется по F–критерию Фишера, расчетное значение которого определяется согласно следующей формуле:
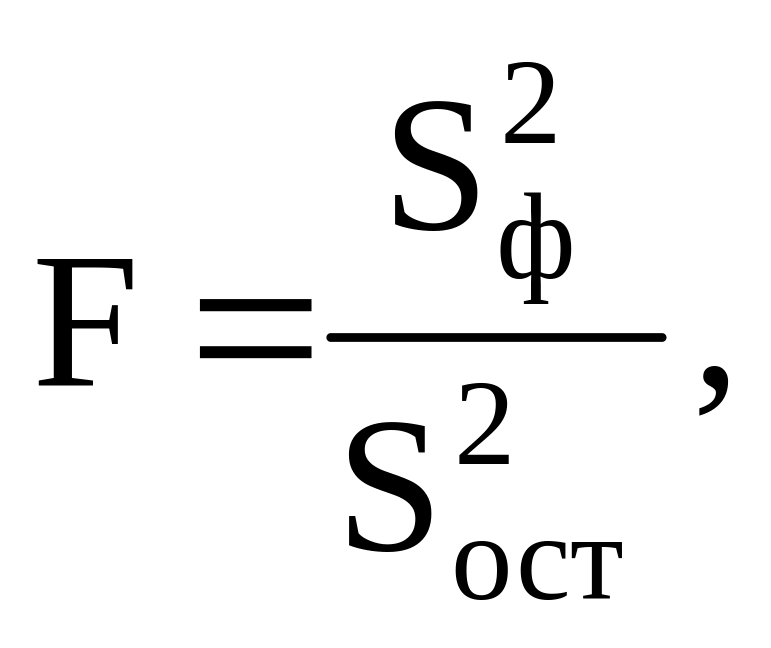(1.8)
где
–
факторная
дисперсия результативного показателя
(оценивает степень влияния изучаемого
фактора на Y,
т.е.
объясняемую регрессию), которой
соответствует число степеней свободы
,
;
(1.9)
–
остаточная
дисперсия (характеризует воздействие
неучтенных факторов, т.е. необъясняемую
регрессию):
(1.10)
где
–
число степеней свободы, соответствующее
линейной регрессии.
Если
расчетное значение критерия больше
табличного, выбираемого по теоретическим
значениям F-распределения
Фишера при заданном уровне значимости
и двух степенях свободы
и
,
то выдвинутая гипотеза о незначимости
линейного уравнения регрессии не
принимается.
Для выбора лучшего уравнения регрессии (из множества значимых) могут быть использованы следующие критерии их качества:
минимум остаточной дисперсии;
минимум корреляционного отношения
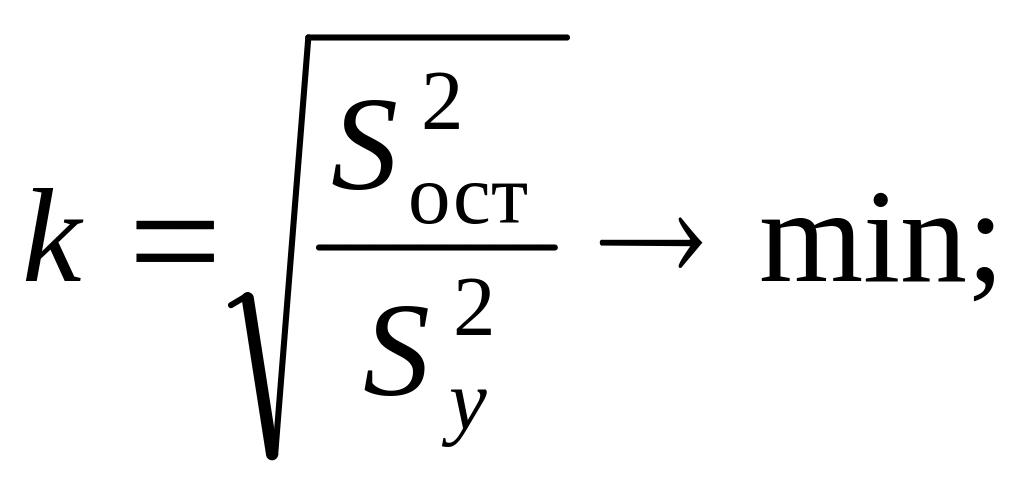(1.11)
минимум относительной ошибки аппроксимации
.
(1.12)
Уравнения регрессии затем ранжируются по данным критериям. Минимальная сумма баллов соответствует лучшему уравнению регрессии [2].
Оценивается
значимость не только уравнения в целом,
но и отдельных его параметров путем
расчета их стандартных ошибок. Например,
для линейной регрессии вида
истинные значения параметров от
рассчитанных по выборочным данным
отличаются на следующие величины
стандартных ошибок
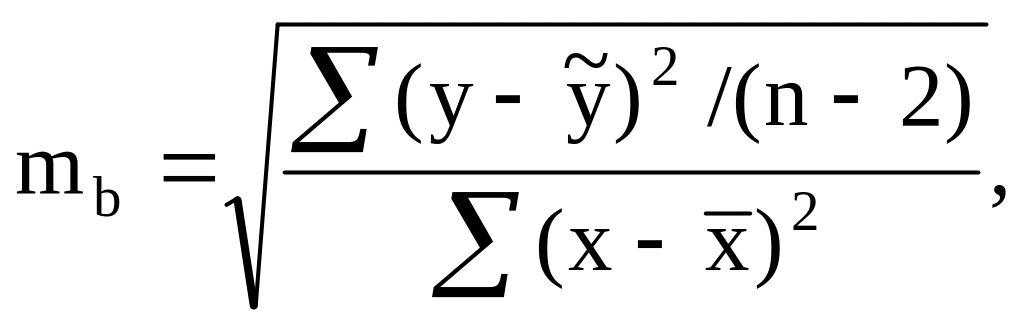
Доверительные
границы Y
при значении фактора
для линейной регрессии определяются
по формуле
(1.13)
где
–
значение Y,
рассчитанное по уравнению регрессии
при
;
–
табличное значение
критерия Стьюдента при уровне значимости
и числе степеней свободы
.