5.2.2. Выбор вида пространственно-динамической модели
Перечисленные способы построения обобщенных моделей можно использовать только при несущественном изменении характера связи между показателями во времени, что проявляется в близости соответствующих параметров одногодичных уравнений (5.1). Для определения значимости построенной модели (5.2) проверяются две гипотезы:
о
стабильности коэффициентов связи
,
;
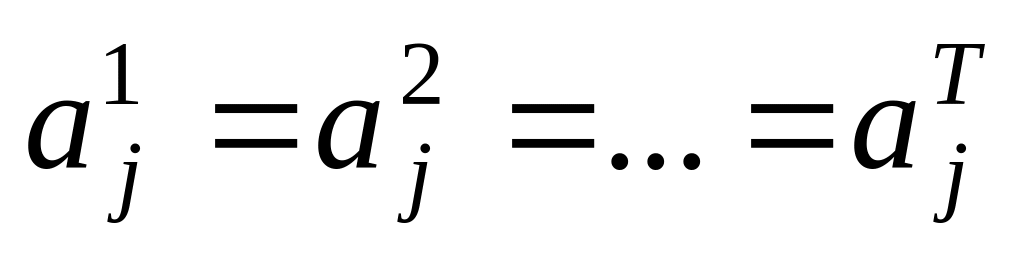о
стабильности свободных коэффициентов
.
Если обе гипотезы
не отвергаются, то построение обобщенной
модели допустимо. Если гипотеза
не отвергается,
а гипотеза
отвергается, то изменения в структуре
связи могут быть объяснены динамикой
влияния неучтенных факторов и воздействием
фактора времени, что и отражается в
свободных числах
.
При этом уравнение связи признаков
различных лет
(5.3)
отличается только
параметрами
Модель (5.3) называют
обобщенным
уравнением связи с годовыми эффектами.
Для проверки выдвинутых гипотез рассчитываются следующие величины
,
,
,
где – фактические значения результирующего показателя в период времени t;
–
значения, вычисленные
по одногодичным уравнениям (5.1);
–
расчетные значения
по обобщенному уравнению связи (5.2);
– значения
результативного признака, вычисленные
по обобщенному уравнению регрессии с
учетом годовых эффектов (5.3).
Величина
вычисляется при различных значениях
коэффициентов регрессии и свободных
членов;
определяется при условии равенства
всех параметров уравнения;
оценивается при равенстве коэффициентов
регрессии и возможном различии свободных
чисел. В связи с этим для проверки
гипотезы
вычисляется дисперсия потерь в результате
использования для всех периодов времени
одинаковых величин
(
)
и остаточная дисперсия, полученная в
результате построения одногодичных
уравнений регрессии (
),
,
.
Величина
имеет F-распределение
со степенями свободы
и
.
Расчетное значение сравнивается с
табличной величиной
.
Если расчетное значение больше табличного,
то гипотеза
при
данном уровне значимости
отвергается. Следовательно, коэффициенты
одногодичных уравнений различаются, и
изменение структуры связи нельзя
объяснить изменением свободных чисел.
Иначе (неравенство не выполняется) –
гипотеза
не отвергается,
т.е. коэффициенты связи в одногодичных
уравнениях могут быть одинаковыми
(структура связи не меняется).
Для проверки гипотезы вычисляются дисперсии
,
.
Величина
в этом случае имеет F-распределение
со степенями свободы
и
.
Если расчетное значение больше табличного
,
то гипотеза
при данном уровне значимости
отвергается, т.е. изучаемая зависимость
не может моделироваться обобщенным
уравнением (5.2). Иначе – возможно
построение данного уравнения.