
- •Содержание
- •Введение
- •1. Парная корреляция и регрессия
- •1.1. Спецификация модели
- •1.2. Линейная корреляция и регрессия
- •1.3. Нелинейная регрессия
- •1.4. Проверка значимости линейного уравнения регрессии
- •1.5. Корреляция для нелинейной регрессии
- •1.6. Предпосылки метода наименьших квадратов
- •1.7. Обобщенный метод наименьших квадратов
- •2. Множественная корреляция и регрессия
- •2.1. Множественный корреляционный анализ
- •2.2. Спецификация модели
- •2.3. Частные уравнения регрессии
- •2.4. Выбор формы уравнения множественной регрессии
- •Оценка параметров уравнения множественной регрессии
- •2.6. Многошаговый регрессионный анализ
- •3.1.2. Способы выявления структурной неоднородности
- •3.2. Методы последовательного разбиения
- •3.3. Методы многомерной классификации
- •3.3.1. Мера сходства
- •3.3.2. Модели кластерного анализа
- •4.2. Числовые характеристики экономического развития
- •4.3. Состав динамического ряда
- •4.4. Моделирование одномерных динамических рядов
- •4.4.1. Типы экономического развития и их трендовые модели
- •4.4.2. Построение трендовых моделей
- •4.4.3. Сглаживание временных рядов
- •4.4.4. Моделирование тенденции временного ряда при наличии структурных изменений
- •4.4.5. Влияние автокорреляции на структуру временного ряда
- •4.5. Многомерные временные ряды
- •4.5.1. Сущность и особенности многомерных динамических рядов
- •4.5.2. Способы построения множественной регрессионной модели по временным рядам
- •5.1.2. Связь однородности статистической совокупности с типом моделей
- •5.2. Динамическое моделирование взаимосвязей в структурно-однородных совокупностях
- •5.2.1. Методы построения пространственно-динамических
- •Моделей
- •5.2.2. Выбор вида пространственно-динамической модели
- •5.2.3. Динамизация параметров связи
- •5.3.2. Построение динамических моделей на основе временных выборок
- •6. Системы эконометрических уравнений
- •6.1.Общие понятия и способы представления систем эконометрических уравнений
- •6.2. Структурная и приведенная формы модели
- •6.3. Проблемы идентификации структурной модели
- •6.4. Оценка параметров структурной модели
- •6.5. Двухшаговый метод наименьших квадратов
- •7. Динамические эконометрические модели
- •7.1. Общая характеристика моделей с распределенным лагом и моделей авторегрессии
- •7.2. Оценка параметров авторегрессионных моделей
- •7.3. Интерпретация параметров модели с распределенным лагом
- •7.4. Интерпретация параметров модели авторегрессии
- •7.5. Изучение структуры лага и выбор вида модели с распределенным лагом
- •7.6. Лаги Алмон
- •8. Статистическое прогнозирование динамических рядов
- •8.1. Сущность и виды статистических прогнозов
- •8.2. Методы статистического прогнозирования
- •8.2.1. Экстраполяция динамических рядов
- •8.2.2. Прогнозирование на основе экспоненциального сглаживания
- •8.2.3. Прогнозирование на основе регрессионных и авторегрессионных моделей
- •Список литературы
4.3. Состав динамического ряда
Динамический ряд
не является однородным. Его составляющие
анализируются и моделируются различными
математическими способами. Каждый
уровень
![]() динамического ряда формируют следующие
элементы.
динамического ряда формируют следующие
элементы.
1. Основная тенденция
(тренд
![]() )
складывается под воздействием длительно
действующих факторов, определяющих
специфику данного процесса, поэтому
называется также вековой составляющей.
)
складывается под воздействием длительно
действующих факторов, определяющих
специфику данного процесса, поэтому
называется также вековой составляющей.
2. Случайная
составляющая
![]() отражает влияние различных факторов
стохастического характера, поэтому
искажает
.
отражает влияние различных факторов
стохастического характера, поэтому
искажает
.
Любой динамический ряд, как минимум, содержит эти две составляющие.
3. Сезонные
(квартальные) колебания
![]() .
.
4. Периодические колебания: продолжительность цикла колебаний не равна 1 кварталу.
Если указанные
элементы динамического ряда находятся
в аддитивной связи, то говорят об
аддитивном
ряде вида
![]() ,
если в мультипликативной, то – о
мультипликативном
динамическом ряде,
который может быть представлен как
,
если в мультипликативной, то – о
мультипликативном
динамическом ряде,
который может быть представлен как
![]() .
.
Для аддитивного ряда характерны примерно одинаковые отклонения от тренда за весь исследуемый период времени, а для мультипликативного амплитуда таких колебаний либо увеличивается, либо уменьшается с течением времени.
4.4. Моделирование одномерных динамических рядов
4.4.1. Типы экономического развития и их трендовые модели
Траектории, как математические модели экономического развития, классифицируются в зависимости от динамики цепного абсолютного прироста (формулы (4.1) и (4.4)).
Первому типу
экономического развития
соответствуют траектории с постоянной
скоростью (с константным или приблизительно
постоянным ростом). Данный тип развития
может аппроксимироваться следующими
моделями (без учета
![]() ):
):
 –
линейной;
–
линейной;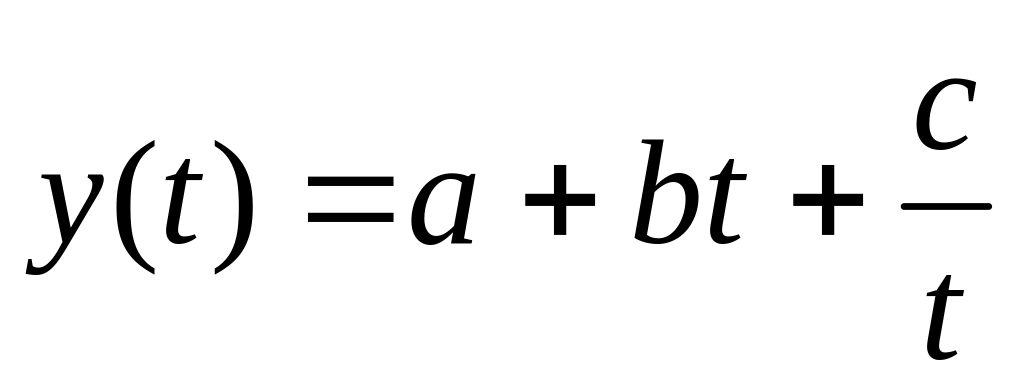 –
линейно-гиперболической;
–
линейно-гиперболической; 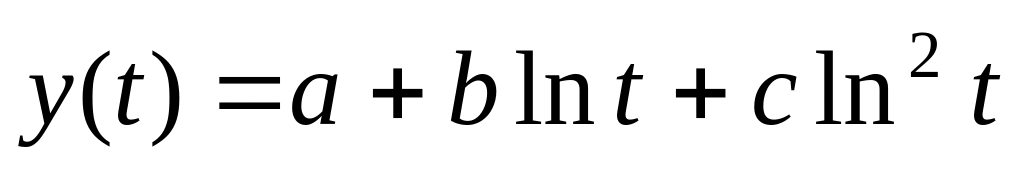 –
линейно-логарифмической
второго порядка.
–
линейно-логарифмической
второго порядка.
Второй вид развития может моделироваться траекториями с увеличивающейся скоростью, в частности,
 –
параболической
(при
–
параболической
(при
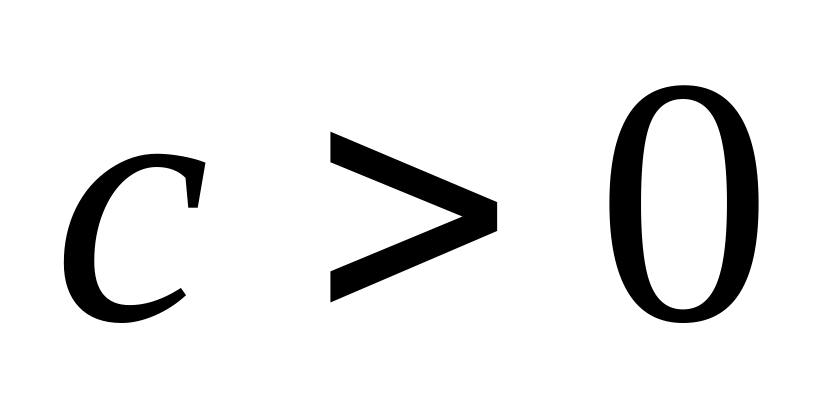 );
); –
параболой третьего
порядка (при
–
параболой третьего
порядка (при
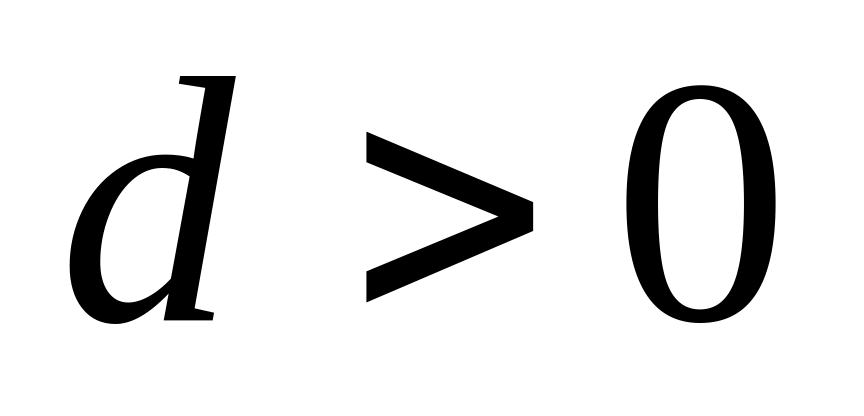 );
);
 –
степенной;
–
степенной;
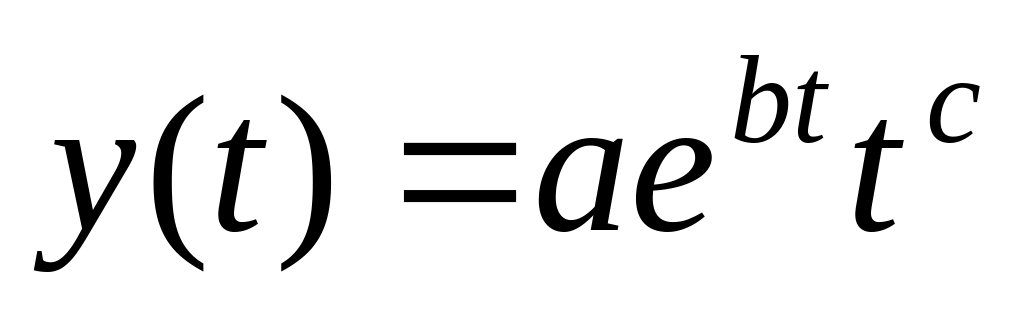 –
кинетической.
–
кинетической.
Третий тип развития – это изменение с уменьшающимся ростом. Выделяют следующие подгруппы моделей данного класса:
уменьшающийся рост, не имеющий предела:
a)
![]() –
линейно-логарифмическая;
–
линейно-логарифмическая;
b)
![]() ;
;
c)
![]() ;
;
уменьшающийся рост, имеющий предел:
d)
![]() –
гипербола первого порядка;
–
гипербола первого порядка;
e)
![]() –
гипербола второго порядка.
–
гипербола второго порядка.
Особый класс
представляют собой модели экономического
развития с качественным изменением
характеристик.
Их особенностью является наличие точки
перегиба
![]() ,
в которой скорость меняет свой знак,
проходя через нулевое значение абсолютного
ускорения (формула (4.6)),
,
в которой скорость меняет свой знак,
проходя через нулевое значение абсолютного
ускорения (формула (4.6)),
![]() .
.
Примеры функций данного типа:
линейно-логарифмическая второго порядка (при
 ),
для которой
),
для которой
![]() ;
;
парабола третьего порядка (при
 )
с точкой перегиба
)
с точкой перегиба
![]() .
.
Следует указать, что возможна не только кусочная аппроксимация развития на различных участках времени t, но и моделирование всего интервала времени одной функцией (п. 4.4.4).
4.4.2. Построение трендовых моделей
Методика построения трендовых моделей представляет собой сочетание качественного экономического анализа с формализованными математическими процедурами и реализуется в следующей последовательности.
1. Выбор класса (вида) уравнения тренда исходя из особенностей динамики исследуемого процесса (раздел 4.4.1.).
2. Расчет формальных
критериев качества аппроксимации,
отражающих степень соответствия модели
тренда исходному ряду, а именно, чем
меньше значение критерия, тем точнее
уравнение (по которому рассчитываются
теоретические значения
![]() )
моделирует эмпирические данные
)
моделирует эмпирические данные
![]() :
:
средней квадратичной ошибки аппроксимации (по аналогии с остаточной дисперсией – формула (1.10))
![]() ,
,
где n – длина динамического ряда;
k – количество оцениваемых параметров уравнения тренда;
относительной (линейной) ошибки аппроксимации
![]() .
.
Статистический анализ случайной компоненты , которая должна удовлетворять ряду формальных требований (п. 4.4.5).
Моделирование сезонных и циклических колебаний в случае установления факта их наличия (п. 4.4.5).
Окончательный выбор функции тренда с учетом формальных критериев и характера решаемых задач. Если решаются ретроспективные задачи, то уравнение тренда должно иметь наилучшие значения критериев для всего динамического ряда, если же – перспективные задачи, то предпочтение отдается функции, имеющей минимальные значения ошибок аппроксимации
 и
на последнем (в пределах ретроспективы)
интервале оси времени.
и
на последнем (в пределах ретроспективы)
интервале оси времени.
