Апериодическое движение

Рассмотрим уравнение (3.1), когда > .

Корни характеристического уравнения

действительные и меньше нуля.

Решение уравнения

. (3.7)

Так как < и < , то, независимо от значений и , при . Это означает, что с течением времени точка неограниченно приближается к равновесному положению.

Написав корни характеристического уравнения в виде , , получим

. (3.8)

Определим моменты, когда точка занимает крайние положения (в них ее скорость равна нулю)

.

Обозначим , тогда

,

или .

Получено неполное квадратное уравнение. Для момента времени имеем действительное и положительное значение только при > , которых в зависимости от и имеется или одно, или совсем не имеется, что относится и к случаю .

Н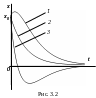 а рис. 3.2 показаны кривые возможных движений точки в зависимости от начальных условий при > .

Кривая 1 соответствует начальной скорости, направленной в положительную сторону оси .

Кривая 2 – относительно небольшой начальной скорости, направленной в отрицательную сторону оси .

Кривая 3 - большой начальной скорости, направленной в отрицательную сторону оси .

При корни характеристического уравнения равны между собой ( ), и решение дифференциального уравнения выглядит

. (3.9)

Характер движения тот же, что и при > . В случае большого сопротивления ( >> ) колебаний нет. Это движение называется апериодическим затухающим.

Вынужденные колебания без учета сопротивления

На МТ массой , кроме силы тяжести и восстанавливающей силы , действует периодически изменяющаяся сила (Н – ее амплитуда, р – частота, - начальная фаза), называемая возмущающей силой (рис. 2.8-д). Тогда дифференциальное уравнение движения МТ

, (3.10)

или .

Обозначив , (частота собственных колебаний), имеем

. (3.11)

Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, неоднородное. Его общее решение есть сумма общего решения однородного и частного решения неоднородного уравнений

. (3.12)

Решением однородного уравнения является

, или . (3.13)

Частное решение неоднородного уравнения имеет разные выражения в зависимости от р.

Рассмотрим случай . Решение ищем в виде

, (3.14)

где требуется найти.

Находим производные , и подставляем в (3.11)

+ ,

откуда , и частное решение имеет вид

. (3.15)

Тогда общее решение

, (3.16)

или .

Произвольные постоянные интегрирования ( ) находятся с помощью начальных условий.

Амплитуда вынужденных колебаний

. (3.17)

При > , то есть вынужденные колебания и возмущающая сила находятся в одной фазе (имеют одновременно максимумы и минимумы).

При > вынужденные колебания и возмущающая сила имеют противоположные фазы

. (3.18)