Главный вектор и главный момент сил инерции

Как всякая система сил, система сил инерции может быть приведена к какому-либо центру О.

Рассмотрим совокупность сил инерции .

Главный вектор системы сил инерции

.

Заменим , тогда

,

где (M – масса системы).

Тогда

или

, (11.8)

т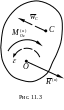 о есть главный вектор сил инерции для системы МТ равен силе инерции центра масс системы в предположении, что в нем сосредоточена вся масса системы (рис.11.3).

Главный момент сил инерции

.

С другой стороны, на основании теоремы об изменении кинетического момента системы имеем

.

Таким образом,

, (11.9)

то есть главный момент сил инерции относительно центра О равен взятому с обратным знаком вектору, выражающему производную по времени от кинетического момента системы относительно того же центра.

Аналогично для проекций. Например,

. (11.10)

В частности, при вращении твердого тела вокруг оси z его кинетический момент . Следовательно, для тела, вращающегося вокруг неподвижной оси, можно написать

,

то есть

. (11.11)

Этот момент создают касательные силы инерции.

Частные случаи

Поступательное движение. Ускорения всех точек тела одинаковы и равны ускорению центра масс С. Силы инерции точек образуют систему параллельных сил и имеют равнодействующую, проходящую через центр масс

,

то есть при поступательном движении силы инерции твердого тела приводятся к равнодействующей , проходящей через центр масс.

Вращательное движение.

Положим, тело вращается вокруг оси , перпендикулярной к плоскости чертежа (рис. 11.3), с которой совпадает плоскость материальной симметрии тела. Приводя силы инерции к центру О, получим результирующую силу и пару, лежащие в плоскости симметрии. Тогда, с учетом (11.11), имеем

, (11.12)

то есть система сил инерции вращающего тела приводится к силе , проходящей чрез центр О, и паре с моментом , лежащей в плоскости симметрии тела.

Вращение вокруг неподвижной оси, проходящей через центр масс тела.

В этом случае , поэтому . Поэтому система сил инерции приводится к паре сил с моментом , лежащей в плоскости симметрии тела.

Плоскопараллельное движение.

П оложим, тело имеет плоскость симметрии и движется параллельно ей. В этом случае система сил инерции приводится к лежащим в плоскости симметрии силе инерции , приложенной в центре масс, и паре сил с моментом .

Рассмотрим тело, вращающееся вокруг неподвижной оси z с постоянной угловой скоростью (рис. 11.4).

Обозначим проекции на координатные оси главного вектора внешних сил , главного вектора сил инерции , главного момента внешних сил , главного момента сил инерции , динамические реакции . Напишем уравнения динамического равновесия тела

,

,

, (11.13)

,

,

.

Последнее уравнение удовлетворяется тождественно, так как при отсутствии углового ускорения каждый из его членов сам по себе равен нулю.

Главный вектор сил инерции при равен произведению массы тела на нормальное ускорение центра масс С тела

, (11.14)

где m – масса тела, нормальное ускорение точки С .

Тогда

, , .

Для определения проекций возьмем точку тела с массой , отстоящую от оси на расстоянии , центробежная сила инерции которой , проекции которой по аналогии с равны , , . Следовательно, моменты относительно осей

, .(11.15)

Суммируя эти выражения для всех точек тела, находим

, , (11.16)

где - центробежные моменты инерции тела.

Подставляем найденные значения в (11.13)

,

,

, (11.17)

,

.

Из этих уравнений находятся динамические реакции при равномерном вращении тела вокруг оси z. Статические реакции определяются из уравнений (11.17), если принять в них .

Из этих уравнений следует, что вращение не будет влиять на значения реакций в подшипниках A и B, если что является признаком динамической уравновешенности тела при вращении вокруг оси z.