Лекция 13
Обобщенная сила. Условия равновесия в обобщенных координатах.
Общее уравнение динамики (уравнение Даламбера-Лагранжа)
Условия равновесия в обобщенных координатах
Обобщенной
силой
,
соответствующей обобщенной координате
,
называется скалярная величина,
определяемая отношением элементарной
работы действующих сил на перемещении
системы, вызванном элементарным
приращением
координаты
,
к величине этого приращения
.
(13.1)
Пусть механическая система состоит из N материальных точек с голономными связями, имеющих n степеней свободы (то есть n обобщенных координат q).
По принципу возможных перемещений имеем
.
(13.2)
Через обобщенные силы это выражение имеет вид
,
или
.
(13.3)
Так как все
приращения независимы, то множители
можно записывать произвольно.
Примем
.
Тогда на основании (13.3)
,
откуда
.
Затем примем
,
тогда
,
следовательно,
и т. д.
Таким образом, получены условия равновесия в обобщенных координатах
,
,…,
.
(13.4)
Для равновесия голономной системы с n степенями свободы в ее положении, характеризуемом обобщенными координатами q1, q2, …, qn , необходимо и достаточно, чтобы значения всех обобщенных сил, соответствующие значениям обобщенных координат, равнялись нулю.
Общее уравнение динамики
Пусть имеется система, состоящая из N материальных точек, имеющих произвольные двусторонние, неосвобождающие связи.
Тогда на основании принципа Даламбера для к-той точки можно написать
=0,
(13.5)
где
- векторы равнодействующих, соответственно,
активных, реактивных и инерционных сил,
действующих на точку.
Таким образом, точка находится в состоянии динамического равновесия, которое можно выразить принципом возможных перемещений. В результате принцип Даламбера объединяется с принципом возможных перемещений Лагранжа применительно к движущейся системе и образует общее уравнение динамики: сумма элементарных работ всех непосредственно приложенных к точкам системы активных, реактивных сил и сил инерции равна нулю на любом возможном перемещении системы из положения, занимаемого ею в текущий момент времени.
Оно имеет выражение
.
(13.6)
При этом связи могут быть реономными ввиду равновесия системы.
Общее уравнение
динамики можно представить в иной форме,
используя выражения
,
,
или
,
(13.7)
Можно получить это уравнение в аналитической форме, использовав известные соотношения
,
,
,
,
.
Тогда на основании (13.7) имеем
(13.8)
В случае идеальных связей сумма элементарных работ их реакций тождественно равна нулю на любом возможном перемещении системы из положения, занимаемого в процессе движения,
.
(13.9)
Уравнения приобретают вид
,
,
(13.10)
Пример.
Механическая система состоит из
ступенчатых дисков 1 и
2, тел 3, 4, 5, 6 и невесомого блока (рис.
13.1-а). Известно: силы тяжести
,
момент
;
радиусы
;
радиусы инерции дисков
.
Коэффициент трения
,
коэффициент сопротивления качению
.
Определить ускорение центра колеса 4.
Р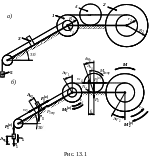
ешение.
Составим расчетную схему.
Выполним в масштабе чертеж. Покажем на нем:
- силы тяжести тел 3,4, 5, 6;
- линейные и угловые ускорения,
- инерционные силовые факторы, направленные противоположно ускорениям (рис. 13.1-б).
Сообщим системе
возможное перемещение. Только теперь
можно показать на чертеже силу трения
и момент сопротивления качению
,
направленные противоположно перемещениям
тел.
Напишем общее уравнение динамики
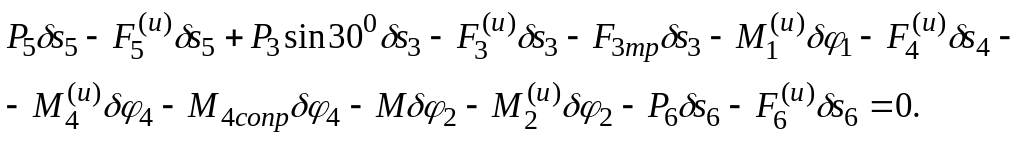(13.11)
Установим связь между возможными перемещениями. Удобно перемещения тел выражать через перемещение того тела, ускорение которого нужно найти по условию.
,
Соотношения между ускорениями (они аналогичны соотношениям между перемещениями)
,
,
,
.
Силовые инерционные факторы
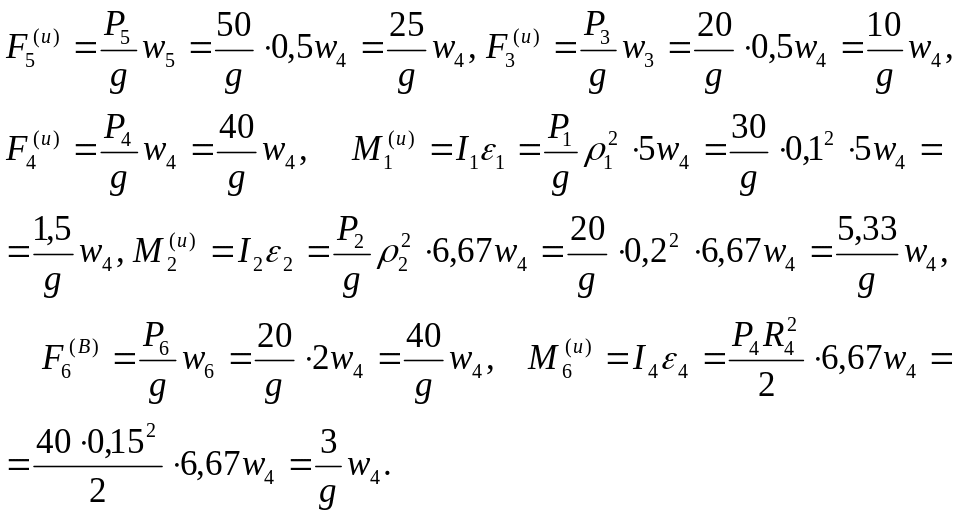
Сила трения
момент сопротивления качению колеса 4 (N4=P4)
.
Найденные значения подставляем в исходное выражение (13.11)
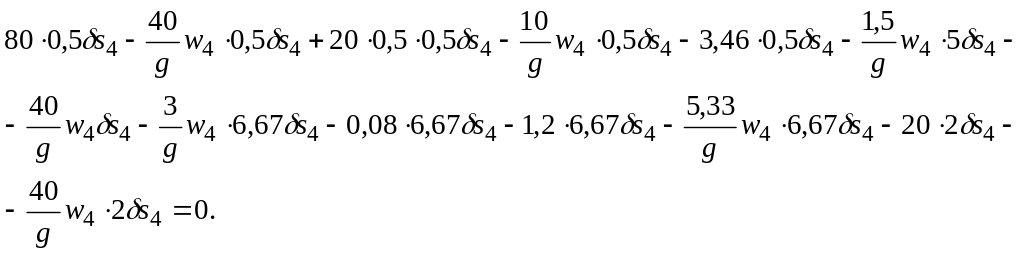
После приведения подобных получим
,
откуда находим искомое ускорение тела 4
.