Моменты инерции

П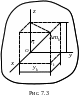 ри решении ряда задач динамики системы определяются динамические величины, выражающиеся через суммы произведений масс точек системы на квадраты их расстояний до оси, точки или плоскости. Эти величины характеризуют распределение масс системы относительно оси, точки или плоскости. Они называются моментами инерции, соответственно, относительно оси, точки, плоскости.

Разобьем твердое тело на n элементарных частиц и напишем выражения его моментов инерции (рис. 7.3).

Относительно полюса О

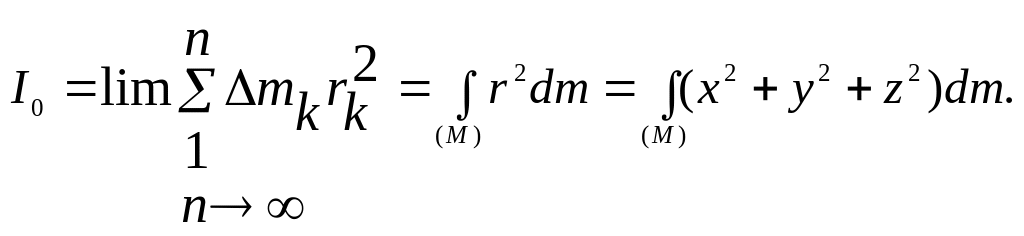(7.9)

Относительно осей

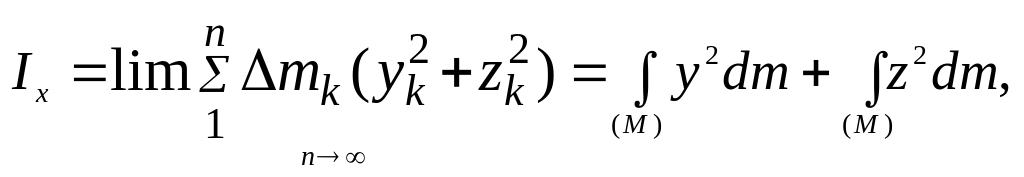
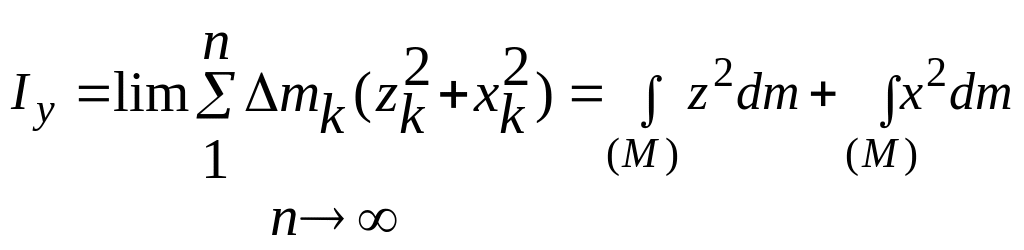, (7.10)

.

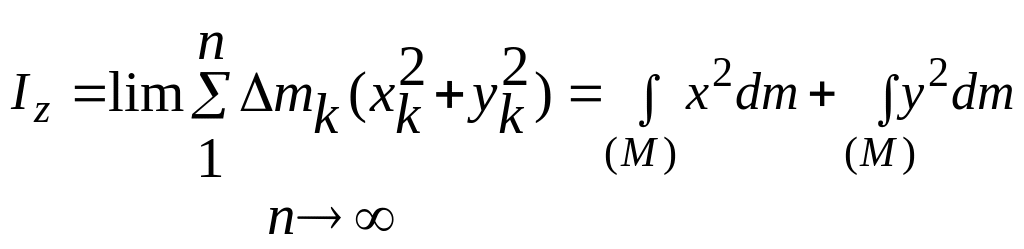Относительно плоскостей

,

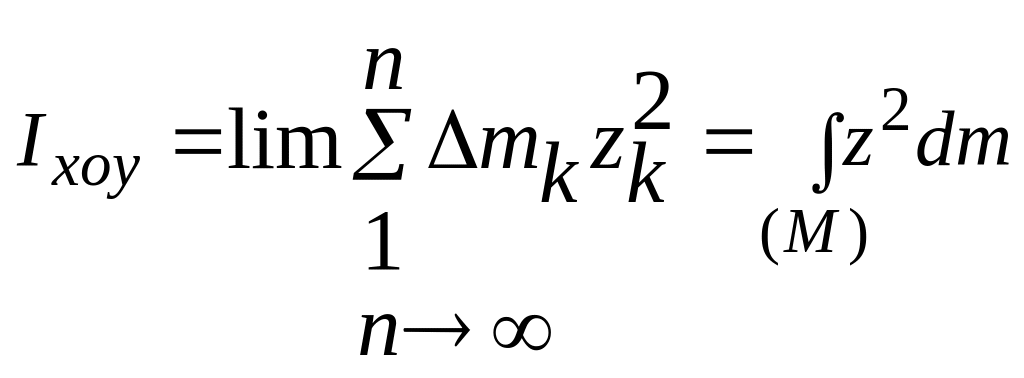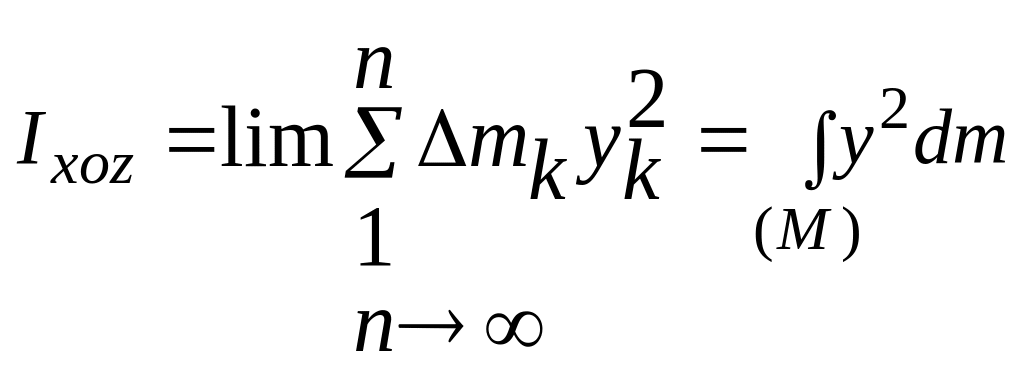, (7.11)

.

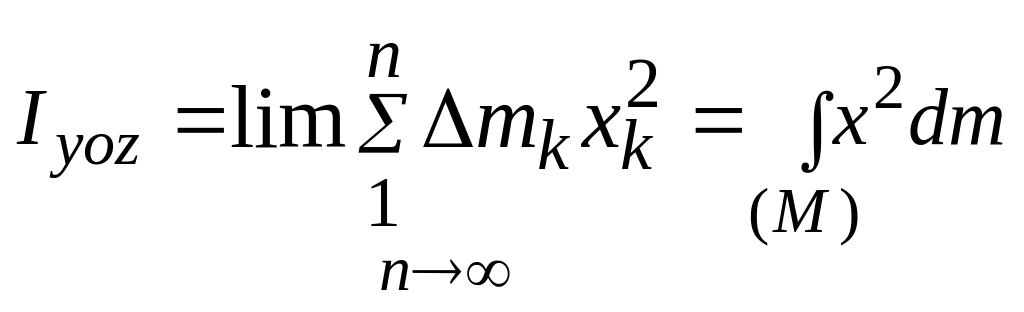Отсюда вытекают соотношения

, (7.12)

то есть сумма моментов инерции относительно координатных осей равна двум моментам инерции относительно полюса (начала системы координат);

, (7.13)

то есть сумма моментов инерции относительно координатных плоскостей равна моменту инерции относительно полюса.

Размерность момента инерции [I]=[ ]. В системе СИ .

Нередко при расчетах используется понятие радиуса инерции. Радиусом инерции относительно оси называется линейная величина, определяемая из соотношения

, откуда , (7.14)

где - масса тела.

Радиус инерции равен расстоянию от оси той точки, в которой надо сосредоточить массу тела, чтобы ее момент инерции относительно этой оси был равен моменту инерции тела.

Понятием радиуса инерции пользуются, когда имеется тело неправильной (сложной) формы. Тогда в техническую документацию на изделие вносится масса и радиус инерции, соответствующие значению момента инерции, найденному экспериментально.

Теорема Штейнера-Гюйгенса

Т еорема: момент инерции системы относительно какой-либо оси равен моменту инерции системы относительно оси, проходящей через центр масс системы параллельно ей, плюс произведение массы системы на квадрат расстояния между осями (рис. 7.4).

Напишем

,

,

где по теореме косинусов .

Тогда

,

где , , .

Следовательно,

. (7.15)

Из этой формулы видно, что для совокупности параллельных осей, момент инерции относительно центральной оси (проходящий через центр масс) является наименьшим.

М оменты инерции однородных тел

Стержень (рис. 7.5). Масса М, длина .

Относительно оси, проходящей через конец стержня,

, (7.16)

где - погонная масса стержня.

Ц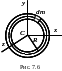 ентральный момент инерции находим по теореме Штейнера-Гюйгенса

, откуда . (7.17)

Кольцо (рис. 7.6).

Масса распределена по ободу.

Центральный момент инерции относительно оси z, перпендикулярной к плоскости кольца

. (7.18)

В соответствии с (7.12)

. (7.19)

Круглый диск (рис. 7.7).

Центральный момент инерции относительно оси z, перпендикулярной к плоскости диска

,

где (V- объем диска).

Тогда

. (7.20)

На основании (7.12) другие осевые моменты инерции

. (7.21)

Шар (рис. 7.8).

Момент инерции относительно центра

, где ,

тогда ,

где плотность ,

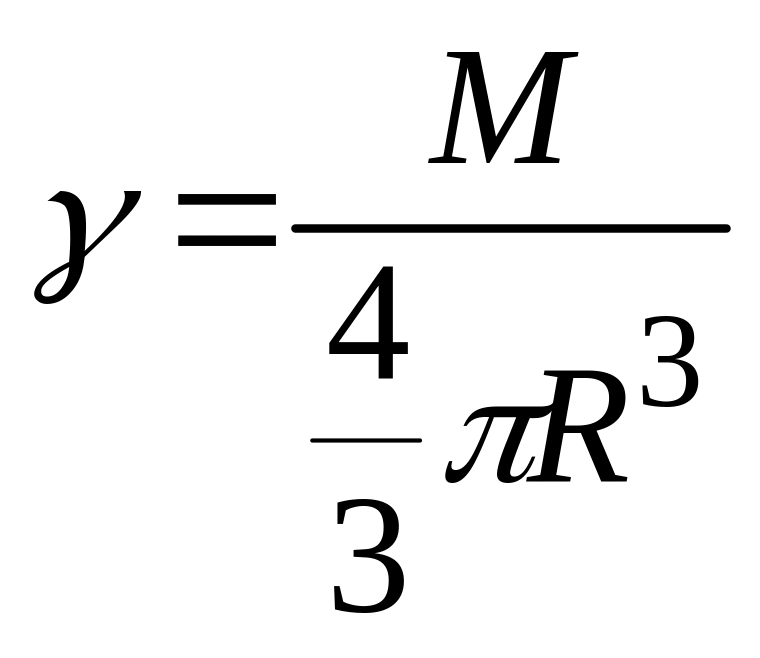тогда 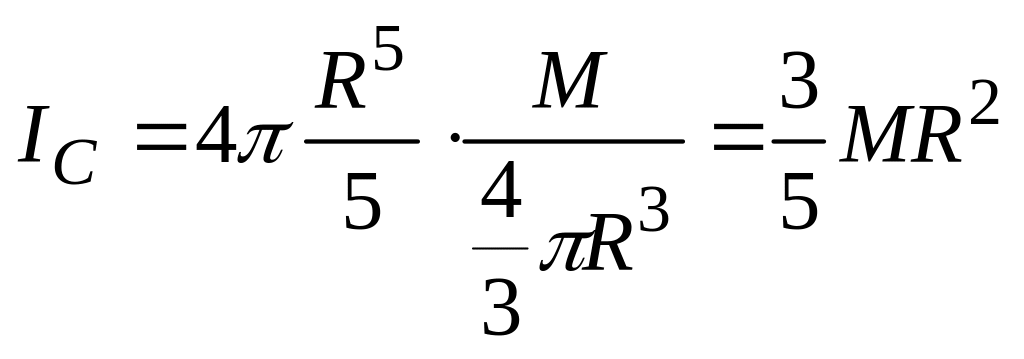. (7.22)

На основании (7.13) осевые моменты инерции

. (7.23)