Возможное (виртуальное) перемещение

Возможным (виртуальным) перемещением точки называется бесконечно малое ее перемещение, допускаемое в данный момент наложенными на нее связями.

Это перемещение не следует смешивать с действительным, которое обусловлено действующими на МТ силами, а возможное – наложенными связями. Оно может являться частным случаем возможного перемещения.

Возможное перемещение, в отличие от действительного перемещения , обозначается .

Поскольку возможные перемещения точек являются бесконечно малыми, то элементы криволинейного перемещения могут быть заменены элементами прямолинейных перемещений.

Возможным перемещением системы называется такое ее перемещение, которое определяется совокупностью возможных перемещений ее точек в данный момент.

Возможное перемещение несвободной системы ограничено наложенными на нее связями, и поэтому для определения ее положения необязательно знать координаты всех ее точек.

Д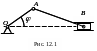 ля кривошипно-шатунного механизма (рис. 12.1) достаточно знать угол φ поворота кривошипа, и тогда координаты всех точек этого механизма могут быть выражены функцией одной независимой переменной – угла φ. Такая система называется системой с одной степенью свободы.

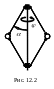
Для определения положения центробежного регулятора в пространстве необходимо знать углы φ и α (рис. 12.2). Эта система имеет две степени свободы.

Независимые координаты, заданием которых определяется положение всех точек данной системы, называются обобщенными координатами. Число обобщенных координат равно числу степеней свободы. Если положение точек системы определяется заданием n независимых величин (обобщенных координат), то такая система имеет n степеней свободы, то есть число независимых возможных перемещений системы определяет число ее степеней свободы.

Идеальные связи

Идеальными связями, или связями без трения, называются такие связи, при которых сумма элементарных работ их реакций равна нулю на любом возможном перемещении системы. К их числу относятся все стационарные голономные связи без трения.

Для к-той точки введем обозначения сил: – равнодействующая активных сил, - равнодействующая реакций связей, - равнодействующая всех сил.

Тогда

. (12.4)

Придадим какое-либо возможное перемещение системе, то есть совокупность перемещений всех ее точек . Найдем работу сил, действующих на этом перемещение

. (12.5)

Если , то связь идеальна, и в этом случае .

Принцип возможных (виртуальных) перемещений

Пусть имеется система несвободных МТ, находящаяся в равновесии.

Выделим материальную точку М_к. Обозначим: – равнодействующая активных сил, - равнодействующая реакций связей.

Т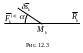 ак как система находится в равновесии, то (рис. 12.3).

Сообщим системе возможное перемещение, тогда точка М_к получит элементарное перемещение . Сумма элементарных работ на возможном перемещении

.

Написав такие равенства для всех точек и просуммировав их почленно, получим

. (12.6)

Для идеальных связей , следовательно,

. (12.7)

Нетрудно доказать и обратное: если , то система находится в равновесии.

Принцип возможных (виртуальных) перемещений формулируется: для равновесия системы с идеальными связями необходимо и достаточно, чтобы равнялась нулю сумма элементарных работ всех приложенных к ней активных (внешних) сил на любом возможном перемещении системы из положения равновесия.

Выражая работу сил через проекции, имеем

, (12.8)

где - проекции приложенных к системе активных сил, - элементарные приращения координат (их вариации) к-той точки системы на ее возможном перемещении.

Этот принцип применим и тогда, когда имеются связи с трением. Тогда силу трения следует считать активной.

Принцип возможных перемещений применяется в случаях, когда требуется найти неизвестные силовые факторы для статически уравновешенных систем. Он также применим для определения опорных реакций.

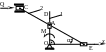
Пример. В кулисном механизме, расположенном в горизонтальной плоскости, ползуны А и В могут перемещаться вдоль стержней OD и OE кривошипа 1, жестко соединенных между собой под прямым углом (рис. 12.4-а). Стержень 2 шарнирно связан с ползунами А,В,С. Ползун С движется по направляющим параллельно оси х.

Пренебрегая трением, определить силу Q, уравновешивающую момент М. Дано: AB=AC= , ABO= , М.

Решение.

а)

Дадим системе возможное перемещение (рис. 12.4-б). На основании принципа возможных перемещений

б)

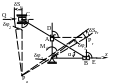
, где , .

Установим связь между возможными перемещениями.

Мгновенный центр вращения тела 2 в движении относительно кривошипа 1 находится в точке , а в абсолютном движении – в точке .

Из рисунка видно:

Рис. 12.4

, .

Следовательно, .

Тогда , откуда .