Теорема об изменении кинетического момента системы

Теорема: изменение кинетического момента системы относительно какой-либо точки за время удара равно векторной сумме моментов внешних ударных импульсов, приложенных к системе, относительно той же точки.

Применим теорему об изменении кинетического момента системы

,

где - кинетический момент системы относительно неподвижной точки , - главный момент внешних сил, действующих на систему.

Тогда

.

Интегрируем это выражение в пределах от 0 до

.

Левая часть представляет собой изменение кинетического момента системы за время удара . Преобразуем правую часть

= ,

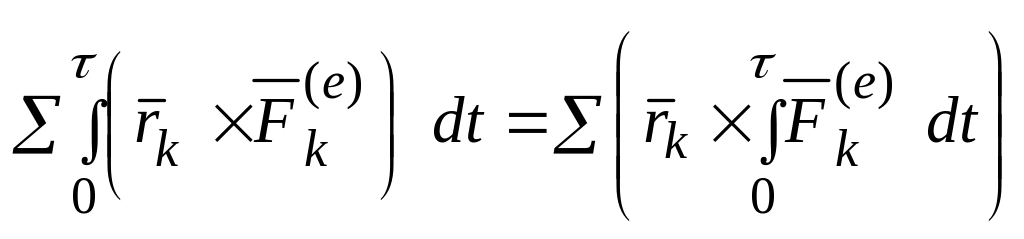где перемещениям и во время удара пренебрегаем, то есть .

Так как - внешний ударный импульс, то

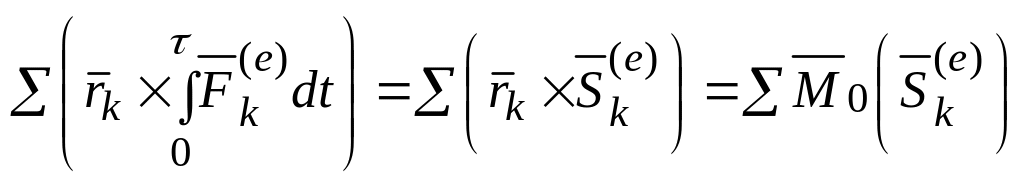. (17.7)

Окончательно имеем

. (17.8)

Соотношение (17.8) справедливо и в проекциях на любую ось, например,

,

то есть изменение кинетического момента относительно какой-либо оси за время удара равно алгебраической сумме моментов внешних ударных импульсов относительно той же оси.

Следствие. При , то есть, если сумма моментов внешних ударных импульсов, приложенных к системе, относительно какой-либо точки равна нулю, то кинетический момент системы относительно этой точки при ударе не изменяется.

Это справедливо также по отношению к любой оси.

Действие ударных сил на тело, вращающееся вокруг неподвижной оси. Центр удара

Если произвести удар с ударным импульсом по телу, имеющему ось вращения, то можно установить условия, при выполнении которых н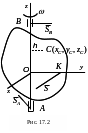 е возникает ударных реакций в подшипниках, расположенных на оси вращения.

Допустим, тело до удара вращалось вокруг неподвижной оси с угловой скоростью (рис. 17.2).

Положим, к телу приложили ударный импульс , и оно стало вращаться с угловой скоростью .

Освободим тело от связей и заменим их импульсными реакциями и , применив к явлению удара теоремы об изменении количества движения и кинетического момента системы

, (17.9)

,

где и - векторы количества движения и кинетического момента системы.

По формуле Эйлера скорость точки

.

Тогда , где - масса тела, - радиус-вектор центра масс тела.

Так как и направлены по оси вращения, то

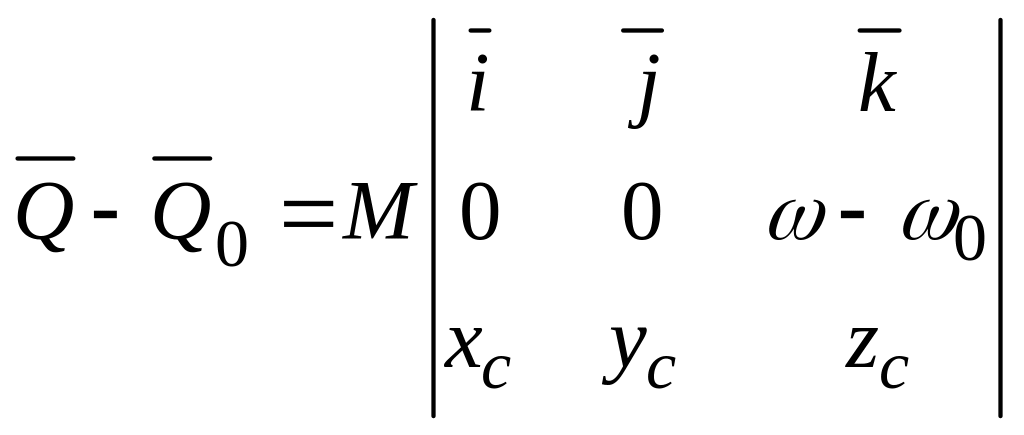. (17.10)

Проекции кинетического момента на оси координат находим по формулам для тела, имеющего одну закреплённую точку, при условии ,

,

,

.

Следовательно,

,

, (17.11)

.

Проектируем (17.9) на оси координат с учетом (17.10) и (17.11)

,

,

,

, (17.12)

,

.

Из системы (17.12) находятся импульсы и и изменение угловой скорости для заданного импульса .

Найдём условия, при которых . Из (17.12) в этом случае имеем

,

,

,

, (17.13)

,

.

Из (17.13) очевидно, что если , то ударный импульс параллелен плоскости . Выберем начало координат О так, чтобы этот вектор лежал в самой плоскости , а ось направим параллельно вектору . Тогда вектор пересечёт ось в точке K. При таком выборе координат моментных осей , , , .

Поэтому из (17.13) из второго уравнения , из четвёртого , из пятого , то есть центр масс находится в плоскости и ось вращения является главной осью инерции.

Так как вектор параллелен оси , то, следовательно, он перпендикулярен плоскости , проходящей через ось вращения и центр масс.

Обозначим , тогда (при > ).

Исключая , находим

. (17.14)

При выбранной системе координат - расстояние от центра масс до оси вращения. Назовём его , тогда . Получена формула для вычисления приведённой длины физического маятника.

Точка пересечения линии действия ударного импульса с плоскостью, проходящей через ось вращения и центр масс, при отсутствии ударных реакций в подшипниках, называется центром удара.

Любой ударный импульс , линия действия которого проходит через точку К перпендикулярно к плоскости, соединяющей ось вращения и центр масс, не вызывает ударных реакций в подшипниках, если ось вращения является главной осью инерции для точки О (точки пересечения оси вращения с перпендикулярной плоскостью, содержащей ударный импульс ). Расстояние от оси вращения до линии ударного импульса равно приведённой длине физического маятника. Центр удара К и центр масс C лежат по одну сторону от оси вращения.

Если центр масс лежит на оси вращения , то центр удара находится в бесконечности. Тогда по формуле (17.10), то есть , откуда . Ударный импульс, приложенный к телу, полностью передается на подшипники.