Лекция 8

Работа внутренних сил. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси. Кинетическая энергия системы. Вычисление кинетической энергии твердого тела в различных случаях его движения. Теорема об изменении кинетической энергии системы

Работа внутренних сил

Р ассмотрим работу внутренних сил в абсолютно твердом теле (рис. 8.1). Пусть точки А и В при движении тела получают перемещения и . Силы – силы взаимодействия между точками.

Разложим перемещения точек по направлениям, параллельному и перпендикулярному прямой АВ

, . (8.1)

Заметим, что силы и на перемещениях и , перпендикулярных к их векторам, работы не совершают. С другой стороны, поскольку , то , то есть эти перемещения равны по модулю и одинаково направлены. Следовательно,

. (8.2)

Этот вывод можно отнести к любой паре точек системы. Таким образом, сумма работ внутренних сил неизменяемой системы при любом её перемещении равна нулю.

Отметим, что это справедливо только для случая неизменяемой системы, а для произвольной механической системы в общем случае работа внутренних сил отличается от нуля.

Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси

Скорость точки М по векторной формуле Эйлера (рис. 8.2)

.

Элементарная работа силы

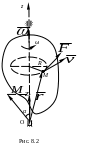
. (8.3)

В смешанном векторном произведении сомножители можно переставлять в круговом порядке

. (8.4)

Следовательно,

,

где – векторный момент силы относительно точки О.

Учитывая, что , а , окончательно имеем

. (8.5)

Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на дифференциал угла поворота.

Полная работа

.(8.1)

Если , то , где – угол поворота тела, на котором вычисляется работа силы.

Так как , то мощность

, (8.6)

то есть мощность силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению момента силы относительно этой оси на угловую скорость.

Если сила направлена по касательной к окружности, описываемой точкой её приложения, то она называется окружной силой. Ее момент в этом случае .

Кинетическая энергия механической системы

Кинетической энергией механической системы Т называется сумма кинетических энергий всех МТ механической системы

. (8.7)

Кинетическая энергия механической системы, как и кинетическая энергия МТ, не зависит от направления скоростей точек. Она равна нулю только в том случае, когда все точки находятся в покое.

Вычисление кинетической энергии твердого тела в различных случаях его движения

Поступательное движение тела. Скорости всех его точек равны между собой, следовательно,

,

где - масса тела,

тогда

, (8.8)

то есть кинетическая энергия поступательно движущегося тела равна половине произведения массы М на квадрат его скорости .

При поступательном движении тела она вычисляется так же, как и для одной точки, у которой масса равна массе всего тела. По этой формуле находится кинетическая энергия любой системы, движущейся так, что модули скоростей всех её точек одинаковы.

В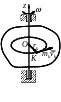 ращение тела вокруг неподвижной оси (рис. 8.3). Скорость любой точки определяется по формуле , где – кратчайшее расстояние от точки до оси вращения, – угловая скорость вращения тела. Тогда

так как угловая скорость для всех точек одинакова и может быть вынесена за знак суммы.

З

Рис. 8.3

десь – момент инерции относительно оси вращения, следовательно,

, (8.9)

то есть кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции точки относительно этой оси на квадрат его угловой скорости.

С равнивая формулы (8.1) и (8.2), отметим, что они аналогичны. Друг другу при поступательном и вращательном движении тела соответствуют скорости и , масса M и момент инерции I, играющий роль массы при вращении.

Плоско-параллельное движение тела (рис. 8.4).

Кинетическая энергия вычисляется в соответствии с теоремой Кёнига. Покажем сечение тела плоскостью, проходящее через центр масс С и параллельное данной неподвижной плоскости.

Пусть известны и . Тело в данное мгновение вращается вокруг МЦС, положение которого определяется отрезком СР, повернутым перпендикулярно к и направленным в сторону вращения ( ).

Кинетическая энергия тела

где – момент инерции тела относительно оси, перпендикулярной к плоскости сечения, проходящей через МЦС и являющейся мгновенной осью вращения.

Пользоваться этой формулой неудобно, так как . Преобразуем момент инерции по формуле Штейнера-Гюйгенса: , где – момент инерции тела относительно центральной оси, параллельной мгновенной оси вращения.

Тогда

.

Окончательно имеем

, (8.10)

то есть кинетическая энергия тела при плоско-параллельном движении равна сумме кинетических энергий тела в переносном поступательном движении со скоростью центра масс и вращательного движения вокруг центральной оси, перпендикулярной плоскости движения.

П ример. Вычислить кинетическую энергию гусеницы трактора, движущегося со скоростью . Расстояние между осями , радиус колеса r, погонный вес гусеничной цепи (рис. 8.5-а).

Разобьем тело гусеницы на участки I, II, III, IV (рис. 8.5-б). Тогда кинетическая энергия гусеницы

,

где (скорость участка I равна нулю). Участки II, III совокупно представляют собой кольцо, движущееся плоско-параллельно, его масса , момент инерции , скорость центра масс , угловая скорость , поэтому

.

Участок IV движется поступательно со скоростью , его масса , поэтому .

Следовательно, кинетическая энергия гусеницы

.