Каждую из сил можно представить , а так как , то , откуда , то есть модули ускорений, сообщаемых друг другу материальными точками при взаимодействии, обратно пропорциональны их массам.

Четвертый закон (закон независимости действия сил).

Материальная точка под действием нескольких сил получает ускорение, равное геометрической сумме тех ускорений, которые она получает от каждой силы, действующей отдельно, независимо от других.

Иначе, система сил, приложенных к одной МТ, динамически эквивалентна одной равнодействующей силе, равной главному вектору системы сил.

Пусть на МТ массой действуют силы , сообщая ей ускорение . При этом каждая из сил сообщает 3ускорения . Ускорение при действии нескольких сил является вектороной суммой ускорений, созданнх отдельными силами, то есть

. (1.4)

Умножим обе части этого выражения на

, (1.5)

где , , …, .

Тогда

,

следовательно,

, (1.6)

где обозначено .

Получено основное уравнение динамики для случая одновременного действия нескольких сил. Под силой подразумевается равнодействующая всех сил, действующих на МТ.

Системы единиц

Все физические величины могут быть выражены через три основные единицы, совокупность которых определяет их систему: единицы длины, времени и массы (или силы в технической системе).

Техническая система единиц (использовалась до 1961 года).

Основные единицы: 1 метр ( ) – длина, 1 секунда ( ) – время, 1 килограмм ( ) – сила.

Единица массы - техническая единица массы (т.е.м.): . Это масса, которой сила сообщает ускорение . Т.е.м. - это масса тела, вес которого равен 9,81 .

Международная система единиц (СИ).

Принята в 1961 году в Париже XI-ой Генеральной конференцией по мерам и весам.

Основные единицы: 1 метр ( ) – длина, 1 секунда ( ) – время, 1 килограмм ( ) – масса.

Единица силы 1 (ньютон). Это сила, которая массе сообщает ускорение .

Единица работы (энергии) джоуль (дж): .

Имеют место соотношения: , или .

Система (известна из прошлого).

Основные единицы: 1 сантиметр (см) – длина, 1 секунда (с) – время, 1 грамм (г) – масса.

Единица силы дина. Это такая сила, которая массе 1 г сообщает ускорение : 1 .

Справедливо соотношение: , .

Единица работы (энергии): .

Дифференциальные уравнения движения материальной точки Пользуясь основным законом динамики, можно вывести дифференциальные уравнения движения мт в различных системах координат.

В декартовых координатах (рис. 1.2).

Обозначая через равнодействующую всех активных и реактивных сил, приложенных к точке, напишем

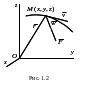
, (1.7)

где ускорение .

Дифференциальное уравнение движения МТ в векторной форме

. (1.8)

Спроектируем это уравнение на оси

, , , (1.9)

где , ,

.

Дифференциальные уравнения движения МТ в прямоугольной декартовой системе координат имеют вид

, , .

При движении точки в плоскости остаются два уравнения, в прямолинейном движении – одно.

В естественных координатах.

У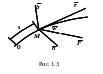 скорения вдоль осей координат: касательное , нормальное , бинормальное (рис.1.3).

Проектируя уравнение на координатные оси, получим дифференциальные уравнения движения МТ в естественных координатах

, , . (1.10)