Лекция 6

Элементарная работа силы. Работа силы на конечном пути. Мощность. Теорема о работе равнодействующей. Аналитическое выражение элементарной работы силы. Работа силы тяжести, силы упругости. Теорема об изменении кинетической энергии материальной точки

Работа силы

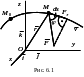
Работа силы на каком-либо перемещении является одной из основных характеристик, показывающих влияние силы на движение МТ. Элементарная работы силы F – это работа силы на бесконечно малом перемещении (рис. 6.1). Она определяется по формуле

, (6.1)

где – проекция силы на направление скорости точки (касательной к траектории).

Элементарная работа является скалярной величиной. Ее знак определяется знаком проекции силы , так как >0. При >0 dA>0, а при <0 dA<0. Так как =Fcosφ, где φ – угол между силой и направлением скорости , то выражение элементарной работы имеет вид

. (6.2)

В этой формуле F>0 и ds>0, и знак dA определяется знаком cosφ. Если φ<90⁰, то dA>0; если φ>90⁰, то dA<0.

Таким образом, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.

Отметим частные случаи:

если φ=0⁰, то dA=Fds,

если φ=90⁰, то dA=0 (работа силы на перпендикулярном к ней перемещении равна нулю),

если φ=180^0,, то dA=-Fds (работа силы отрицательна).

Следовательно, если сила перпендикулярна к элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной к скорости составляющей F_n всегда равна нулю.

Приведем другие формулы для определения элементарной работы силы.

Из кинематики известно: , , следовательно, .

Поэтому , то есть элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.

Так как , то

, (6.3)

то есть элементарная работа силы равна скалярному произведению ее элементарного импульса на скорость точки.

Если силу и радиус-вектор разложить по осям координат, то

, ,

откуда .

Следовательно,

. (6.4)

Эта формула называется аналитическим выражением элементарной работы силы.

Для определения полной работы силы на перемещении от точки М₀ до точки М разобьем это перемещение на перемещений, каждое из которых в пределе (при ) переходит в элементарное.

Тогда работа может быть выражена

,

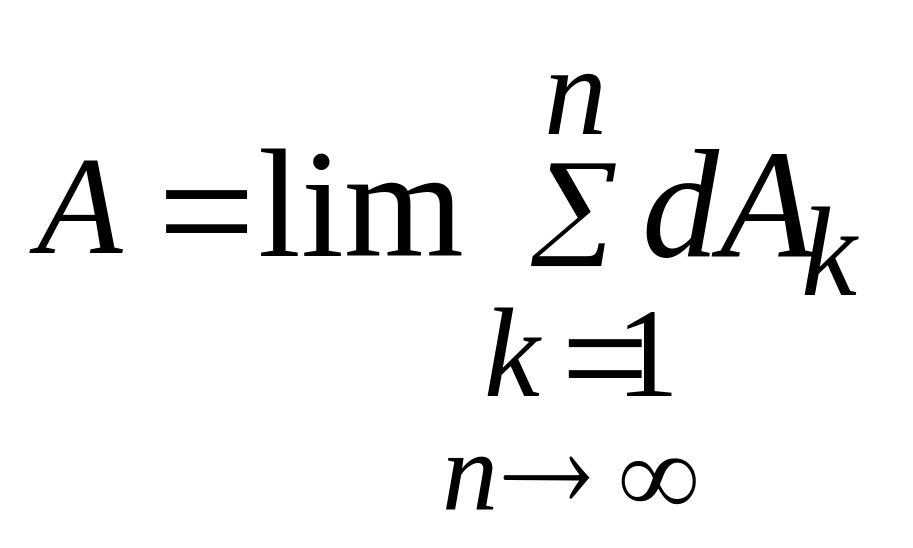где – работа на k-том элементарном перемещении, на которые разбито полное перемещение.

Так как эта сумма является интегральной суммой на кривой М₀М, то, используя для элементарной работы формулу , имеем

. (6.5)

Используя другие выражения для элементарной работы, полную работу силы получим в виде

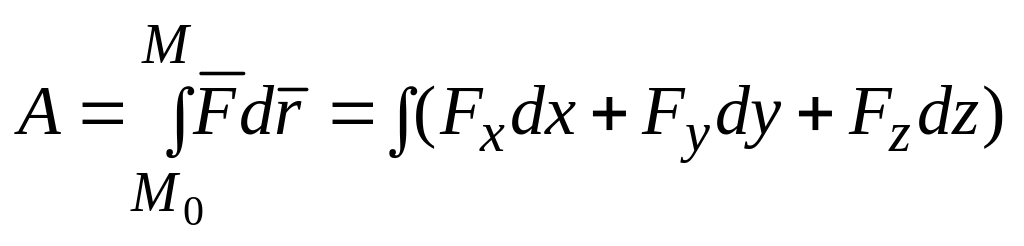, или , (6.6)

где t=0 для точки М₀, а t - для точки М.

Последняя формула удобна при вычислении работы, когда .

Отметим, что из определения элементарной и полной работы следует.

1) Работа равнодействующей на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

2) Работа силы на полном перемещении равна сумме ее работ на составляющих перемещениях, на которое любым образом разбито все перемещение.

Первое свойство достаточно доказать для элементарной работы равнодействующей силы.

Если сила - равнодействующая системы сил, то (равна их геометрической сумме). По определению элементарной работы силы, имеем

. (6.7)

В правой части каждый член представляет собой элементарную работу соответствующей силы в отдельности, то есть свойство подтверждено.

Второе свойство непосредственно следует из возможности разбиения любым образом полного промежутка интегрирования на составляющие, причем определенный интеграл по полному промежутку интегрирования равен сумме интегралов по составляющим.

Размерность полной работы такая, как и для элементарной работы: .

В технических системе единиц , в системе CИ .

Если , то из (6.5) следует

, (6.8)

где s - пройденный точкой путь.

Так как , то

.

Если при этом =0⁰ или =180⁰, то .

Эта формула применима как для криволинейного движения, так и для прямолинейного. Для этого необходимо, чтобы сила была постоянной величиной и всегда направлена по касательной к траектории. Если движение прямолинейное, то сила должна быть направлена по этой прямой.