Лекция 15

Устойчивость равновесия и движения механической системы.

Теорема Лагранжа-Дирихле об устойчивости равновесия. Малые колебания системы с одной степенью свободы

Устойчивость равновесия и движения механической системы

Существует три вида равновесия: устойчивое, неустойчивое, безразличное. Рассмотрим их и покажем условия устойчивого равновесия.

Ч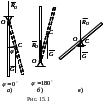 тобы установить, будет ли рассматриваемое положение устойчивым, следует дать стержню достаточно малое отклонение от положения равновесия (в общем случае сообщить ему ещё малую начальную скорость) и рассмотреть его последующее движение (рис. 15.1). Для простоты ограничимся одним только малым начальным отклонением от начального положения.

При отклонении стержня из положения равновесия сила тяжести и реактивная сила представляют собой неуравновешенную систему сил - пару сил, которая в случае а) будет стремиться вернуть стержень в положение равновесия, а в случае б) удалять от него.

Если существует такое достаточно малое начальное отклонение от положения равновесия, при котором силы стремятся вернуть стержень в положение равновесия, то это положение называется устойчивым (рис. 15.1-а).

Если силы ещё больше удаляют стержень от положения равновесия, то такое положение является неустойчивым (рис. 15.1-б).

Если стержень, получив любое малое начальное перемещение от положения равновесия, остается в равновесии в новом положении, такое положение равновесия называется безразличным (рис. 15.1-в).

В общем случае стержню следует сообщить некоторую достаточно малую начальную скорость. Тогда случай безразличного равновесия можно считать частным случаем неустойчивого равновесия, так как в таком положении равновесия стержень будет продолжать удаляться от своего первоначального положения равновесия с той же скоростью по инерции.

Изложенное характерно не только для любого твёрдого тела, но и для любой механической системы. Наибольший интерес представляет положение устойчивого равновесия, так как в положении равновесия тело или система могут находиться длительное время, пока им не сообщается какое-либо возмущение.

При устойчивом положении равновесия система, выведенная из него достаточно малыми возмущениями в виде начальных отклонений и скоростей, сообщённых всем точкам системы или их части, совершает колебания около положения равновесия или приближается к нему без колебаний. При неустойчивом положении равновесия случайные возмущения приводят к тому, что система ещё больше удаляется от него.

Точное понятие устойчивого положения равновесия системы было сформулировано для системы с конечным числом степеней свободы n в конце XIX века русским учёным А. М. Ляпуновым.

Положение системы определяется обобщёнными координатами , отсчитываемыми от положения равновесия, в котором они равны нулю (то есть их отсчет ведётся от положения равновесия). Начальное возмущение в общем случае состоит из начальных значений обобщённых координат и начальных скоростей .

Теорема А.М. Ляпунова: равновесие системы называется устойчивым, если для всякого как угодно малого положительного числа можно выбрать два других таких малых положительных числа и , что при начальных возмущениях, удовлетворяющих условиям

< и < ,

при дальнейшем движении механической системы выполняются условия

<

для каждой обобщенной ординаты.