Лекция 16

Явление удара. Действие ударной силы на материальную точку. Теорема об изменении количества движения системы. Удар шара о неподвижную поверхность. Коэффициент восстановления

Явление удара

По времени действия силы, действующие на МТ, разделяются на силы, изменяющие ее скорость за конечный промежуток времени (конечные силы, например, силы тяжести), и силы, изменяющие ее за малый промежуток времени (≤ 0,1 с) (мгновенные, или ударные, силы).

Мгновенной (ударной) силой называют силу, действующую на протяжении очень малого промежутка времени, но достигающую при этом таких больших значений, что ее импульс за это время успевает стать конечной величиной. Этот импульс

, (16.1)

где - время действия силы .

П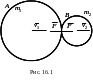 усть тело А, имеющее скорость , и тело В, имеющее скорость , соударяются (рис. 16.1). Движение тел до удара считаем поступательным и > . Общая нормаль к поверхностям соударяющихся тел в точке их соприкосновения называется линией удара.

Удар называется центральным, если центры масс соударяющихся тел лежат на линии удара. Центральный удар называется прямым, если скорости центров масс соударяющихся тел направлены по линии удара. Удар тел А и В предполагаем прямым центральным. Тела считаем абсолютно гладкими.

В процессе соударения оба тела деформируются, при этом скорость тела А уменьшается, а скорость тела В увеличивается. Процесс деформирования заканчивается тогда, когда скорости тел становятся одинаковыми. Эту часть удара называют фазой деформации, время ее продолжительности обозначим через .

Обозначим: - сила действия на тело А со стороны тела В, а - сила действия на тело В со стороны А.

Ударный импульс силы за фазу деформации

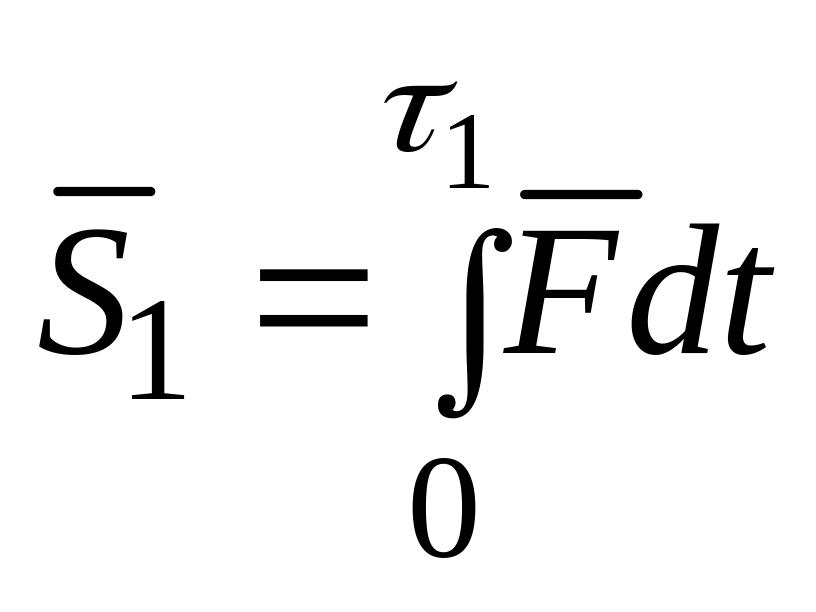. (16.2)

Импульс силы за то же время .

После деформации в силу упругости тела восстанавливают свои размеры и форму полностью или частично. Эту фазу называют фазой восстановления. Она заканчивается в момент отделения тел друг от друга. Обозначим - время фазы восстановления, тогда полное время удара

Импульс ударной силы, действующей на тело А, за фазу восстановления

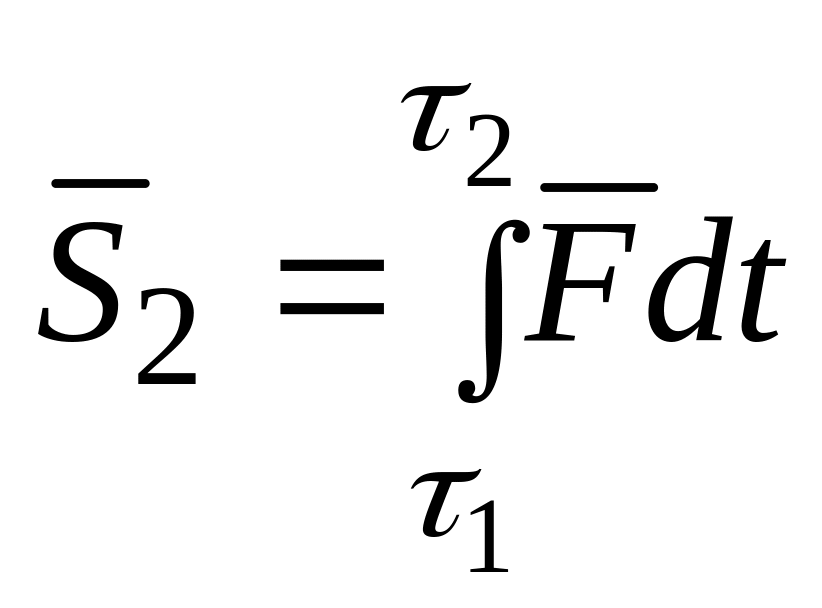. (16.3)

Действие ударной силы оцениваются по ударному импульсу, поэтому все теоремы об ударе формулируются так, чтобы в них входили ударные импульсы, а не ударные силы.

Упругость соударяющихся тел при ударе оценивается отношением ударного импульса за фазу восстановления к ударному импульсу за фазу деформации, называемым коэффициентом восстановления (безразмерная величина)

. (16.4)

Для реальных тел в природе эти значения находятся в пределах (определяются опытным путем).

Если , то есть , то фаза восстановления отсутствует, удар называется абсолютно неупругим. При , и тело восстанавливает полностью свои размеры и форму. Удар называется абсолютно упругим. При < <1 происходит удар тел средней упругости, и он называется упругим.