Лекция 11

Силы инерции материальной точки. Принцип Даламбера для

материальной точки и механической системы. Основы кинетостатики. Определение динамических реакций. Главный вектор и

главный момент сил инерции.

Силы инерции. Принцип Даламбера для мт

Рассмотрим дифференциальное уравнение движения материальной точки массой в некоторой инерциальной системе отсчета под действием приложенных к ней сил

, (11.1)

где – равнодействующая активных сил, - реакция связей, – ускорение точки.

Уравнение можно представить в виде

. (11.2)

Левая часть (11.2) представляет собой сумму векторов, имеющих размерность сил. Удобно вектор ( ) считать условной силой. Эту силу называют силой инерции точки в данной системе отсчета.

Силой инерции называется вектор, направленный противоположно ускорению точки и равный по величине произведению массы на модуль ускорения

.

Уравнение (11.2) можно представить в виде

.

Оно описывает состояние динамического равновесия МТ и выражает принцип Даламбера: при движении МТ непосредственно приложенная к ней сила, реакция связей и сила инерции точки составляют систему сил, эквивалентную нулю, то есть находящуюся в динамическом равновесии.

МТ движется с ускорением , так как на нее действуют тела с силой ( ).

П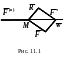 о закону о равенстве сил действия и противодействия МТ оказывает противодействие этим телам, характеризуемое силой – ( ), равной силе инерции (рис. 11.1).

Таким образом, сила инерции равна векторной сумме сил воздействия со стороны МТ на тела, которые сообщают ей движение с данным ускорением .

Силы инерции условно прикладывают к МТ и рассуждают о ее динамическом равновесии. Этот прием носит название «метод кинетостатики». Существуют и другие точки зрения на природу сил инерции [1,2].

Так как полное ускорение МТ можно разложить на касательную и нормаль (рис. 11.2)

,

т о силу инерции можно представить в виде геометрической суммы векторов

,

где - касательная сила инерции, направленная по касательной к траектории точки; - нормальная (центробежная) сила инерции, направленная по нормали к траектории в сторону ее выпуклости.

Принцип Даламбера для механической системы

Для каждой из N материальных точек механической системы можно написать

(к=1,2,3,…,N). (11.3)

Эти соотношения выражают принцип Даламбера для системы МТ: в движущейся механической системе система активных сил, реакций связей и сил инерции удовлетворяет условиям равновесия, то есть представляют собой систему сил, главный вектор и главный момент которой относительно любого центра равны нулю.

Из принципа Даламбера можно получить следствия в виде шести условий равновесия, которые формально аналогичны условиям равновесия статики для сил, приложенных к твердому телу. Просуммировав выражение (11.3) для всех МТ системы, получим

(11.4)

Умножив на радиус-вектор каждый из членов соотношения (11.3) и суммируя их, получим

,

или

. (11.5)

Проекции (11.4) и (11.5) на оси имеют вид

(11.6)

Представляя равнодействующую силу, приложенную к каждой точке системы, как состоящую из внешней и внутренней силы, получим

.

Следовательно, на основании (11.4) и (11.5) имеем

,

, (11.7)

так как главный вектор и главный момент внутренних сил равны нулю.

Положительной особенностью этих соотношений является отсутствие внутренних сил, что делает их удобными при решении задач динамики системы.