Количество движения системы

Напишем выражение, определяющее положение центра масс системы,

.

Продифференцировав по времени левую и правую части, имеем

, или .

Так как , а , то

, (9.1)

то есть количество движения механической системы равно количеству движения ее центра масс в предположении, что в нем сосредоточена вся масса системы (рис. 9.1).

С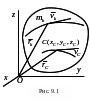 проектируем соотношение (9.1) на координатные оси

, , (9.2) .

Проекция на любую ось количества движения механической системы равна проекции на ту же ось количества движения ее центра масс в предположении, что в нем сосредоточена вся масса системы.

Теорема об изменении количества движения системы

Напишем теорему об изменении количества движения МТ, выделив внешние и внутренние силы,

, (9.3)

где и - равнодействующие внешних и внутренних сил, действующих на МТ.

Составим по аналогии эти выражения и для других МТ системы, сложим их левые и правые части, соответственно,

.

Заметим, что

, .

Следовательно,

. (9.4)

Получена теорема об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме внешних сил, действующих на систему.

Спроектируем соотношение (9.4) на координатные оси

, , ,

то есть производная по времени от проекции количества движения системы на какую-либо ось равна алгебраической сумме проекций всех внешних сил, действующих на систему.

Умножив обе части соотношения (9.4) на dt, получим

, (9.5)

то есть дифференциал количества движения системы равен векторной сумме элементарных импульсов внешних сил, действующих на систему.

В проекциях на координатные оси

, , . (9.6)

Беря интеграл от обеих частей (9.5), имеем

. (9.7)

Получена теорема об изменении количества движения механической системы в конечной форме: изменение количества движения системы за какой-то промежуток времени равно векторной сумме импульсов всех внешних сил, действующих на систему, за то же время.

В проекциях на координатные оси аналогично

, , . (9.8)

Отметим следующее.

1. Внутренние силы не входят в теорему об изменении количества движения системы и, следовательно, не влияют на его величину.

2. При некоторых условиях для внешних сил можно получить первые интегралы системы дифференциальных уравнений движения системы.

Следствие. Закон сохранения количества движения системы.

Положим, что , тогда .

Если в течение некоторого времени главный вектор внешних сил, действующих на систему, равен нулю, то количество движения системы за это время остается постоянным.

Для проекций на координатные оси аналогично. Например, если , то .

Если в течение некоторого времени алгебраическая сумма проекций на какую-либо ось внешних сил, действующих на систему, остается равной нулю, то проекция на ту же ось количества движения системы за это время остается постоянной величиной.