Две основные задачи динамики материальной точки

1-я задача. Зная массу МТ и закон ее движения, требуется найти действующую на точку силу.

Положим, известны законы движения вдоль координатных осей

, , . (1.11)

Проекции силы на оси

, , . (1.12)

Следовательно, модуль вектора силы

. (1.13)

Направляющие косинусы

, , . (1.14)

Заметим, что реакции связей входят как составляющие в силу .

2-я задача. По заданной массе и действующей на МТ силе требуется определить закон движения точки.

Напишем выражение ускорения

. (1.15)

Дважды интегрируя по времени, находим закон движения точки вдоль траектории .

Лекция 2

Интегрирование дифференциальных уравнений движения

материальной точки в простейших случаях. Постоянные

интегрирования и их определение из начальных условий.

Прямолинейное колебательное движение материальной точки. Свободные колебания. Амплитуда, фаза, круговая частота и период

Вторая задача динамики точки

Эта задача связана с интегрированием дифференциальных уравнений движения МТ. Рассмотрим решение задачи в прямоугольной декартовой системе координат (рис. 2.1).

П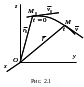 усть в общем случае сила и ее проекции на оси зависят от времени, положения точки и ее скорости. Тогда дифференциальные уравнения в проекциях на оси

,

, (2.1)

.

Решение сводится к интегрированию системы трех обыкновенных дифференциальных уравнений второго порядка. Известно, что решение одного такого уравнения содержит две произвольные постоянные интегрирования. Всего для системы их окажется шесть: .

Решение представляется в виде

,

, (2.2)

.

Если продифференцировать систему (2.2) по времени, то проекции скорости точки на координатные оси

,

, (2.3)

.

Таким образом, задание силы определяет целый класс движений, характеризующийся произвольными постоянными. Действующая сила определяет лишь ускорение точки. Для определения движения необходимо располагать дополнительно начальными условиями, позволяющими определить произвольные постоянные. При задаются начальные координаты и проекции скорости .

Используя эти условия, на основании (2.2), (2.3) можно написать шесть уравнений для определения постоянных

,

,

, (2.4)

,

Если система (2.4) удовлетворяет условиям разрешимости, то из нее можно найти все шесть произвольных постоянных интегрирования.

План решения второй задачи динамики.

1. Выбираем систему отсчета. Ее начало желательно разместить в начальном положении точки. Желательно также, чтобы в рассматриваемый момент времени координаты точки и проекции скорости на оси были положительны. В естественных координатах за их начало принимается сама точка.

2. Составляется расчетная схема. Изображается точка с действующими на нее активными и реактивными силами.

3. Записываются начальные условия.

4. Составляются дифференциальные уравнения в проекциях на координатные оси. При этом в правой части записываются алгебраические суммы проекций всех сил, действующих на точку, с обязательным указанием тех параметров, от которых они зависят.

5. Производится интегрирование дифференциальных уравнений.

6. С помощью начальных условий находятся произвольные постоянные, которые целесообразно определять после каждого интегрирования. В отдельных случаях удобно брать определенный интеграл в заданных пределах.

7. С нахождением закона движения определяются искомые в задаче величины.