2.6.1 Геометрический метод решения задач линейного программирования со многими переменными

Геометрические соображения могут быть полезными при решении задач линейного программирования со многими переменными, а именно, когда в рассматриваемой задаче линейного программирования число переменных больше числа ограничений, записанных в форме равенств, не более чем на 2. Пусть, например, дана задача линейного программирования в следующей постановке.

f (x) = (2.10)

на множестве X = {x

, i = 1,…,l; x _j 0, j = 1,…, n.}, (2.11)

где n – l = 2, причем ранг матрицы А = // a _{m+i j} // равен l. i = 1,…,l; j = 1,…, n

Тогда, используя метод Жордана–Гаусса (метод исключения неизвестных), производим в системе ограничений-равенств

, i = 1,…,l,

l исключений, в результате которых l =n – 2 переменных выразятся через оставшиеся две переменные, скажем через x₁ и x₂, т. е.

x _j= p_j1 x₁ + p_j2 x₂+b_i, j =3,4,…,n, (2.12)

где p_{j 1,} p_{j 2}, b_i - некоторые числа. Подставляя эти выражения в целевую функцию f и систему ограничений – неравенств

, i = 1,…, m,

получаем уже задачу линейного программирования с двумя переменными:

(2.13)

на множестве , i =1,…, m; p_j1 x₁+ p_j2 x₂ + β_j ≥ 0, j=3,4,…, n ; x₁≥ 0, x₂≥ 0.}, где α _i1 ,α _i2, θ _i (i = 1,…, m), γ_1, γ₂, δ – некоторые числа.

Далее с помощью геометрических построений находим ее решение (x₁^*, x₂^*). Затем подставляем эти числа в (2.12) и (2.13), в результате получаем оптимальное решение и значение целевой функции исходной задачи (2.10) - (2.11).

Описанный метод исключения переменных, конечно, применим и в том случае, если в задаче (2.10) - (2.11) n-l=1. Тогда все сводится к описанию решения элементарной задачи линейного программирования с одной переменной. Если в задаче (2.10) - (2.11) на все переменные x_j, j=1,…,n, наложено условие неотрицательности, то это приводит к уменьшению числа ограничений вида p_j1 x₁+p_j2x₂+β_j ≥ 0.

Пример 2. 5. 1.

На металлургическом заводе производится чугун из материала треx видов, отличающихся друг от друга содержанием серы, фосфора, марганца и стоимостью:

Таблица 6

Вид шиxтового материала	Содержание в 1 ед. шиxтового материала компонента (%)			Стоимость 1 ед. шиxтового материала
	сера	фосфор	марганец
А1	15	30	50	10
А2	10	25	60	15
А3	8	17	70	12

Остальные 5 % шиxтового материала каждого вида составляют другие компоненты. Определить оптимальный набор шиxтового материала, при котором можно получить с наименьшими затратами чугун, содержащий не менее 12 % серы, не более 28 % фосфора и не более 60 %марганца.

Математическая формулировка задачи

Обозначим через x_j, j = 1, 2, 3, количество шиxтового материала вида А _j, необxодимое для получения 1ед. чугуна. Тогда математическая модель приведенной задачи запишется в виде:

минимизируется стоимость 1 ед. чугуна

f (x) = 10 x₁+ 15 x₂ +12 x₃ → min

на множестве ограничений на содержание компонентов в чугуне

1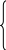 5 x ₁ +10 x₂+ 8 x₃ ≥ 12

30 x ₁ + 25 x₂ + 17 x₃ 28

50 x ₁ +60 x₂ + 70 x₃ 60

x ₁+ x₂+ x₃ = 1

x_j ≥ 0, j = 1,2,3

Замечаем, что в данной модели число переменных равно n=3, и имеется ограничение – равенство, следовательно, n–1=2. Поэтому из имеющихся равенств выражаем одну переменную, например, x₁=1-x₂–x₃≥0. Затем подставляем полученное значение переменной x₁ в целевую функцию f(x) и в оставшиеся неравенства множества X.

f(x)=10-10х₂-10х₃+15х₂+12х₃=10+5х₂+2х₃ min

х₁=1-х₂-х₃

1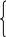 5-15х₂-15х₃+10х₂+8х₃ 12 или 5х₂+7х₃ 3

30-30х₂-30х₃+25х₂+17х₃  28 или 5х₂+13х₃  2

50-50х₂-50х₃+60х₂+70х₃ 60 или 10х₂+20х₃ 10

х₂+х₃ 1

Последнее неравенство получено из условия, что х₁ 0.

В результате получаем задачу линейного программирования уже с двумя переменными x₂ и x₃:

min

на множестве:

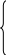5 x₂+7x₃  3 (1)

5 x₂+13x₃  2 (2)

x₂+2x₃  1 (3)

x₂+x₃  1 (4)

x ₂ 0 ; x ₃ 0

П остроим допустимое множество и линии уровня целевой функции в системе координат x₂ x₃ (рис10). На рисунке видно, что линейная функция принимает минимальное значение в вершине А ОДР ABCD. Координаты этой вершины отыскиваем, решая систему уравнений граничных прямых 5 x₂+13x₃ =2

x₂=0

Отсюда x₂^* = 0; x₃^* = 2/13, т.е. А (0;2/13), и минимальное значение функции f ^* = (x₂^*; x₃^*)= 10+50+2 = ($)

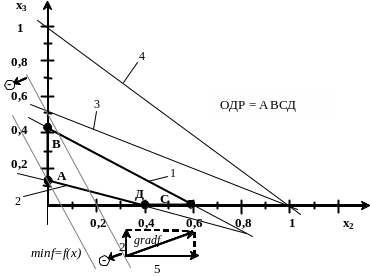
Рис.10. Графическое решение задачи

Определяем оставшуюся компоненту оптимального решения исходной задачи X^* = (x ₁^*, x ₂^*, x ₃^*):

x ₁^* = 1- x ₂^* -x ₃^* =1-0- =

Таким образом, для получения 1 ед. чугуна с наименьшей себестоимостью, равной долл., необходимо использовать ед. шихтового материала вида А₁ и единиц шихтового материала вида А₃. Использование же шихтового материала вида А₂ является экономически невыгодным. При этом полученный чугун будет содержать:

14% серы;

28% фосфора; 53% марганца.

Пример 2. 5. 2.

В течение квартала планируется выпуск двух видов продукции. Фирма может оплатить материалы и труд (себестоимость) из двух источников – собственных и заемных средств. Собственные средства фирмы составляют 30000$. Банк может ссудить до 20000$ под 5% с условием погашения ссуды в конце квартала. Производственные мощности фирмы, цены и себестоимость продукции содержатся в таблице:

Таблица 7

Вид про-дукции	Цена реализации ед. продукции	Себестоимость ед. продукции	Трудозатраты на технологические операции (час на 1 ед.)
			Операция А	Операция В	Операция С
1	14$	10$	0,5	0,3	0,2
2	11$	8$	0,3	0,4	0,1
Ресурсы фирмы (час в квартал)			540	500	350

Определить объемы выпуска продукции 1 и 2 и объем заемных средств, максимизирующих прибыль, если известно, что отношение объемов выпуска продукции 1 и 2 равно 2:1.

Математическая формулировка задачи

Обозначим через х_i – количество продукции вида i (i=1,2),

х₃ – объём заёмных средств.

Целевая функция:

f (x) = (14 – 10) х₁ + (11- 8) х₂ – 1,05 х₃= 4х₁+3х₂-1,05х₃ → max .

З атраты на материалы и труд:

10 х₁ + 8 х₂ ≤30 000+х₃ (1)

Величина заемных средств:

х₃ ≤ 20 000 (2)

Производственные ограничения (в часах):

0,5 х₁ + 0,3 х₁ ≤ 540 (3)

0,3 х₁ + 0,4 х₂ ≤ 500 (4)

0,2 х₁ + 0,1 х₂ ≤ 350 (5)

Объемы выпуска

х₁ = 2 х₂ (6)

х_i ≥ 0, i=1,2,3

С учетом ограничения х₁=2х₂ придем к задаче с двумя неизвестными:

f (x) = 4х₁+3х₂–1,05х₃=42х₂+3х₂–1,05х₃= 11х₂–1,05 х₃ → max .

2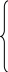 8х₂–х₃ ≤ 30000 (1) при х₂=0 х₃=-30000;

при х₃=0 х₂=1071,4

х₃ ≤ 20000 (2) х₃=20000

1,3х₃ ≤ 540 (3) х₃=415,4

х₂ ≤ 500 (4) х₂=500

0,5х₂ ≤ 350 (5) х₂=700

х_i ≥ 0, i=2,3

В целевой функции коэффициент при х₃ отрицательный, требуется max прибыль, т.е. в оптимальном решении х₃=0.

При х₃=0, достигается max прибыль в т.А (рис.11)

х ₁*=830,8

х₂*=415,4

х₃*=0

max f (х^*)= 11^. 415,4-1,05^. 0=4569,4

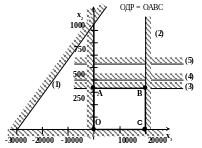
Рис.11. Графическое решение задачи

Пример 2. 5. 3.

Менеджер желает приобрести акции трех ведущих предприятий, которые могут дать месячный доход, равный соответственно 11%, 15% и 8%. Риски при вложении капитала для приобретения данных акций определены рынком и равны соответственно 1; 1,2; 0,9. Требуется, чтобы средняя взвешенная этих рисков была не более 1,1. Менеджеру необходимо определить такие доли вложения своего капитала при покупке акций, которые приведут к получениию максимального дохода.

Математическая формулировка задачи

Обозначим: х_i – количество акций i–го предприятия;

р_i - вероятность получения дохода;

Математическое ожидание месячного дохода f:

f=

x₁+x₂+x₃=1 (1)

x₁+1,2x₂+0,9x₃ 1,1 (2)

x_i 0 i=1,...,3

Выразим из (1) х₁=1-х₂-х₃0.

Тогда f(x)=11-11x₁-11x₃+15x₂+8x₃=11+4x₂-3x₃ max

Так как коэффициент при х₃ отрицательный, то в оптимальном решении х₃=0. Убедимся в этом решив задачу графическим методом (рис.12)

Так как х₁0, то получим: 1-х₂-х₃ 0

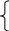х₂+х₃ 1 (1)

1-х₂-х₃+1,2х₂+0,9х₃  1,1 или 0,2х₂-0,1х₃ 0,1 (2)

х₂, х₃0

max f = f(C), т.е. оптимальный доход достигается в точке С с координатами (0,5;0).

Тогда f(C)= 11+4^. 0,5 – 3^. 0 = 13, оптимальный план Х^*= (0,5;0,5;0).

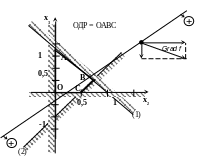
Рис. 12. Графическое решение задачи