ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

АНГАРСКАЯ ГОСУДАРСТВЕННАЯ ТЕХНИЧЕСКАЯ АКАДЕМИЯ

Экономикоматематические методы

ЧАСТЬ ПЕРВАЯ

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Учебное пособие

АГТА, 2005 г

Линейное программирование. Часть первая. Учебное пособие по курсу ″Экономикоматематические методы.″

Учебное пособие составили В.С. Асламова, И.М. Елькина Ангарск 2005 г.

Данное учебное пособие посвящено изучению линейных математических моделей, способов их построения и методов расчета. На многочисленных примерах подробно и доступно объяснены математические методы решения задач линейного программирования. Рассмотрено решение олимпиадных задач.

Пособие предназначено студентам экономических и некоторых технических специальностей вузов, а также преподавателям и аспирантам.

рецензент к.т.н., проф. А.Л. Истомин

рекомендовано к изданию учебно-методическим советом АГТА.

 АГТА, 2005.

СОДЕРЖАНИЕ

Введение 5

1 Особенности моделирования экономических процессов 6

1.2.1 Сущность процесса моделирования 6

1.3.1 Характерные особенности математического моделирования в экономике 8

1.4.1 Классификация математических моделей 10

1.5.1 Этапы исследования экономических процессов 14

2 Линейные математические модели 16

2.2.1 Примеры постановок задач линейного программирования 16

2.3.1 Формы представления задач линейного программирования 30

2.4.1 Геометрический метод решения задач линейного программирования 34

2.5.1 Модифицированный геометрический метод 37

2.6.1 Геометрический метод решения задач линейного программирования со многими переменными 42

2.7.1 Виды оптимальных решений 49

2.8.1 Основы анализа модели на чувствительность 53

M 61

2.9.1 Симплексный метод решения задач линейного программирования 67

2.10.1 Особые случаи применения симплекс - метода 79

2.9.1. Вырожденность. 79

2.9.2. Зацикливание. 81

2.9.3. Альтернативные оптимальные решения 82

2.9.4. Неограниченные решения. 84

2.9.5. Отсутствие допустимых решений 87

2.11.1 Интерпретация симплекс-таблиц – анализ модели на чувствительность 90

2.12.1 Искусственное начальное решение 98

2.9.1. Метод больших штрафов 98

2.9.2. Двухэтапный метод 101

2.9.3. Двойственный симплекс-метод 106

2.13.1 Двойственная задача линейного программирования 108

Список литературы 127

Приложение 1. Блок-схема симплекс-метода 128

Приложение 2. Блок-схема метода больших штрафов 132

Приложение 3. Блок-схема двойственного симплекс-метода 137

Введение

Экономические проблемы, возникающие перед специалистами в боль­шинстве своем сложные. Они зависят от множества различных, иногда противоречащих друг другу факторов, изменяются с течением времени и влияют на другие проблемы и процессы.

Вследствие этого исследование экономической проблемы целесо­образно проводить на адекватной математической модели. Математическая модель отражает проблему в абстрактной форме и позволяет учесть большое число разнообразных характеристик, от которых зависит эта проблема. Анализ и расчет математической модели позволяют выбрать оптимальные решения поставленной задачи и обосновать этот выбор.

Успешная реализация достижений научно-технического прогресса в нашей стране тесным образом связана с использованием математических методов и средств вычислительной техники при решении задач из различных областей человеческой деятельности. Исключительно важное значение приобретает использование указанных методов и средств при решении экономических задач. Данное учебное пособие посвящено изучению различных математических моделей, способов их построения, методов расчета и применению для решения экономических задач. В нем на многочисленных примерах подробно и доступно объяснены математические методы расчета представленных моделей.

В первой главе рассмотрены принципы и этапы построения математических моделей, их место в научном исследовании проблемы. Дана классификация математических моделей по критериям оптимальности, структуре ограничений, учету неизвестных факторов, виду неопределен­ности. Вторая глава пособия посвящена вопросам линейной оптимизации, таким как линейное программирование, постановка и решение двойственных задач.

В популярной форме даны общая постановка задачи, построение для нее математической модели и методы ее решения. Приведены примеры конкретных расчетов. Представлены экономические проблемы, оптимальное решение которых возможно после использования соответствующей математической модели (это задачи оптимального планирования инвестиций, формирование минимальной потребительской корзины и целый ряд других).

Пособие предназначено студентам экономических и некоторых технических специальностей вузов, а также преподавателям и аспирантам.

1Особенности моделирования экономических процессов

1.2.1Сущность процесса моделирования

В связи с развитием производства возрастает объем экономических расчетов, повышаются требования к их точности. Все глубже внедряются в экономику математические методы.

Термин "модель" широко используется в различных областях человеческой деятельности. Модель - это такой материально или мысленно представляемый объект, который в процессе исследования замещает объект оригинал так, что непосредственное изучение модели дает новые знания об объекте-оригинале.

П

Этап 1

Построение модели

од моделированием понимается процесс построения, изучения и применения модели. Процесс моделирования включает три элемента: субъект (исследователь), объект исследования и модель. Сущность процесса моделирования схематично изображена на рис.1.

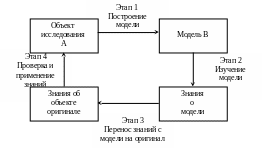
Рис.1. Этапы процесса моделирования

Этап 1 предполагает наличие некоторых знаний об объекте А. Познавательные возможности модели В обуславливаются тем, что модель имитирует (отображает) какие-либо существенные черты объекта-оригинала. На 2-м этапе процесса модель выступает как объект исследования. На 3-м этапе осуществляется перенос знаний с модели на оригинал. При этом знания должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели. Если же определенный результат связан с отличием модели от оригинала (неадекватностью), то этот результат переносить неправомерно. На 4-м этапе производится практическая проверка полученных с помощью модели знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.

Моделирование - циклический процесс. Это означает, что за первым четырехэтапным циклом могут последовать и другие. При этом знания об исследуемом объекте расширяются, уточняются, а исходная модель постепенно совершенствуется.