2.7.1 Виды оптимальных решений

Тот факт, что оптимальное решение находится в вершине ОДР, дал нам возможность сформулировать метод решения задач линейного программирования. Но из этого же факта можно сделать еще два очень важных вывода. Во-первых, если оптимальным решением являются координаты вершины ОДР, значит, столько оптимальных решений может иметь задача. Во-вторых, поскольку чем больше ограничений, тем больше вершин, то, следовательно, чем больше ограничений, тем больше оптимальных решений. Как видно из рис.14.а, вершина, координаты которой являются оптимальным решением, определяется углом наклона прямой, описывающей целевую функцию. Значит, каждая вершина будет соответствовать оптимальному решению для некоторой целевой функции.

Рис. 13

Поясним это на примере. Пусть для двух видов продукции П₁ и П₂ требуются трудовые, материальные, финансовые ресурсы. Наличие ресурсов каждого вида и их нормы расхода, необходимые для выпуска единицы продукции, приведены в табл.8.

Таблица 8

Характеристика	Вид продукции		Располагаемый ресурс
	П1	П2
Резервы: Трудовые Материальные Финансовые Выпуск Прибыль План	1 3 6 1 4 х1	4 4 2 1 8,5 х2	14 18 27 _ _ _

Составим математическую модель задачи. Ограничения и граничные условия, входящие в модель этой задачи, будут иметь вид:

х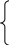 ₁+4х₂ 14;

3х₁+4 х₂ 18;

6 х₁+2 х₂ 27;

х₁ 0; х₂ 0;

Найдем оптимальные решения для пяти целевых функций:

максимизация суммарного выпуска f₁= х₁+ х₂ maх

максимизация выпуска продукции П₂ f₂= х₂ maх

максимизация выпуска продукции П₁ f₃= х₁ maх

максимизация прибыли f₄=4 х₁+8,5 х₂ maх

минимизация используемых ресурсов f₅=(1+3+6)х₁+(4+4+2) х₂ min

т.е. f₅=10 х₁+10 х₂ min

Для каждой приведенной целевой функции можно построить линию целевой функции и определить вершину, в которой целевая функция будет иметь оптимальное значение. Результаты решения задачи по пяти целевым функциям сведены в таблицу 9, из анализа которой можно сделать вывод: координаты каждой вершины могут быть оптимальным решением задачи в некотором принятом смысле.

Так, вершина С дает максимальный суммарный выпуск, вершина А – максимальный выпуск продукции П₂ и т.д.

Таблица 9

Целевая Функция	Вершина	х1	х2	х1+ х2	Прибыль	Используе-мый ресурс
f1= х1+ х2 мах	C	4	1,5	5,5	28,75	55
f2= х2 мах	A	0	3,5	3,5	29,75	35
f3= х1 мах	D	4,5	0	4,5	18	45
f4=4х1+8,5х2 мах	B	2	3	5	33,5	50
f5=10х1+10х2 min	F	0	0	0	0	0

Рассмотрим далее, как влияет на оптимальное решение введение дополнительных ограничений. Пусть дана задача, которая графически представлена на рис 14,а

Рис. 14,а

Принимаем, что при максимизации оптимальное решение находится в вершине В и имеет значения х₁⁰, х₂⁰, f₀. Рассмотрим, как влияют на оптимальное решение дополнительные ограничения, например, применительно к х₁.

Таблица 10

Номер рисунка	х зад	Дополнительное ограничение	мах f
рис.14,б	х зад< х10	х1 х зад	f1<f0
рис.14,в	х зад< х10	х1 х зад	f2=f0
рис.14,г	х зад> х10	х1 х зад	f3<f0
рис.14,д	х зад> х маx	х1 х зад	Нет

Из рис 14 и табл.10 видно следующее: дополнительное ограничение ухудшило целевую функцию (рис 14,б), оптимальное решение не изменилось (рис 14,в), оптимальное решение ухудшилось (рис 14,г), характерно появились несовместности (рис 14,д), которое привело к тому, что задача вообще не имеет решения.

Подытоживая влияние дополнительных ограничений на оптимальное решение, можно отметить три варианта: дополнительное ограничение не влияет на значение целевой функции, ухудшает ее, создает несовместность, т.е. исключает возможность получения даже допустимого решения. Можно сформулировать еще короче: дополнительное ограничение никогда не улучшает оптимального решения.

Значит, если мы хотим улучшать принятую целевую функцию, т.е. результат работы, мы должны стремиться к тому, чтобы иметь как можно меньше ограничений.