2.9.2. Двухэтапный метод

Недостаток M-метода связан с возможностью ошибок в вычислениях, обусловленной очень большой величиной коэффициента M. Например, если принять M=100000, тогда коэффициенты при х₁ и х₂ в f-уравнении начальной симплекс таблицы будут равны (-4 + 700000) и (-1 + 400000) соответственно. Из-за большой величины M вклад коэффициентов C₁= 4 и C₂= 1 при х₁ и х₂ оказывается ничтожно мал. Поэтому возникает опасность, что переменные х₁ и х₂ будут интерпретироваться как переменные, фигурирующие в целевой функции с нулевыми коэффициентами.

Двухэтапный метод позволяет избежать этих затруднений. В нем так же вводятся искусственные переменные, но без коэффициента M. Решение задачи расчленяется на два этапа.

Этап 1. Искусственная переменная вводится для получения начального базиса. Записывается новая целевая функция f₁, предусматривающая минимизацию суммы искусственных переменных при исходных ограничениях, видоизмененных за счет введения искусственных переменных.

Если минимальное значение новой целевой функции равно нулю, (то есть искусственные переменные равны нулю), то исходная задача имеет допустимое решение. Переходят тогда к этапу 2.

Если min f₁ 0, то исходная задача не имеет допустимых решений.

Этап 2. Оптимальное базисное решение, полученное на этапе1, используется в качестве начального базиса исходной задачи.

Пример 2. 11. 1: Рассмотрим предыдущий пример:

f₀= 4х₁ + х₂  min

при ограничениях:

3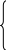 х₁ + х₂+R₁=3 (1)  R₁=3 – 3х₁ – х₂

4х₁ + 3х₂ -х₃+R₂= 6 (2)  R₂=6 – 4x₁-3х₂+х₃

х₁+2х₂+х₄=4 (3)

R₁, R₂0

x_i 0 i=1, 2,..,4

R₁+R₂=9-7х₁-4х₂+х₃

Этап 1. Решается задача f_1ур = R₁ + R₂ min.

Тогда целевая функция

f_1ур = 9 – 7х₁ – 4х₂ + х₃min

при ограничениях исходной задачи

Составим исходную симплекс - таблицу, за начальный базис возьмем R₁, R₂, х₄, свободные переменные

х₁ = х₂ = х₃ = 0

f_1ур – х₃+ 7х₁ + 4х₂ = 9

Таблица 37

№ итер	Базис	х1	х2	х3	х4	R1	R2	Знач	Отнош	Формула
№=0 х1 вв., R1 искл.	f1ур	7	4	-1	0	0	0	9
	R1	3	1	0	0	1	0	3	3:3=1
	R2	4	3	-1	0	0	1	6	6:4=3/2
	x4	1	2	0	1	0	0	4	4:1=4
№=1 х2 вв., R2 искл.	f1ур	0	5/3	-1	0	-7/3	0	2		f1ур=f1ур-7х1
	х1	1	1/3	0	0	1/3	0	1	1:1/3=3	х1=R1:3
	R2	0	5/3	-1	0	-4/3	1	2	2:5/3=6/5	R2=R2-4x1
	x4	0	5/3	0	1	-1/3	0	3	3:5/3=9/5	x4=x4-x1
№=2 оптим. решен. 1 этапа	f1ур	0	0	0	0	-1	-1	0		f1ур=f1ур-5/3х1
	х1	1	0	1/5	0	3/5	-1/5	3/5		х1= х1-1/3x2
	x2	0	1	-3/5	0	-4/5	3/5	6/5		x2=R2:5/3
	x4	0	0	1	1	1	-1	1		x4=x4-5/3x2

R₁^*=R₂^*= 0 х₁^*=3/5; х₂^*=6/5; х₃^*=0; x₄^*=1; f_1ур ^*= 0

Получили допустимое базисное решение исходной системы ограничений, так как f_1ур ^*= 0 при R₁^*=R₂^*= 0.

Этап 2. Искусственные переменные уже выполнили свою функцию, так что во всех последующих вычислениях они не должны фигурировать. Запишем из оптимальной симплекс таблицы уравнения ограничения:

х ₁+ х₃=  х₁= - х₃

х₂- х₃=  х₂= + х₃

х₃+х₄=1

Главная цель первого этапа обеспечить получение начального решения исходной системы ограничений. Теперь исходная задача содержит n = 4 переменных и m = 3 уравнения. Значит, число небазисных переменных n - m = 1. В полученном допустимом решении свободная переменная х₃= 0, базисная

х₁= , х₂= , х₄= 1.

Выразим целевую функцию через свободную переменную х₃, подставив выражения для базисных переменных х₁ и х₂ через небазисную переменную х₃.

f₀ = 4х₁ + х₂ = - х₃+ + х₃= - х₃ min

f_0ур х₃=

В результате будем иметь начальную симплекс - таблицу для 2–го этапа.

Таблица 38

№ итер.	Базис	х1	х2	х3	х4	Знач	Отнош	Формула
№=3 x3 вв., х4 искл.	f0ур	0	0	1/5	0	18/5
	х1	1	0	1/5	0	3/5	3/5:1/5=3
	х2	0	1	-3/5	0	6/5	не рассчит.
	х4	0	0	1	1	1	1:1=1
№=4 оптим. реше-ние	f0ур	0	0	0	-1/5	17/5		f0ур=f0ур-1/5х3
	х1	1	0	0	-1/5	2/5		х1=х1-1/5х3
	х2	0	1	0	3/5	9/5		х2=х2+3/5x3
	х3	0	0	1	1	1		x3=x4

Полученное решение оптимально, так как коэффициент при х₄<0, а решается задача minf₀

х₁^*= , х₂^*= , х₃^*= 1, х₄^*=0

min f₀ = 4х₁^* + х₂^* = 4 + = .

Замечание:

1) Количество необходимых итераций в М – методе и двухэтапном методе всегда одинаково (в нашем случае 3 итерации), а между симплекс-таблицами, которые получаются при использовании этих методов, имеется взаимнооднозначное соотношение.

2) На 2 этапе искусственные переменные отсутствуют только в том случае, если в конце 1 этапа они стали не базисными. Однако возможен случай, который при завершении 1 этапа искусственные переменные, имея нулевые значения, останутся базисными.

Пример 2. 11. 2:

Математическая модель

f₀=3х₁+2х₂+3х₃min

при ограничениях:

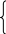х₁+4х₂+х₃  7

2х₁+х₂+х₄  10

х_i  0 i=1,..,4

В канонической форме

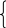х₁+4х₂+х₃х₅+R=7  R =7х₁4х₂х₃+х₅

2х₁+х₂+х₄х₆=10

х_i 0 i=1, 2,..,6; R 0

В качестве базисных переменных возьмем R и х₄, которые входят лишь в одно ограничение.

Первый этап:

f_1ур =R=7х₁4х₂х₃+х₅min

п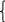 ри ограничениях:

х₁+4х₂+х₃х₅+R=7

2х₁+х₂+х₄х₆=10

f_1ур х₁ + 4х₂+х₃ х₅=7

Таблица 39

№ итер.	Базис	х1	х2	х3	х4	х5	х6	R	Знач	Отнош	Формула
N=0 x2 вв, R искл.	fур	1	4	1	0	-1	0	0	7
	R	1	4	1	0	-1	0	1	7	7:4=7/4
	х4	2	1	0	1	0	-1	0	10	10:1=10
N=1 оптимум	fур	0	0	0	0	0	0	-1	0		f1ур=f1ур-4x3
	х2	1/4	1	1/4	0	-1/4	0	1/4	7/4		x2=R:4
	X4	7/4	0	-1/4	1	1/4	-1	-1/4	3		x4=х4-х2

Второй этап:

Выразим базисную переменную х₂ через небазисные переменные. Из оптимальной симплекс–таблицы первого этапа:

х₁+х₂+ х₃ х₅ =  х₂=  х₁ х₃+ х₅

Подставим х₂ в f₀:

f₀=3х₁+2х₂+3х₃=3х₁+2(  х₁ х₃+ х₅)+3х₃=3х₁+  х₁ х₃+ х₅+3х₃== х₁+ х₃+ х₅+  min

В целевую функцию f₀ свободные переменные х_1, х₂, х₅ входят с положительными коэффициентами, поэтому их увеличение нецелесообразно, т.е. min f₀= при плане Х*=(0; ; 0; 3; 0)