2.9.1 Симплексный метод решения задач линейного программирования

При анализе графического метода было отмечено, что оптимальному решению соответствует одна из угловых точек области допустимых решений. Именно этот результат положен в основу симплексного метода. В его вычислительной схеме реализуется порядок, при котором, начиная с исходной допустимой угловой точки, осуществляются последовательные переходы от одной допустимой угловой точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Рассмотрим симплекс метод на примере 2.7.1 задачи о фирме, выпускающей краску.

За начальную угловую точку возьмем точку О, от точки О осуществляется переход к смежной угловой точке. В нашем случае этой смежной точкой может быть либо точка Е, либо точка А.

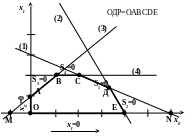
Рис. 19

Выбор точки (Е или А) зависит от коэффициентов целевой функции, которые определяют скорости ее прироста:

Так как в целевой функции коэффициент при х_Е больше коэффициента при х_I, а целевая функция подлежит максимизации, то требуемое направление перехода подлежит увеличению х_Е, что приводит к точке Е.

Далее анализируется можно ли еще увеличить f₀. Выбор каждой последующей экстремальной точки при использовании симплекс метода определяется двумя правилами.

Правило 1. Каждая последующая точка должна быть смежной с предыдущей, то есть невозможен в нашем примере прямой переход из точки О в вершину Д. Этот переход осуществляется по границам (ребрам) симплекса ОДР: от точки О к вершинам Е, из точки Е в точку Д.

Правило 2. Обратный переход к предшествующей вершине невозможен. Перед переходом от точки к следующей смежной вершине проверяется каждая текущая вершина на оптимальность.

Приведем задачу фирмы, выпускающей краски I и E к канонической форме.

Стандартная форма Каноническая форма

f0=3хE+2хI мах при ограничениях: х E+2хI  6 2хE+хI  8 хI -хE  1 хI  2 хI,хE 0

f0=3хE+2хI мах при ограничениях: х E+ 2хI + S1=6 2хE+хI + S2=8 хI -хE+ S3=1 хI + S4= 2 хI,хE0 Si0 i=

Каждую точку ОДР можно определить с помощью переменных х_Е, х_I, S₁,..., S₄, которые фигурируют в модели в канонической форме.

Для идентификации нужной вершины воспользуемся тем, что при S_i = 0, i = 1 ,.., 4 ограничения модели эквивалентны равенствам, которые представляются отрезками соответствующих прямых. При S₁ = 0 первое ограничение примет вид х_E+2х_I= 6 (ребро СD). Увеличение переменных S_i (S_i> 0; i=1,..,4) будет соответствовать смещению допустимых точек с границ ОДР в ее внутреннюю область.

Анализируя рис.19 можно определить каждую вершину ОДР через переменные:

Таблица 14

Вершины	Нулевые переменные	Ненулевые переменные
0	хE, хI	S1=6, S2=8, S3=1, S4=2
А	S3, хE	S1=4, S2=7, S4=1 хI=1
В	S3, S4	xI=2, хE=1, S1=1, S2=4
С	S1, S4	xI=2, хE=2, S2=2, S3=1
Д	S1, S2	xI= , хE= , S3=3, S4=
Е	хI, S2	xE=4, S1=2, S3=5, S4=2

Анализируя таблицу легко заметить две закономерности:

1. Стандартная модель содержит четыре уравнения (m = 4) и шесть неизвестных (n=6), поэтому в каждой из вершин две (6-4=2) переменных должны иметь нулевые значения.

2. Смежные вершины отличаются только одной переменной в каждой группе (нулевых и не нулевых переменных).

Первая закономерность говорит о возможности определения вершин алгебраическим путем приравнивания к нулю такого количества переменных, которые равны разности между количеством неизвестных и числом уравнений.

В этом состоит сущность свойства однозначности вершины, каждой вершине соответствуют две нулевых переменные; на ребре - одна нулевая переменная, внутри ОДР вообще не имеется ни одной нулевой переменной. Линейная модель содержит m уравнений (ограничений) и n неизвестных (n  m), причем правые части уравнений неотрицательны, тогда все допустимые вершины определяются как все однозначные неотрицательные решения системы m уравнений, в каждой вершине n-m переменных равны нулю. Однозначные решения такой системы уравнений, получаемых путем приравнивания к нулю (n-m) переменных, называются базисными.

Если базисное решение удовлетворяет требованию неотрицательности правых частей, оно называется допустимым базисным решением. Переменные, которые имеют нулевое значение, называются небазисными (свободными) переменными, а остальные базисными переменными (зависимыми переменными).

Максимальное число итераций при использовании симплекс - метода равно максимальному числу базисных решений задачи линейного программирования, то есть числу сочетаний из n по m:

Для рассмотренной задачи:

.

Вторая закономерность полезна при построении вычислительных процедур симплекс-методом, так как смежные вершины отличаются только одной переменной, которая определяет каждую последующую вершину (последующее базисное решение) путем замены одной из текущих нулевых не базисных переменных текущей базисной переменной.

Чтобы увеличить f₀ следует увеличить значение переменных х_Е от нуля, до значения х_Е в точке Е. При этом небазисная переменная х_Е переходит в разряд базисных, а соответствующая базисная переменная х₄ переходит в разряд небазисных. Таким образом, между множеством небазисных и базисных переменных происходит взаимообмен.

Вводимой в базис переменой называется небазисная переменная, которая будет включена во множество базисных переменных на следующей итерации. Исключаемая переменная - эта та базисная переменная, которая на следующей итерации (ходе) подлежит исключению из множества базисных переменных.