2.3.1 Формы представления задач линейного программирования

Существуют 3 формы записи задач ЛП. Рассмотрим их на примере 2.1.7.

1. Стандартная форма записи

Все ограничения записаны в виде неравенств, все переменные неотрицательны.

f =

при ограничениях:

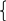
i=1,..,m

x_j 0 j=1,..,n

Запишем задачу в векторно-матричном виде

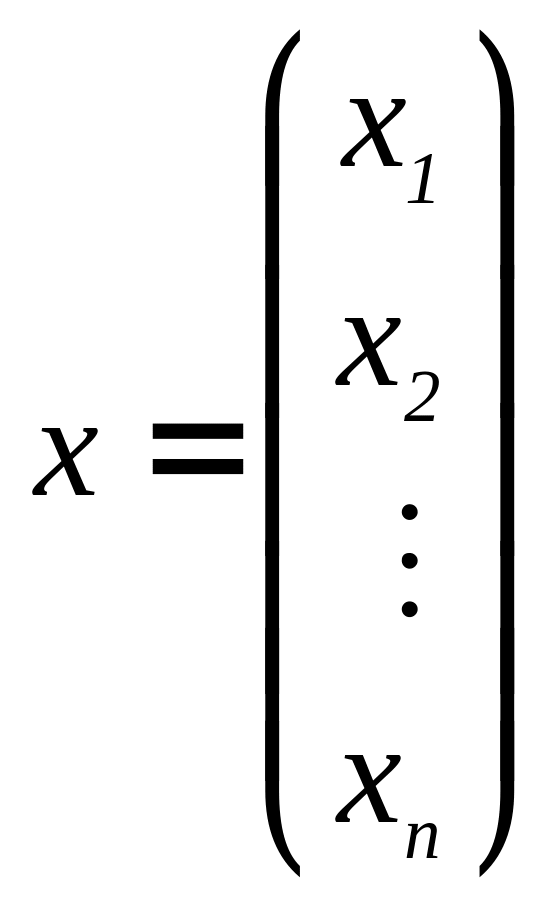
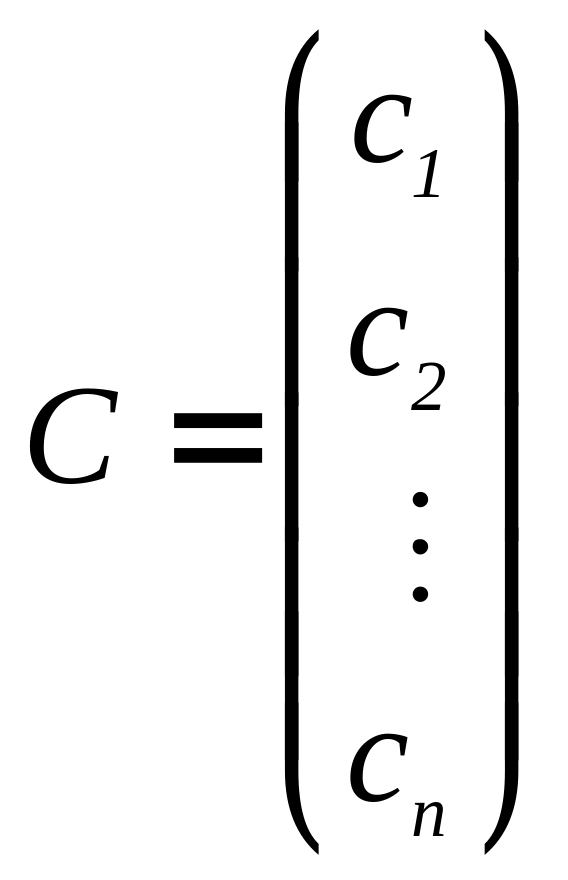
A=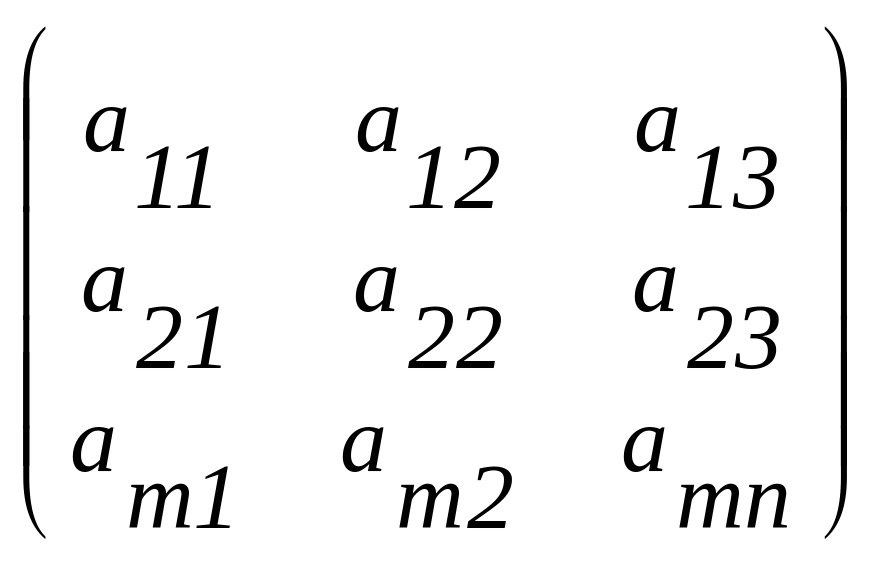

F=C, X max,

При ограничениях:

AX  B (2.5)

X  0 (2.6)

где < , >- скалярное произведение векторов.

2. Каноническая форма записи

Все ограничения заданы в виде равенства, все переменные неотрицательны.

при ограничениях:

i=1,..,m

x_j0 j=1,..,n

Все аналитические методы решения задач линейного программирования разработаны для канонической формы записи.

3. Общая форма записи

Часть ограничений задана в виде равенств, часть ограничений в виде неравенств, не все переменные будут неотрицательными, часть переменных неограниченна в знаке.

i=1,..,l

k=l+1,..,m

x_z 0 z=1,..,d

где d<n

Из одной формы записи задач ЛП путем несложного преобразования можно перейти в любую другую.

Например: задана задача в стандартной форме

при ограничениях:

i=1,..,m

x_j 0 j=1,..,n

Распишем ограничения:

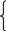a₁₁x₁+ a₁₂x₂+….+ a_1nx_n  b₁

a₂₁x₁+ a₂₂x₂+….+ a_2nx_n  b₂

a_m1x₁+ a_m1x₂+….+ a_mnx_n b_m

Введем дополнительные переменные такие, что:

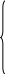x_n+1=b₁-

x_n+2=b₂-

…………………

x_n+m=b_m-

x_n+i 0 i=1,…,m

В результате ограничения получим в виде равенств:

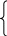a₁₁x₁+ a₁₂x₂+…+ a_1nx_n+ x_n+1=b₁

a₂₁x₁+ a₂₂x₂+…+ a_2nx_n +x_n+2=b₂

_{…………………………………………………………….}

a_m1x₁+ a_m1x₂+…+ a_mnx_n +x_n+m =b_m

Создаем расширенную матрицу условий А:

a11	a12		a1n	1	0	0
a21	a22		a2n	0	1	0
am1	am2		amn	0	0	1

Получаем задачу в канонической форме

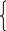F₀=<C, X> max

AX=B

X 0

Пусть вектор X^*=( x₁^*, x₂^*,….,x_n^*, x_n+1^*,…,x_n+m^* ) является решением задачи максимизации целевой функции F₀. Будем называть вектор Х* оптимальным планом.

Часть вектора X^*=( x₁^*, x₂^*,….,x_n^* ) является решением задачи в стандартной форме, при этом значения задач совпадают (значения целевых функций равны)

max F₀= max F

Рассмотрим преобразования, необходимые для перехода задачи из одной формы в другую.

Ограничение, заданное в виде равенства можно представить двумя ограничениями – неравенствами.

Н апример:

а₁₁x₁+а₁₂x₂+... +а_1n x_n=b₁ эквивалентно а₁₁x₁+а₁₂x₂+... +а_1n x_n  b₁

а₁₁x₁+а₁₂x₂+... +а_1n x_n  b₁

Чтобы перейти к однотипным неравенствам достаточно умножить левые и правые части на минус единицу, при этом знак неравенства изменяется на противоположный.

Если переменная x_z не ограничена в знаке, то ее можно заменить разностью 2-х положительных переменных

x_z=u - v, где u 0; v 0

при этом только одна переменная будет отлична от 0.

Пусть задана задача минимизации функции:

f =

на множестве Д, заданном ограничениями (2.5), (2.6). Пусть X^* - оптимальный план. Тогда из определения минимума функции должно выполняться неравенство

F(X^*)  F (X) (2.7)

для любых векторов X  Д.

Умножим неравенство (2.7) на минус единицу.

-F(X^*)  - F(X) (2.8)

Условие (2.8) является условием максимума функции, т.е. задача минимизации функции сводится к задаче максимизации противоположной функции:

min F = max (-F) (2.9)

При этом оптимальный вектор X^* один и тот же, а значения задач отличаются лишь знаком.