2Линейные математические модели

2.2.1Примеры постановок задач линейного программирования

Линейное программирование (ЛП, планирование) - это раздел исследования операций, в котором изучаются линейные оптимизационные модели (задачи поиска минимума затрат при условии выполнения необходимого объема работ или максимума прибыли при линейных ограничениях на ресурсы). Актуальность указанных критериев в современной экономической деятельности не вызывает сомнений.

Впервые постановка транспортной задачи ЛП дана в работе советского экономиста А. Н. Толстого (1930 г.). Советский ученый Л. В. Канторовичем (1939 г.) предложил общий метод решения задач ЛП (метод разрешающих множителей). Дж. Данцинг (США) в 1947 г. разработал симплекс - метод. Основоположником теории игр Дж. Нейманом в 1947 г. была развита концепция двойственности, что обеспечило увеличение практической ценности и расширение сферы применения методов ЛП. Л. В. Канторович совместно с М. К. Гавуриным в 1949 г. разработал метод потенциалов для решения транспортных задач. В настоящее время ЛП представляет собой высокоразвитый математический аппарат (теории, методы, алгоритмы и программы на ЭВМ).

Пример 2. 1. 1. Задача об ассортименте продукции

Фирма выпускает 3 вида изделий. В процессе производства используются три технологические операции. Технологическая схема производства изделий представлена на рис. 3.

В прямоугольниках указана длительность технологических операций при изготовлении изделий каждого вида. Для изделия 3 технологическая операция 3 не выполняется. Так как эти технологические операции используются фирмой и для других целей, то фонд рабочего времени, в течение которого операции могут быть применены для производства изделий, ограниченны следующими предельными значениями в сутки:

фонд рабочего времени

для первой операции - 430 мин.

для второй операции - 460 мин.

д ля третьей операции - 420 мин.

Рис. 3. Технологическая схема производства

Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия вида 1, 2 и 3 составляет 3, 2 и 5 долларов соответственно.

Найти оптимальный план производства изделий, максимизирующий суммарную прибыль.

Словесная формулировка цели (задачи)

Требуется определить суточные объемы производства изделий каждого вида (переменные модели), при которых максимизируется общая прибыль (целевая функция) при условии, что время использования каждой технологических операций в течение суток не превышает соответствующего предельного значения (ограничения).

Математическая модель задачи

Обозначим х_i ‑ количество изделий вида i (i = 1,2,3).

Функция цели: f₀ = 3х₁+ 2х₂+ 5х₃  mах

Найти оптимальные значения х_i (i=1,2,3) такие, что аргумент оптимизационной задачи х_i = arg max f₀ доставляет максимальное значение общей прибыли на множестве D:

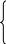1х₁+ 2х₂+ 1х₃430,

3х₁+ 2х₃460,

1х₁+ 4х₂420,

i  0, (i = 1, 2, 3).

Пример 2. 1. 2. Задача о составлении кормовой смеси

Бройлерное хозяйство птицефермы насчитывает 20000 цыплят, которых выращивают до 8-ми недельного возраста, после чего они поступают в продажу. Хотя недельный расход корма для цыплят зависит от их возраста, будем считать, что в среднем (за 8 недель) он составляет примерно 445г (1 фунт). Чтобы цыплята достигли к 8-й неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять требованиям по питательности. Этим требованиям могут соответствовать смеси различных кормов или ингредиентов (ограничимся тремя для примера). Будем в рационе для упрощения учитывать три вида питательных веществ.

Таблица 1

Ингредиенты	Содержание питательных веществ фунт/фунт			Стоимость $
	кальций	Белок	клетчатка
Известняк	0,38	Нет	нет	0,04
Зерно	0,001	0,09	0,02	0,15
Соевые бобы	0,002	0,5	0,08	0,4

Смесь должна содержать:

кальция не менее 0,8%, но более 1,2%,

белка - не менее 22%;

клетчатки - не более 5% от общего веса корма.

Словесная формулировка задачи

Требуется определить количество (в фунтах) каждого из трех ингредиентов (переменные), образующих смесь минимальной стоимости (целевая функция) при соблюдении требований к общему расходу кормовой смеси и ее питательности (ограничения).

Математическая модель задачи

Введем обозначения: х₁-содержание известняка, х₂-содержание зерна, х₃-содержание соевых бобов (в фунтах) в смеси.

Минимальный общий вес смеси, еженедельно расходуемый на кормление 20000 цыплят: 200001=20000 фунтов.

Так как х₁,х₂,х₃ - представляют собой вес трех ингредиентов в смеси, то общий вес смеси равен х₁+х₂+х₃. Причем эта сумма не должна быть меньше 20000 фунтов, то есть х₁+ х₂+х₃ 20000

Обратим внимание на требование по питательности. Содержание кальция должно находиться в пределах 0,008 умноженное на количество фунтов, то есть от 0,008(x₁+ х₂+ х₃) до 0,012(х₁+х₂+х₃). В соответствии с таблицей содержание кальция, обусловленное включением в смесь х₁ фунтов известняка, х₂ фунтов зерна и х₃ фунтов соевых бобов равны 0,38х₁+ 0,001х₂+0,002х₃.

Тогда ограничения, связанные с содержанием кальция в кормовом рационе может быть представлено в следующем виде:

0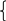 ,38х₁ + 0, 001х₂ +0,002х₃  0,008(х₁+х₂+х₃)

0,38х₁+0,001х₂+0,002х₃ 0,012(х₁+х₂+х₃)

П риведем подобные:

0,372х₁-0, 007х₂-0,006х₃ 0

0,368х₁-0, 011х₂-0,01х₃ 0

Аналогично составляются ограничения по норме белка в корме

0,09х₂ + 0,5х₃  0, 22(х₁ + х₂ + х₃)

или

0,22x₁ + 0,13х₂-0, 28х₃ 0

По содержанию клетчатки

0,02х₂ + 0,08х₃  0,05(х₁+х₂+ х₃)

или

0,05x₁ + 0,03х₂ –0,03х₃ 0

Окончательно математическая модель задачи имеет вид:

f = 0, 04х₁+ 0,15х₂+0,4х₃ = min

при ограничениях:

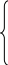х₁+ х₂+ х₃  20000 (минимальный недельный рацион)

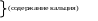0,372х₁-0,007х₂-0,006х₃  0

0,368х₁-0,011х₂-0,01х₃  0

0,22х₁ +0,13х₂-0,28х₃ 0 (содержание белка)

0,05х₁+ 0,03х₂-0,03х₃  0 (содержание клетчатки)

х_j  0 для j=1, 2, 3.

Пример 2. 1. 3. Сменно - суточное планирование работы автобусного парка

Исследуется возможность более рациональной организации работы городского автобусного парка с целью снижения интенсивности городского движения. Сбор и обработка необходимой информации позволяет сделать вывод, что минимальное количество автобусов на линии, удовлетворяющее потребности в перевозках, существенно меняется в течение суток. Оказалось, что требуемое количество автобусов можно считать величиной постоянной в пределах каждого из следующих друг за другом четырех интервалов времени t (рис. 4).

C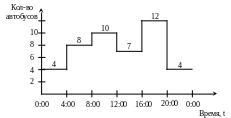 учетом необходимых затрат времени на текущий ремонт и обслуживание непрерывное использование автобусов на линии должно продолжаться по 8 часов в сутки.

Рис. 4. Требуемое количество автобусов в течение суток

Словесная формулировка задачи

Требуется определить количество автобусов в каждой из смен (переменные), которое должно быть не меньше минимальной потребности в них (ограничения) при условии, что общее количество автобусов, выходящих на линию в течение суток, будет минимальным (целевая функция).

Математическая формулировка задачи

Известно, что продолжительность смены 8 часов, однако неизвестно, когда должна начинаться та или иная смена. Если ориентироваться на общепринятый трехсменный график работы (8:01-16:00), (16:01-24:00), (24:01-8:00) и обозначить количество автобусов, выходящих на линию в 1, 2 и 3 смены через х₁, х₂, х₃ соответственно, то из рис. 4 видно, что х₁10; х₂12; х₃8, поэтому общее минимальное количество используемых автобусов равно: х₁+ х₂+ х₃ = 10 + 12 + 8 = 30.

Однако может оказаться, что выгоднее график работы, составленный на основе оптимального выбора начала каждой из смен. Можно использовать, например, график работы, в котором начало одной смены смещено относительно начала следующей смены на 4 часа. Такой график с непрерывающимися сменами показан на рис.5, причем продолжительность смены составляет 8 часов. Тогда следует ввести следующие переменные:

х₁ - число автобусов, выходящих на линию в 0:01 час, х₂ - в 4:01 час, х₃ - в 8:01 час, х₄ - в 12:01 час, х₅ - в 16:01 час, х₆ - в 20:01 час.

20:00

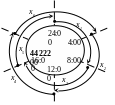
Рис.5. График работы автобусов

Математическая модель задачи

f₀=x₁+х₂+х₃+х₄+х₅+х₆= min

при ограничениях:

х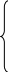 ₆+х₁ 4 (с 0:01 до 4:00)

х₁+х₂ 8 (с 4:01 до 8:00)

х₂+х₃ 10 (с 8:01 до 12:00)

х₃+х₄ 7 (с 12:01 до 16:00)

х₄+х₅ 12 (с 16:01 до 20:00)

х₅+х₆ 4 (с 20:01 до 24:00)

х_j 0 для j = 1, 2,..,6, х_j – целые.

Пример 2.1.4. Задача о раскрое или минимизации обрезков

Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины - по 20 дм. По специальным заказам потребителей фирма поставляет рулоны нестандартных размеров. Типичные заказы на рулоны нестандартных размеров приведены в таблице.

Таблица 2

Заказ	Требуемая ширина, дм.	Требуемое количество рулонов, шт.
1	5	150
2	7	200
3	9	300

Словесная формулировка задачи

Требуется найти сочетание вариантов установки режущей кромки (переменные), при которых поступившие заказы (ограничения) удовлетворяются с минимальными потерями (целевая функция).

Математическая формулировка задачи

Определение переменных, необходимо видоизменить таким образом, чтобы оптимальным решением мог воспользоваться оператор, управляющий работой режущего устройства. Переменные следует определять как х_j - количество стандартных рулонов, которые должны быть разрезаны по j-му варианту раскроя. (j=1,2,..,6)

Таблица 3

Требуемая ширина, дм	Варианты раскроя рулона						Min количество рулонов
	1	2	3	4	5	6
5	0	2	2	4	1	0	150
7	1	1	0	0	2	0	200
9	1	0	1	0	0	2	300
Ширина рулона-обрезка, дм	4	3	1	0	1	2

Потери будем оценивать по площади бумаги в рулонах – обрезках и в лишних рулонах шириной 5, 7, 9 дм. Допустим, что длина каждого рулона одинакова и равна L.

Обозначим: y₁ - количество лишних рулонов шириной 5 дм,

y₂ - количество лишних рулонов шириной 7 дм,

y₃ - количество лишних рулонов шириной 9 дм.

Математическая модель задачи:

f =L (4x₁+3x₂+x₃+x₅+2x₆ )+L (5y₁+7y₂+9y₃ ) min

при ограничениях:

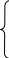2x₂+2x₃+4x₄+x₅ 150

х₁+ x₂+2x₅ 200

x₁+x₃+2x₆ 300

x_j 0 j=1,2,..,6,

y_i 0 i=1,2,3

х_j,y_i - целые

Так как L=const, поэтому этот параметр можно не учитывать в целевой функции, кроме того, учтем, что

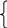y₁= 2x₂+2x₃+4x₄+x₅ -150

y₂= х₁+ x₂+2x₅ -200

y₃= x₁+x₃+2x₆ –300,

тогда f=4x₁+3x₂+x₃+x₅+2x₆+5y₁+7y₂+9y₃ min

при ограничениях:

2 x₂+2x₃+4x₄+x₅ -y₁=150

x₁+x₂+2x₅ - y₂=200

x₁+x₃+2x₆ -y₃=300

x_i, y_j 0 j=1,2,3; i=1,2,..,6 х_j,y_i - целые

Пример 2.1.5. Задача минимизации дисбаланса на линии сборки

Словесная формулировка задачи

Фирма изготовляет изделия, состоящие из узлов вида 1, вида 2 и вида 3.

Таблица 4

Завод	Ресурсы времени в нед., час	Производительность узел/час
		Узел 1	Узел 2	Узел 3
1	100	8 (x11)	12 (x12)	5 (x13)
2	80	6 (x21)	14 (x22)	4 (x23)

Требуется определить ресурсы времени на производство узлов каждого вида на каждом заводе, не превышающих ресурсы времени каждого завода и максимизирующие количество выпускаемых изделий.

Математическая формулировка задачи

Обозначим: х_ij - время, в течение которого на i–ом заводе изготавливается узел вида j.

Тогда количество узлов 1-го вида 8х₁₁+6х₂₁;

узлов 2-го вида 12х₁₂+14х₂₂;

узлов 3-го вида 5х₁₃+4х₂₃.

Число изделий будет совпадать с минимальным количеством узлов, какого – либо вида.

Целевая функция:

f=min (8x₁₁+6x₂₁; 12x₁₂+14x₂₂; 5x₁₃+4x₂₃) mах

при ограничениях:

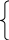x₁₁+x₁₂+x₁₃ 100

x₂₁+x₂₂+x₂₃ 80

x_ij 0,

i=1,2; j=1,..,3

В такой постановке целевая функция не является линейной. Введем новую переменную:

у= min(8x₁₁+6x₂₁; 12x₁₂+14x₂₂; 5x₁₃+4x₂₃) ,

Тогда f= y max

при ограничениях:

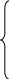x₁₁+x₁₂+x₁₃ 100

x₂₁+x₂₂+x₂₃ 80

8x₁₁+6x₂₁ у

12x₁₂+14x₂₂ у

5x₁₃+4x₂₃ у

x_ij 0, у_i 0,

i=1,2; j=1,2,3;

y_i- целые

Пример 2.1.6. Целевое программирование

При построении моделей, адекватных реальным ситуациям, необходимо отразить тот факт, что при соответствующей компенсации (штрафе) можно допустить нарушение того или иного ограничения. Такой вид планирования называется целевым.

Словесная формулировка задачи

Станки могут работать в течение 8 часов в сутки, но время работы станка может быть увеличено за счет сверхурочных работ не более чем на 4 часа в сутки. Каждый час сверхурочной работы требует дополнительных расходов 5$ в расчете на одно изделие. Требуется определить объем производства изделий каждого вида из условия максимизации чистой прибыли.

Таблица 5

Станок	Производительность, изд/час
	Изделие 1	Изделие 2
1	5	6
2	4	8
Прибыль $	6	4

Обозначим:

x₁ - количество изделий вида 1

x₂- количество изделий вида 2

у₁ - сверхурочное время работы на станке 1

у₂ - сверхурочное время работы на станке 2

Если y_i<0, то сверхурочные не нужны и станок i работает меньше 8 часов в сутки.

Математическая модель задачи

f=6x₁+4x₂-5 max(0;y₁)-5 max(0;y₂) mах

При ограничениях:

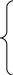
y₁ 4 y₂ 4

x_i 0 , i=1, 2

у_j не ограничены в знаке

x_i - целые

Так как целевая функция нелинейная, то переходим к линейной, вводя новые переменные:

z₁=max(0;y₁); z₂=max(0;y₂).

С введением z₁ и z₂ появятся два ограничения: z₁ y₁ и z₂ y₂. Теперь математическая модель является линейной:

f=6x₁+4x₂-5(z₁+z₂) max

при ограничениях:

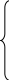
y_i 4

z_i-y_i 0

z_i 0

x_i 0 , i=1,2

у_j не ограничены в знаке i=1,2

Пример 2.1.7. Задача об оптимальном планировании производства

Сформулируем задачу в общем виде. Предприятие при изготовлении n видов изделий в количествах х_j единиц (j=1,..,n) использует m видов ресурсов.

Запасы b_i (i=1,..,m) каждого ресурса заданы. Известны нормы а_ij расхода i–го ресурса на производство единицы изделия вида j, прибыль с_j от продажи одного изделия вида j. Требуется определить оптимальный план производства изделий X^*=(х₁, х₂,..,х_n), максимизирующий суммарную прибыль.

Математическая модель

f = c₁x₁+ c₂x₂+...+ c_nx_n=

при ограничениях на расход ресурсов:

а ₁₁_x₁+a₁₂x₂+... +a_1n_x_n  b₁

а₂₁_x₁+a₂₂_x₂+... +a_2n_x_n  b₂

_{…………………………………………….} (2.1)

а_m1_x₁+a_m2_x₂+... +a_mn_x_n  b_m

x_j 0 j=1, 2,.., n

Систему (2.7) можно записать более компактно:

Пример 2. 1. 8. Задача об оптимальной загрузке оборудования

Предприятию необходимо выполнить производственный заказ на имеющемся оборудовании. Для каждой единицы оборудования заданы: фонд рабочего времени, себестоимость на изготовление единицы продукции каждого вида и производительность, т.е. число единиц продукции каждого вида, которое можно произвести в единицу времени. Нужно распределить изготовление продукции между оборудованием таким образом, чтобы себестоимость продукции была минимальна.

Математическая формулировка задачи

Целью является минимизация себестоимости.

Параметры:

m - номенклатура, т.е. число различных видов продукции в производственном заказе;

b_i - число единиц продукции i-го вида, i=1,..,m;

n - число единиц оборудования;

T_j - фонд времени работы оборудования j-го типа, j=1,..,n;

a_ij - производительность оборудования j-го типа по производству изделий i-го вида, j=1,..,n; i=1,..,m;

C_ij - себестоимость изготовления единицы продукции i-го вида на оборудовании j-го типа, i=1,..,m; j=1,..,n;

Управляющие переменные x_ij, (i=1,. . . , m; j=1, . . ,n) - это время, в течение которого оборудование j-го типа занято изготовлением продукции i-го вида. Критерий оптимальности задается функцией:

С= min

где С – суммарная себестоимость.

Область допустимых решений определяется ограничениями (2.2) по фонду времени, ограничениями (2.3) по номенклатуре и условиями неотрицательности x_ij (2.4).

x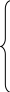 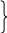₁₁+x₂₁+…+x_m1 T₁

x

(2.2)

₁₂+x₂₂+…+x_m2 T₂

…………………………

x_1n+x_2n+…+x_mn T_n;

a

(2.3)

₁₁x₁₁+a₁₂x₁₂+…+a_1nx_1n=b₁; a₂₁x₂₁+a₂₂x₂₂+…+a_2nx_2n=b₂;

……………………………………

a_m1x_m1+a_m2x_m2+…+a_mnx_mn=b_m;

x

(2.4)

_ij 0,

i=1,. . . .,m, j=1,. . . ,n

Пример 2. 1. 9. Выбор портфеля ценных бумаг

При инвестировании денежных средств в ценные бумаги: акции, облигации, валюты, вексели, возникают задачи оптимизации. Обычно денежные средства вкладывают в несколько видов ценных бумаг, которые образуют портфель активов.

Доходность портфеля характеризуется средневзвешенной доходностью его составляющих, которая для портфеля из двух активов рассчитывается следующим образом:

Д=W_а Д_а+W_bД_b;

где Д – общая доходность портфеля;

W_а – удельный вес актива А;

Д_а – доходность актива А;

W_b – удельный вес актива В;

Д_b – доходность актива В.

Будущая стоимость ценных бумаг (в отличие от текущей) не определена, зависит от большого количества различных факторов. Количественная мера этой неопределенности называется риском. При этом методы линейного программирования можно использовать для контроля систематического риска при формировании портфеля активов.

Допустим, имеется множество активов A_i ( ), а ожидаемые доходы от них соответственно равны Д_i. Доли каждого из этих активов в портфеле соответственно равны W_i и являются переменными, которые могут корректироваться. Риск портфеля R определяется как средневзвешенная величина рисков активов r_i.

Цель процедуры оптимизации заключается в максимизации дохода по портфелю при заданном ограничении уровня риска портфеля.

Математическая формулировка задачи

Определим оптимальные пропорции (веса) каждого из активов, которые приведут к максимальному ожидаемому дохожу при условии заданного максимального уровня риска. Эта задача может быть сформулирована следующим образом.

Ограничения связаны с тем, что:

1. Риск R портфеля не должен превышать R_доп;

2. В каждый актив обязательно должны быть проведены положительные инвестиции;

3. Все средства должны быть полностью инвестированы.

Таким образом, ограничения имеют следующий вид:

,

где все активы могут иметь только неотрицательные веса

;

причем ;

поскольку средства должны быть полностью инвестированы.

Все ограничения линейны и представлены в виде равенств и неравенств. Целевая функция имеет вид:

Поскольку доход по каждому активу предопределен, то только веса могут быть изменяемы в целевой функции.