Поверхности Безье: Построение [Construction]

Поверхность Безье определяется двумерным набором контр. точек p_i,j, где i в пределах от 0 до m, а j в пределах от 0 до n. Таким образом, в этом случае, имеем m+1 рядов и n+1 столбцов контр. точек и контр. точка в i-м ряду и j-м столбце обозначается p_i,j. Заметьте, в итоге получается (m+1)(n+1) контр. точек.

Вот уравнение поверхности Безье, определяемой m+1 рядами и n+1 столбцами контр. точек:

,

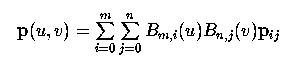где B_m,i(u) и B_n,j(v) - это i-ая и j-я базисные функции Безье в направлениях u и v, соответственно. Как вы помните из обсуждения кривых Безье, эти базисные функции определяются так:

Так как B_m,i(u) и B_n,j(v) - функции степеней m и n, то можно сказать, что это поверхность Безье степени (m,n). Набор контр. точек обычно называют сеткой Безье или контрольной сеткой. Заметьте, что параметры u и v в пределах от 0 до 1 и поэтому для поверхности Безье квадратная часть сетки проецируется на прямоугольный участок поверхности.

Следующий рисунок показывает поверхность Безье, определяемую 3 рядами и 3 столбцами (т.е. девятью) контр. точками и поэтому являющуюся поверхностью степени (2,2).

Базисные Функции

Базисные функции поверхности Безье - это коэффициенты контр. точек. Из определения ясно, что эти двумерные базисные функции - это произведение двух одномерных базисных функций Безье и поэтому базисные функции Безье являются параметрическими поверхностями с двумя переменными u и v, определенными на квадратной области. Следующие рисунки показывают базисные функции для контр. точек p_0,0 (слева) и p_1,1 (справа), соответственно. Для контр. точки p_0,0, ее базисная функция равна произведению двух одномерных базисных функций Безье B_2,0(u) в направлении u и B_2,0(v) в направлении v. На рисунке слева, и B_2,0(u), и B_2,0(v) показаны вместе с их произведением(показано сеткой). На рисунке справа показана базисная функция для p_1,1, являющегося произведением B_2,1(u) в направлении u и B_2,1(v) в направлении v.

Поверхности [Tensor] Произведения

С помощью техники [tensor] произведения поверхность образуется "произведением" двух кривых. Даны две кривых Безье, B-spline или NURBS; метод [tensor] произведения дает поверхность при помощи произведения базисных функций первой кривой и базисных функций второй, т.е. используем результат в качестве базисных функций для двумерного набора контр. точек. Поверхности, полученные таким образом, называются поверхностями [tensor] произведения. аким образом, кривые Безье, B-spline и NURBS - это все поверхности [tensor] произведения

Поверхности Безье: Важные Свойства

Здесь перечисляются некоторые важные свойства поверхностей Безье. Эти свойства можно легко проверить, используя те же методы, что и для кривых Безье. Пожалуйста, сравните эти важные свойства со свойствами кривых Безье. Вспомним уравнение поверхности Безье:

,

где двумерные базисные функции определяются так:

• p(u,v) проходит через контр. точки в четырех углах контрольной сетки: p_0,0, p_m,0, p_m,n и p_0,n. Фактически, имеем p(0,0) = p_0,0, p(1,0) = p_m,0, p(0,1) = p_0,n и p(1,1) = p_m,n.

• Неотрицательность: B_m,i(u) B_n,j(v) неотрицательно для всех m, n, i, j и u и v в пределах от 0 до 1. Это очевидно.

• Деление Единства: Сумма всех B_m,i(u) B_n,j(v) равна 1 для всех u и v в пределах от 0 до 1. Говоря точнее, это значит, что для любой пары u и v в пределах от 0 до 1, выполняется следующее:

• Свойство Огранич. Многоугольника (многогранника?) : поверхность Безье p(u,v) лежит внутри ограничивающего многоугольника ее контр. сетки. Так как p(u,v) - это линейная комбинация всех ее контр. точек с положительными коэффициентами, сумма которых равна 1 (деление единства), то поверхность лежит внутри огранич. многоугольника ее контр. точек.

• Инвариантность при Подобных [affine] Преобразованиях Это значит то же самое, что и для кривых...

• Свойство Уменьшения Изменчивости: Ничего такого для поверхностей не работает. [No such thing exists for surfaces.]