Соотношение Между Производной и Алгоритмом de Casteljau

Перепишем производную кривой Безье, разбив последний член p_i+1-p_i на два:

Таким образом, производная кривой Безье - это разность двух кривых Безье степени n-1. Для простоты, пусть эти кривые будут C₁(u) и C₂(u):

Из этих определений получаем, что первая кривая C₁(u) описывается контрольными точками p₁, p₂, ..., p_n, а вторая кривая C₂(u) описывается контрольными точками p₀, p₁, ..., p_n-1. Производная равна:

Таким образом, теоретически, для того, чтобы вычислить производную p(u) для отдельного u, можно использовать алгоритм de Casteljau, чтобы вычислить C₁(u) и C₂(u). Затем, вычислив их разность и умножив на n, получим p'(u).

Теперь надо использовать алгоритм de Casteljau. Посмотрите на рисунок ниже. В левом столбце находятся все данные контрольные точки. Точка n0 дает точку p(u) на кривой, а отрезок, соединяющий (n-1)0 и (n-1)1 - это последняя ломаная в алгоритме de Casteljau. Фактически, n0 лежит на отрезке от (n-1)0 до (n-1)1, причем отношение расстояний между (n-1)0 и n0, и между (n-1)0 и (n-1)1 равно u.

Так как кривая C₁(u) описывается контрольными точками 01, 02, ..., 0n, то, используя диаграмму (выше), можно видеть, что (n-1)1 - это точка на кривой C₁(u). Соответственно, так как C₂(u) описывается контрольными точками 00, 01, ..., 0(n-1), видно, что (n-1)0 - это точка на кривой C₂(u). Таким образом, вектор C₁(u)-C₂(u) - это вектор от точки (n-1)0 до точки (n-1)1, а производная p(u) равна C₁(u)-C₂(u), умноженному на n.

Что из этого следует? Так как ломаная от (n-1)0 до (n-1)1 в алгоритме de Casteljau имеет то же направление, что и касательный вектор в точке p(u), она касательна кривой в p(u)! В итоге получаем, что

Последняя кривая, т.е. отрезок, в алгоритме de Casteljau, касательна кривой Безье в точке p(u).

Пример на следующем рисунке поясняет это. Показана точка, для которой u = 0.5. Видно, что последний отрезок в сети de Casteljau касателен кривой в p(0.5).

Производные Высших Порядков [Higher Derivatives]

Вычисление производных высших порядков кривых Безье - дело несложное. Вспомним, что производная p(u) - это

Применяя формулу производной к этой кривой Безье, получим следующее, т.е. вторую производную исходной кривой:

Найдя p'(u) и p''(u), можно будет очень легко найти направляющую тройку веторов и кривизну в точке p(u). Производные высших порядков можно находить, рекурсивно применяя формулу производной.

Чтобы подробнее рассмотреть производные высших порядков, нужно ввести понятие конечной разности. Пусть конечная разность нулевого уровня D_i⁰ описывается контрольными точками P_i для 0 <= i <= n. Затем, конечная разность первого уровня D_i¹ - это разность между элементами предыдущего уровня, т.е. нулевого (D_i⁰):

Заметьте, что в разности первого уровня только n точек, на одну меньше, чем количество исходных контрольных точек. Еще точнее, первый уровень разности - это

Второй уровень разности описывается разностью точек первого уровня.

Второй уровень разности имеет n-1 точек. Повторяя эту процедуру, можно получить k-й уровень разности (см. ниже). В k-ом уровне разности n-k+1 точек.

С помощью такого обозначения можно описать производную довольно коротко. Прежде всего, перепишем p'(u) используя разности D_i¹:

Вычисляя производную p'(u), чтобы получить p''(u), получим формулу p''(u) с участием D_i²:

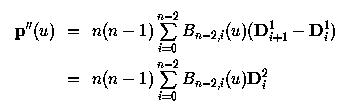
Сделав то же самое с p''(u), получим формулу p'''(u) через D_i³:

Продолжая в том же духе, можно получить k-ю производную p^[k](u) через D_i^k:

Таким образом, чтобы вычислить k-ю производную p(u) для конкретного u, можно сначала вычислить разности D_i^k и применить алгоритм de Casteljau для нахождения точки, соответствующей u на кривой Безье, описываемой точками D_i^k. Говоря точнее, можно сгруппировать все D_i⁰ в нулевой столбец, назначить стрелкам знаки (вверх (красные) +, вниз (синие) - ) для вычисления столбца 1 разностей D_i¹. Повторяем эту операцию до тех пор, пока не дойдем до столбца k, как показано ниже:

В конце концов, применив алгоритм de Casteljau к точкам столбца k при данном u, получим вектор p^[k](u)!