Разбиение Кривой Безье

Значение разбиения в разделении данной кривой Безье в p(u) для некоторого u на два отрезка кривой, каждый из которых также является кривой Безье. Из-за того, что полученные кривые должны иметь свои собственные наборы контрольных точек, исходный набор точек отбрасывается. Кроме того, так как исходная кривая Безье степени n разделяется на две части, каждая из которых является подмножеством исходной кривой n степени, результирующие кривые Безье также должны быть степени n.

Наша задача:

Дан набор n + 1 контрольных точек p₀, p₁, p₂, ..., p_n и значение параметра u в пределах от 0 до 1, нужно найти два набора по n+1 контрольных точек q₀, q₁, q₂, ..., q_n и r₀, r₁, r₂, ..., r_n, чтобы кривая Безье, построенная по точкам q_i (соотв., r_i) была частью исходной кривой Безье на [0,u] (соотв., [u,1]).

Хоть проверка корректности и немного скучна, но сам алгоритм очень прост. Фактически, алгоритм de Casteljau для определения точки p(u) на кривой дает всю необходимую информацию. На рисунке снизу слева, показаны все промежуточные шаги при использовании этого алгоритма, а на рисунке справа показано разбиение кривой на две части в точке p(u), а также соотв. этим частям ломаные контрольных точек.

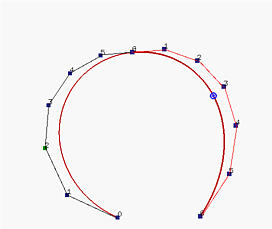
Если вы хорошо сравните эти два рисунка, вы, вероятно, заметите, что ломаная слева состоит из точек p₀₀ = p₀, p₁₀, p₂₀, p₃₀, p₄₀, p₅₀ и p₆₀ = p(u), а кривая справа - из точек p₆₀ = p(u), p₅₁, p₄₂, p₃₃, p₂₄, p₁₅ и p₀₆ = p₆. Следующие рисунки иллюстрируют выбор этих точек.

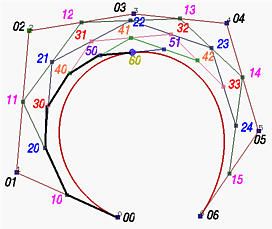
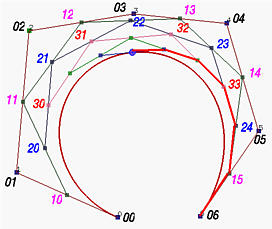
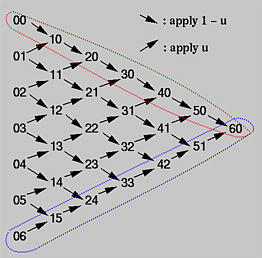
Вспомните о треугольной схеме вычисления по алгоритму de Casteljau. Для данного u нужно n итераций, чтобы вычислить p(u). По ходу вычислений, берем первую и последнюю точки в каждом столбце, а в конце набор всех первых (соотв., последних) точек даст ту часть разделения исходной кривой, которая лежит на отрезке [0,u] (соотв., на [u,1]). Таким образом, в следующей треугольной схеме, двигаясь от верхнего угла по направлению стрелок, а затем от вершины против направления стрелок к нижнему углу, получим два набора точек для двух соответствующих отрезков разделения.

Заметьте, что так как отрезок, соединяющий точки 50 и 51, касателен кривой в точке 60, то и последний сегмент левой кривой (т.e., между точками 50 и 60) касателен левой кривой, а первый сегмент правой кривой (т.e., между точками 60 и 51) соответственно касателен правой.

Зачем Это Нужно, блин ? [Why Do We Need Curve Subdivision?]

Э, не скажи. Тут великая польза 8-). Например, можно использовать ее для нахождения пересечения кривых Безье, их расчета, для упрощения разработки кривых. Допустим, у нас есть кривая, но она нам не очень подходит. В этом случае можно разделить ее на две части в нужной точке, на подходящую и неподходящую. Затем, можно забыть о нормальной части и сосредоточиться на "кривой".

Можно применять разделение кривой сколько угодно раз. Но нужно помнить, что, если мы хотим сохранить гладкость перехода, нужно, чтобы отрезки в точке соединения были коллинеарны.

Повышение Степени Кривой Безье

Во многих случаях при работе с кривыми Безье нужно, чтобы они были одинаковых степеней. Кроме того, хотя кривые Безье высших степеней труднее рассчитывать, они все же являются более гибкими при разработке. Поэтому может быть очень полезным увеличение степени кривой Безье без изменения ее формы. Заметьте, что "без изменения формы кривой" является ключевым пунктом; иначе увеличение степени не принесет никакой практической пользы. Увеличение степени кривой Безье без изменения ее формы называется повышением степени. Далее мы обсудим только алгоритм.

Допустим, дана кривая Безье степени n, определяемая n + 1 контрольными точками p₀, p₁, p₂, ..., p_n и нам надо увеличить степень этой кривой до n + 1 без изменения ее формы. Так как кривая Безье степени n + 1 определяется n + 2 контрольными точками, нам необходимо найти этот новый набор точек. Очевидно, p₀ и p_n должны быть в новом наборе точек, потому что кривая проходит через них. Таким образом, нам нужно только n новых контрольных точек. Пусть новый набор контрольных точек будет q₀, q₁, q₂, ..., q_n+1. Как упоминалось ранее, q₀ = p₀ и q_n+1 = p_n. Другие контрольные точки рассчитываются так:

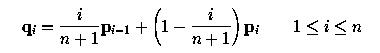
Если вас не устраивает такая общая формула, вот вам формулы для каждой контрольной точки от q₁ до q_n.

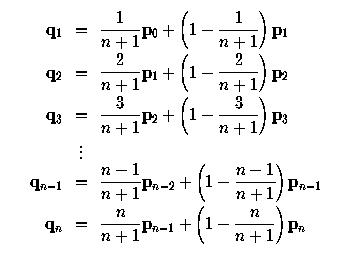
Каждый сегмент исходной ломаной содержит точно одну новую контрольную точку. Говоря точнее, сегмент p_i-1p_i содержит новую контрольную точку q_i. Вспомним из обсуждения алгоритма de Casteljau, что точку C на отрезке прямой между точками A и B, причем отношение расстояний между A и C и между A и B равно u, можно записать в виде C = (1 - u)A + uB. Из формул для новых контрольных точек видно, что отношение расстояний между p_i-1 и q_i и между p_i-1 и p_i равно 1 - i/(n+1). Тем не менее, в отличие от алгоритма de Casteljau, это соотношение не постоянно, а варьируется в зависимости от i. Но все же вычисления очень похожи на алгоритм de Casteljau.

Получив новый набор точек, исходный можно отбросить. Так как каждый сегмент исходной ломаной содержит новую контрольную точку, процесс получения новой ломаной похож на обрезание углов у исходных контрольных точек. Это показано на следующем рисунке. Рисунок показывает повышение степени с 4 до 5, новая ломаная показана темными линиями, старая - светлыми. В таблице слева указаны соотношения, по которым получаются точки новой ломаной.

i	1 - i/(n+1)
1	0.8
2	0.6
3	0.4
4	0.2

Заметьте, что повышение степени можно проводить последовательно сколько угодно раз, пока ваша система это сможет делать. Заметьте также, что с увеличением степени растет и количество контрольных точек. Кроме того, контрольная ломаная приближается к кривой.

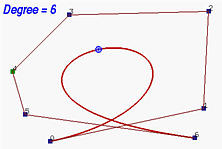
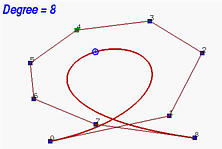
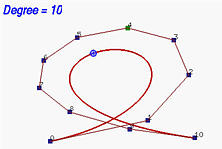
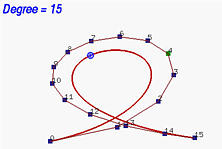
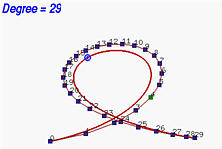
На следующих рисунках, начиная с кривой 6 степени, степень повышалась до 7, 8, 10, 15 и, в итоге, 29. Видно, что форма кривой оставалась неизменной, а ломаная все ближе и ближе пдоходила к кривой. При увеличении степени до бесконечности, ломаная сливается с кривой - ее предельным положением.

B-spline: Мотивация

Допустим, нам нужно спроектировать профиль вазы. Рисунок слева - это кривая Безье 11 степени; но все-же сложно сделать так, чтобы "шея" огибала отрезок p₄p₅. Конечно, можно добавить контрольных точек около этого отрезка, чтобы увеличить вес в этой области. Но тогда увеличится степень кривой. Во многих случаях невыгодно использовать кривые высших степеней.

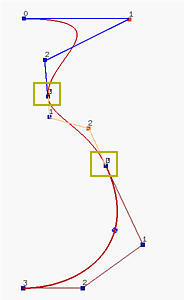
Как оговаривалось на предыдущей странице о производных кривых Безье, мы можем объединить две кривых Безье. Если последний сегмент ломаной первой кривой и первый сегмент ломаной второй кривой лежат на одной прямой, получаем по крайней мере G¹-непрерывность, так как касательные векторы направлены в одну сторону (т.e., если их длины равны, получаем непрерывность C¹). Рисунок посередине показывает это. На нем три отрезка кривых Безье, точки соединения показаны в желтых прямоугольниках. Мы видим, что с помощью нескольких кривых Безье меньших степеней, удовлетворяющих условию "коллинеарности", можно получить необходимую сложную форму. Но поддержание этой "коллинеарности" может быть довольно утомительным и нежелательным.

Возможно ли использовать отрезки кривых младших степеней, не заботясь об этом условии "коллинеарности" ? Кривые B-spline - это обобщение кривых Безье, разработанные для такого случая. На правом рисунке изображена кривая B-spline третьей степени с 8-ю контрольными точками. Фактически, это - пять кривых Безье 3-й степени, вместе образующих кривую B-spline, определяемую контрольными точками. Маленькие точки делят кривую на отрезки. Можно перемещать контрольные точки, чтобы изменить форму кривой, также, как и с кривыми Безье. Также можно изменять деление кривой. Таким образом, кривые B-spline имеют большую степень свободы в проектировании кривых.

Деление кривой напрямую довольно сложно. Вместо этого мы можем разделить диапазон кривой. То есть, если область кривой - это [0,1], то этот закрытый диапазон разделяется точками, называемыми узлами. Пусть узлы будут 0 <= u₀ <= u₁ <= ... <= u_m <= 1. Тогда точки p(u_i) делят кривую, как показано на рисунке ниже, и, следовательно, изменение деления отрезка [0,1] изменяет форму кривой.

В итоге, чтобы создать кривую B-spline, нам нужны: набор контрольных точек, набор узлов и набор коэффициентов, по одному на каждую контрольную точку, т.е. чтобы все отрезки кривой соединялись и выполненялось нужное условие непрерывности. Вычисление коэффициентов - это, возможно, самая сложная часть работы, так как они должны гарантировать выполнение определенных условий непрерывности. К счастью, эти вычисления в этом курсе не понадобятся. Нам лишь нужно знать их характеристики для рассуждения о кривых B-spline.