Нахождение точки на Кривой Безье: Алгоритм De Casteljau's
Вслед за построением кривой Безье, следующей важной задачей будет нахождение точки p(u) на кривой по заданному u. Простой вариант - развернуть описание кривой в полную форму f(u) = ( f(u), g(u), h(u) ) (см. Пример) и подставлять отдельные значения u в это уравнение, чтобы получать f(u). Хот способ найден, но он не является численно стойким (т.е. в процессе вычисления многочленов могут возникать числовые ошибки).
Далее мы запишем номера [number] контрольных точек. То есть, контрольные точки - это 00 для p0, 01 для p1, ..., 0i для pi, ..., 0n для pn. Нули (0) в этих номерах обозначают начальную или 0-ю итерацию. Позже вместо нуля будет 1, 2, 3, и так далее.
Принцип алгоритма de Casteljau's в таком выборе точки C на отрезке AB, чтобы отношение расстояния между A и C к расстоянию между A и B было равно, скажем, u. Найдем способ определить точку C.
Вектор от A до B равен B - A. Так как u - это коэффициент в пределах от 0 до 1, точка C находится в u(B - A). Вводя в рассмотрение положение точки A, получаем C равно A + u(B - A) = (1 - u)A + uB. Таким образом, для данного u, (1 - u)A + uB - это точка C между A и B, причем отношение расстояний между C и A и между A и B равно u.
Смысл алгоритма de Casteljau's таков. Допустим, надо найти p(u), где u в пределах [0,1]. Начиная с первой ломаной, 00-01-02-03...-0n, на каждом сегменте 0i ... 0(i+1) по вышеуказанной формуле находим точки 1i, такие, чтобы отношение расстояний между 0i и 1i и между 0i и 0(i+1) было равно u. В итоге получим n точек 10, 11, 12, ...., 1(n-1). Они образуют новую ломаную из n - 1 сегментов.
Я тут написал прогу на Delphi, строит кривые Безье по этому алгоритму. Очень просто. Могу дать исходники 8-). (прим. перев.)
На рисунке выше, u равно 0.4. 10 лежит на отрезке между 00 и 01, 11 - между 01 и 02, ..., а 14 - между 04 и 05. Эти новые точки обозначены синим цветом.
Теперь новые точки обозначены 1i. Проделывая эту операцию с новой кривой, затем с полученной и так далее, получим в итоге одну точку. De Casteljau докаазал, что это - точка p(u) на кривой, соответствующая u.
На рисунке выше показано нахождение точки на кривой, для u=0.4 - это точка 50.
Это - геометрическое представление алгоритма de Casteljau, одно из самых красивых в разработке кривых.
Вычисления
На рисунке показана схема нахождения точки на кривой Безье по алгоритму de Casteljau.
Вход (Input): массив p[0:n] из n+1 точек и действительное число u Выход (Output): точка на кривой, p(u) Используется: массив точек q[0:n] for i := 0 to n do
q[i] := p[i]; // сохраняем введенное
for k := 1 to n do
for i := 0 to n - k do
q[i] := (1 - u)q[i] + uq[i + 1];
return q[0];
Рекурсивное Представление
Вышеизложенные вычисления можно провести и по-другому, с помощью рекурсии. Пусть P0,j будет Pj для j = 0, 1, ..., n. То есть, P0,j - это j-й элемент в 0 столбце. Элемент j в столбце i находим так:
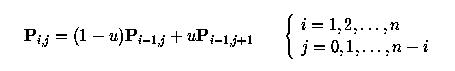
Говоря точнее, элемент Pi,j - это сумма (1-u)Pi-1,j (сверху слева) и uPi-1,j+1 (снизу слева). Конечный результат (т.e. точка на кривой) - это Pn,0. Исходя из этого, можно сразу составить такую рекурсивную процедуру:
function deCasteljau(i,j) begin
if i = 0 then
return P0,j
else
return (1-u)* deCasteljau(i-1,j) + u* deCasteljau(i-1,j+1)
end
Выглядит она простой и короткой; тем не менее, она очень неэффективна. И вот почему.
Блин, не хочу я вам[SSN], объяснять, почему она неэффективна. - (прим. перев.)
We start with a call to deCasteljau(n,0) for computing Pn,0. The else part splits this call into two more calls, deCasteljau(n-1,0) for computing Pn-1,0 and deCasteljau(n-1,1) for computing Pn-1,1.
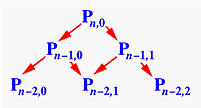
Consider the call to deCasteljau(n-1,0). It splits into two more calls, deCasteljau(n-2,0) for computing Pn-2,0 and deCasteljau(n-2,1) for computing Pn-2,1. The call to deCasteljau(n-1,1) splits into two calls, deCasteljau(n-2,1) for computing Pn-2,1 and deCasteljau(n-2,2) for computing Pn-2,2. Thus, deCasteljau(n-2,1) is called twice. If we keep expanding these function calls, we should discover that almost all function calls for computing Pi,j are repeated, not once but many many times. How bad is this? In fact, the above computation scheme is very similar to the following way of computing the n-th Fibonacci number:
Тут процедура сравнивается с процедурой вычисления чисел Фибоначи - прим. перев.:
function Fibonacci(n) begin
if n = 0 or n = 1 then
return 1
else
return Fibonacci (n-1) + Fibonacci (n-2)
end
Чтобы найти касательный и нормальный вектора в точке на кривой Безье, нам нужно знать ее производную в этой точке. К счастью, это просто, как два бита переслать.
Кривая Безье, построенная по n + 1 контрольным точкам p0, p1, ..., pn имеет следующее уравнение:
где коэффициент Безье Bn,i(u) рассчитывается по формуле:
Так как контрольные точки постоянны и не зависят от переменной u, вычисление p'(u) сводится к вычислению производных коэффициентов Безье. После алгебраических преобразований имеем такой результат для B'n,i(u):
Затем, вычисляя производную кривой p(u), получим:
Пусть q0 = n(p1 - p0), q1 = n(p2 - p1), q2 = n(p3 - p2), ..., qn-1 = n(pn - pn-1). Вышеизложенное уравнение уменьшается до
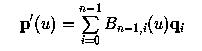
Таким образом, производная p(u) - это кривая Безье n - 1 пстепени, построенная по n контрольным точкам n(p1 - p0), n(p2 - p1), n(p3 - p2), ..., n(pn - pn-1). Эта производная кривая обычно называется годографом исходной кривой Безье. Заметьте, что pi+1 - pi - это вектор от pi до pi+1 и n(pi+1 - pi) в n раз длиннее этого вектора. Имея в наличии контрольные точки кривой, можно легко получить контрольные точки ее производной. Рисунок слева показывает кривую Безье 7 степени, а справа - ее производную, т.е. кривую Безье 6 степени.
