Кривые b-spline: Важные Свойства

У кривых B-spline много свойств, схожих с кривыми Безье, так как они являются обощением последних. Более того, кривые B-spline имеют больше желаемых свойств, чем кривые Безье. На этой странице перечислено большинство важных свойств B-spline. Мы рассмотрим только фиксированные кривые B-spline.

В дальнейшем будем считать, что кривая B-spline p(u) степени p определяется n + 1 контрольными точками, узловым вектором U = { u₀, u₁, ...., u_m } с первыми p+1 и последними p+1 "склеенными" узлами (т.e. u₀ = u₁ = ... = u_p и u_m-p = u_m-p+1 = ... = u_m).

1. Кривая B-spline p(u) является кусочной кривой, каждый компонент которой - кривая степени p. Как упоминалось на предыдущей странице, p(u) можно представить как объединение отрезков кривых, построенных на каждом узловом интервале. На рисунке ниже, при n = 10, m = 14 и p = 3, четыре первых и четыре последних узла фиксированы, а 7 средних узлов равномерно распределены. Всего 8 узловых интервалов, каждый из которых соответствует отрезку кривой. Делящие точки - это p(u_i). На рисунке слева эти точки показаны треугольниками.

Это полезное свойство дает нам возможность проектировать кривые очень сложных форм, используя многочлены низких степеней. Например, ниже правый рисунок показывает кривую Безье с тем же набором контрольных точек. Кривая не очень-то следует за контрольной ломаной, а ее степень равна 10!

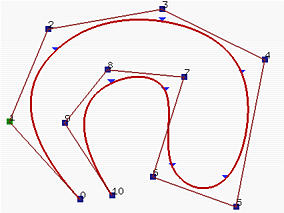
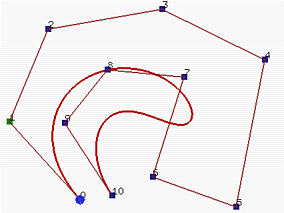
В общем случае, чем меньше степень, тем сильнее кривая B-spline приближается к ее контрольной ломаной. На рисунках далее показаны кривые с одной и той же контрольной ломаной, их узлы фиксированы и равномерно распределены. На первом рисунке кривая 7 степени, на среднем - 5, а на правом - 3. Таким образом, при увеличении степени полученный B-spline приближается к его контрольной ломаной.

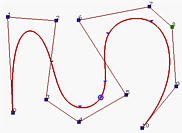
2. Равенство m = n + p + 1 должно выполняться Так как для каждой контрольной точки нужна базисная функция и количество базисных функций удовлетворяет условию m = n + p + 1.

3. Фиксированный кривая B-spline p(u) проходит через две крайние контр. точки p₀ и p_n Заметьте, что базисная функция N_0,p(u) - это коэффициент контрольной точки p₀ и не равна нулю на [u₀,u_p+1). Так как u₀ = u₁ = ... = u_p = 0 для фиксированной кривой B-spline, N_0,0(u), N_1,0(u), ...., N_p-1,0(u) равны нулю и только N_p,0(u) не равно нулю (вспомните из треугольной формы расчета). Следовательно, когда u = 0, N_0,p(0) равно 1 и p(0) = p₀. Аналогичные рассуждения могут показать, что p(1) = p_n

4. Свойство Сильного Ограничивающего Многоугольника [Strong Convex Hull Property]: кривая B-spline содержится в ограничивающем многоугольнике ее контрольной ломаной. Говоря точнее, если u лежит на узловом интервале [u_i,u_i+1), то p(u) находится в ограничивающем многоугольнике контр. точек p_i-p, p_i-p+1, ..., p_i Если u лежит на узловом интервале [u_i, u_i+1), есть только p+1 базисных функций (i.e., N_i,p(u), ... , N_i-p+1,p(u), N_i-p,p(u) ), ненулевых на этом узловом интервале. Так как N_k,p(u) - это коэффициент контр. точки p_k, только p+1 контр. точек p_i, p_i-1, p_i-2, .., p_i-p имеют ненулевые коэффициенты. Так как на этом узловом интервале базисные функции не равны нулю и в сумме составляют 1, их точка "среднего взвешенного", p(u), должна находится внутри ограничивающего многоугольника контр. точек p_i, p_i-1, p_i-2, .., p_i-p. Значение слова "сильный" в том, что кроме того, что p(u) лежит внутри ограничивающего многоугольника всех точек, она находится еще и внутри гораздо меньшего многоугольника.

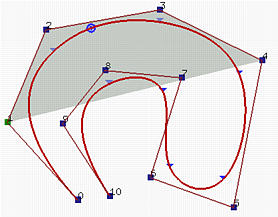
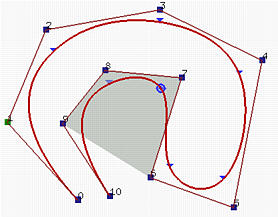
Две показаные выше кривые B-spline имеют 11 контр. точек (т.e. n = 10), 3 степени (т.e. p=3) и 15 узлов (m = 14), четыре первых и четыре последних узла фиксированы. Таким образом, количество узловых интервалов равно количеству отрезков кривых. Узловой вектор - это

u0	u1	u2	u3	u4	u5	u6	u7	u8	u9	u10	u11	u12	u13	u14
0	0	0	0	0.12	0.25	0.37	0.5	0.62	0.75	0.87	1	1	1	1

На рисунке слева u лежит на узловом интервале [u₄, u₅) = [0.12,0.25), а соответствующая точка (т.e. p(u)) - на втором отрезке кривой. Таким образом, p+1 = 4 базисных функции - ненулевые на этом интервале (т.e. N_4,3(u), N_3,3(u), N_2,3(u) и N_1,3(u) ), а соответствующие контрольные точки - это p₄, p₃, p₂ и p₁. Темная область - это огранич. многоугольник для этих четырех точек. Ясно, что p(u) лежит в этом многоугольнике.

Кривая B-spline на правом рисунке описывается так же. Но в данном случае u на интервале [u₉, u₁₀) = [0.75,0.87) и ненулевые функции - это N_9,3(u), N_8,3(u), N_7,3(u) и N_6,3(u). Соответствующие контрольные точки - p₉, p₈, p₇ и p₆.

Следовательно, когда u движется от 0 к 1 и переходит узел, базисные функции становятся нулями, а новая базисная функция становится эффективной. В результате одна контрольная точка, коэффициент которой становится равным 0, выходит за пределы огранич. многоугольника и заменяется новой контрольной точкой, коэффициент которой не равен нулю.

5. Схема Локального Изменения [Local Modification Scheme] : имзенение положения контрольной точки p_i влияет только на кривую p(u) на интервале [u_i, u_i+p+1) Это следует из другого важного свойства базисных функций B-spline. Вспомним, что N_i,p(u) не равно нулю на интервале [u_i, u_i+p+1). Если u не на этом интервале, то N_i,p(u)p_i не влияет на вычисление p(u), так как N_i,p(u) равно нулю. С другой стороны, если u находится в указанном интервале, N_i,p(u) не равно нулю. Если p_i изменяет положение, N_i,p(u)p_i тоже изменяется и, следовательно, изменяется и p(u).

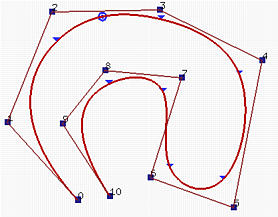
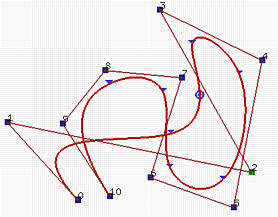
Вышеуказанные кривые B-spline имеют те же параметры, что и в предыдущем примере. Переместим контр. точку p₂. Коэффициент этой контр. точки равен N_2,3(u), а интервал, на котором этот коэффициент не равен нулю - это [u₂, u₂₊₃₊₁) = [u₂, u₆) = [0,0.37). Так как u₂ = u₃ = 0, то только три отрезка, соответствующих [u₃, u₄) (область первого отрезка кривой), [u₄, u₅) (область второго отрезка кривой) и [u₅, u₆) (область третьего отрезка кривой) будут затронуты. Рисунок справа показывает результат перемещения p₂ в правый нижний угол. Как видите, только первый, второй и третий отрезки кривой изменили форму, а все остальные остались неизменными.

Эта схема локального изменения очень важна для проектирования кривых, потому что можно изменять кривую локально, не изменяя форму кривой в целом. Более того, если нужна точная настройка кривой, можно добавить больше узлов (соответственно, и контр. точек) так, чтобы зона изменения была очень малой областью. Мы поговорим об добавлении узлов позже.

6. p(u) имеет непрерывность C^p-k в узле множественности k Если u - это не узел, то p(u) находится в середине отрезка кривой степени p, и поэтому бесконечно дифференцируема. Если u - это узел на ненулевой области определения N_i,p(u), так как последняя только C^p-k-непрерывна, то и p(u) тоже.

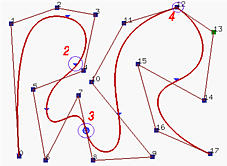
Вышеуказанная кривая имеет 18 контр. точек (т.e. n = 17), степень, равную 4, и следующий фиксированный узловой вектор

от u0 до u4	u5	u6 и u7	u8	от u9 до u11	u12	от u13 до u16	u17	от u18 до u22
0	0.125	0.25	0.375	0.5	0.625	0.75	0.875	1

Таким образом, u₆ является двойным узлом, u₉ тройным узлом, а u₁₃ - четверным. Следовательно, p(u) имеет непрерывность C⁴ в любой точке, не являющейся узлом, непрерывность C³ во всех простых узлах, непрерывность C² в u₆, непрерывность C¹ в u₉, непрерывность C⁰ в u₁₃.

Все точки на кривой, соответствующие узлам, обозначены маленькими треугольниками, соответствующие множественным узлам - окружностями с числом, указывающим их множественность. Очень сложно зрительно показать разницу между непрерывностями C⁴, C ³ и даже C². Для случая C¹ соответствующая точка лежит на сегменте, тогда как в случае C⁰ кривая проходит через контрольную точку. Мы еще вернемся к этому позднее, при обсуждении изменения узлов.

7. Свойство Уменьшения Изменчивости [Variation Diminishing Property] : Свойство уменьшения изменчивости также подходит и для кривых B-spline. Если кривая на плоскости (соотв., в пространстве), это значит, что не существует прямой (соотв., плоскости), пересекающей кривую B-spline больше раз, чем ее контрольную ломаную.

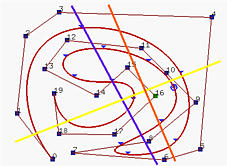
На рисунке выше синяя линия пересекает как контрольную ломаную, так и кривую B-spline 6 раз, тогда как желтая линия пересекает их по 5 раз. Однако оранжевая линия пересекает контрольную ломаную 6 раз, а кривую 4 раза.

8. Кривые Безье - это Особый Случай Кривых B-spline Если n = p (т.e. степень кривой B-spline равна n, количество контрольных точек минус 1) и есть 2(p + 1) = 2(n + 1) узлов, p + 1 из которых фиксированы на концах, этот B-spline сводится к кривой Безье.

9. Инвариантность При Подобных Преобразованиях Это свойство также подходит к кривым B-spline. Если к кривой B-spline применяются преобразования подобия, то тот же результат можно получить, применив те же преобразования к контрольным точкам, а потом по ним построить кривую.