Параметрические Кривые: Обзор
Каждая грань ограничена ребрами, которые могут быть отрезками прямых или кривых, а грань сама по себе - частью поверхности (т.e. элемента поверхности). В этом разделе мы поговорим об основных понятиях криволинейных отрезков в параметрической форме.
параметрическая кривая в пространстве имеет следующий вид:
f: [0,1] -> ( f(u), g(u), h(u) ),
где f(), g() и h() - это три функции с дробными значениями, сопоставляющие дробному числу u на отрезке [0,1] точку в пространстве. Областью значений этих функций и векторной функции f() не обязательно будет [0,1]. Это может быть любой закрытый интервал; но, для простоты, ограничимся отрезком [0,1]. Таким образом, каждому u на отрезке [0,1], соответствует точка ( f(u), g(u), h(u) ) в пространстве.
Здесь и далее, функции f(), g() и h() - всегда многочлены.
Заметьте, что если функцию h() удалить из определения f(), у f() остается две составляющих и получается кривая на плоскости.
Примеры
Векторное уравнение прямой такое: B+td, где B - это базовая точка, а d - это направляющий вектор. Таким образом, если f() определяется как
f(u) = b1 + ud1 g(u) = b2 + ud2 h(u) = b3 + ud3,
где B = < b1, b2, b3 > и d = < d1, d2, d3 >, и f() - это параметрическая кривая, сопоставляющая [0,1] с отрезком прямой от B до B+d, включительно.
Окружность имеет следующее уравнение не в виде многочлена:
x(u) = rcos(2*PI*u) + p y(u) = rsin(2*PI*u) + q
Ее центр - (p, q), радиус r. Так как параметр u в пределах [0,1], значение 2*PI*u находится в пределах [0,2*PI] (т.e. от 0 до 360 градусов).
Исключим u. Сначала изменим уравнения. Для удобства выбросим (u) из x(u) и y(u).
x - p = rcos(2*PI*u) y - q = rsin(2*PI*u)
Затем, возводя оба уравнения в квадрат и складывая, получаем:
(x - p)2 + (y - q)2 = r2
Таким образом, эта параметрическая форма описывает окружность.
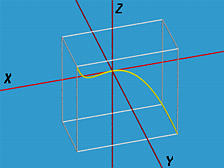
Кубическая кривая в пространстве имеет следующий вид:
f(u) = u g(u) = u2 h(u) = u3
Следующий рисунок показывает эту кривую в пределах [-1,1]. Она содержится в прямоугольном параллелепипеде между точками ( -1, 0, -1 ) и (1, 1, 1)
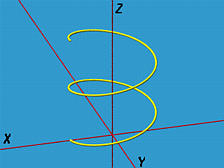
Круговая спираль описывается так:
f(u) = ( acos(u), asin(u), bu )
Рисунок ниже показывает эту кривую на отрезке [0, 4*PI]. Начальная точка - (a, 0, 0), а конечная - (a, 0, b). Заметьте, что кривая лежит на цилиндре радиуса a с центральной осью z.
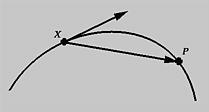
Касательный Вектор и Касательная
Здесь точка X фиксированная, а P- движущаяся. По мере приближения P к X, вектор от X к P приближается к касательному вектору к кривой в точке X. Прямая, на которой этот вектор лежит - это касательная.
Вычислить касателный вектор легко. Производная кривой f(u) имеет вид:
f'(u) = ( f'(u), g'(u), h'(u) ),
где f'(u) = df/du, g'(u) = dg/du, а h'(u) = dh/du.
Вообще, длина кас. вектора f'(u) не равна 1, нужна нормализация. То есть, единичный вектор при значении параметра u, или в точке f(u), равен
f'(u) / | f'(u) | ,
где | x | - это длина (модуль) x. Касательная к f(u) - это либо
f(u) + tf'(u),
или, если использовать единичный вектор,
f(u) + t(f'(u)/|f'(u)|) ,
где t это параметр. Заметьте, в этом случае u фиксировано.