Глава 1

33. 

    Постройте окружность, которая касается сторон данного угла, причем одной из них — в данной на ней точке F.

34. Постройте окружность, которая проходит через данную точку A и касается данной окружности в данной на ней точке F.

35. Постройте окружность, которая касается данной прямой l и данной окружности в данной на ней точке T.

36. Через точку пересечения двух данных окружностей проведите прямую так, чтобы часть ее, расположенная внутри окружностей, равнялась данному отрезку a.

37. Дан треугольник ABC, AB = c, BC = a, CA = b. Постройте окружности с центрами соответственно в точках A, B, C так, чтобы они попарно касались друг друга внешним образом.

Центральные и вписанные углы

Скачено с Образовательного портала www.adu.by

24

Глава 1

Вписанные и описанные многоугольники

25

§ 2. Центральные и вписанные углы

1 . Центральные углы. Градусная мера дуги окружности. В данном параграфе изучим понятия центрального и вписанного углов.

О п р е д е л е н и е. Центральным углом окружности назы вается угол с вершиной в центре этой окружности.

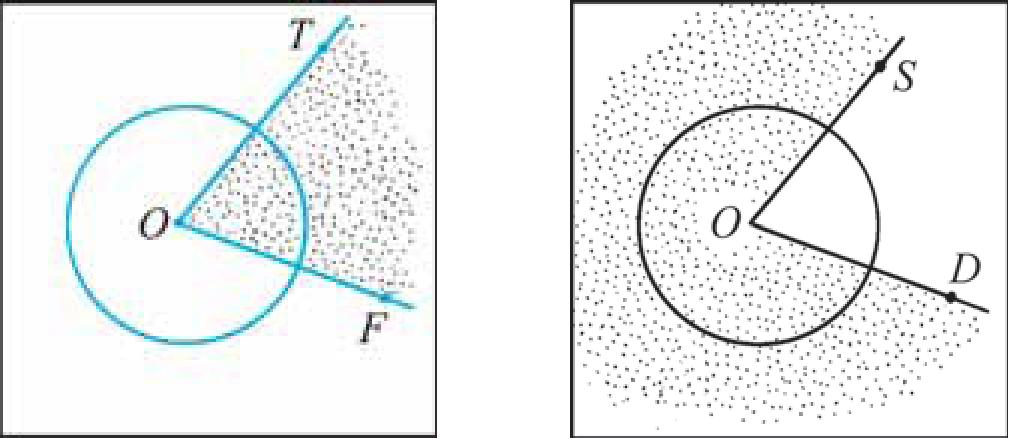
а) б)

Рис. 18

Например, на рисунке 18, а изображен центральный угол TOF, который меньше развернутого угла, а на рисунке 18, б — центральный угол DOS — больший развернутого угла.

Любые две различные точки A и В окружности служат концами двух дуг. Для различия этих дуг на каждой из них отмечается некоторая промежуточная точка. Например, если на дугах отмечены точки F и T, то в этом случае дуги обозначаются ∪ATB и ∪AFB и данная запись читается так: «дуга ATB и дуга AFB» (рис. 19, а). Если понятно, о какой из двух дуг идет речь, употребляется также обозначение ∪AB.

Дуга AB окружности называется полуокружностью, если ее концы служат концами диаметра этой окружности.

Например, на рисунке 19, б изображены полуокружности ALB и AC B .

Пусть A и B не являются диаметрально противолежащими точ­ками окружности с центром в точке O. Тогда лучи OA и OB служат сторонами двух центральных углов, один из которых меньше, а другой больше развернутого угла (рис. 20, а).

Дуга AB окружности ω (O; R) и центральный угол AO B , внутри которого лежит эта дуга, называются соответствующими.

Если дуга окружности лежит внутри соответствующего ей цен­трального угла, который меньше развернутого угла, то говорят, что эта дуга меньше полуокружности.

Если дуга окружности лежит внутри соответствующего ей цен­трального угла, который больше развернутого угла, то говорят, что дуга больше полуокружности.

а) б) в)

Рис. 20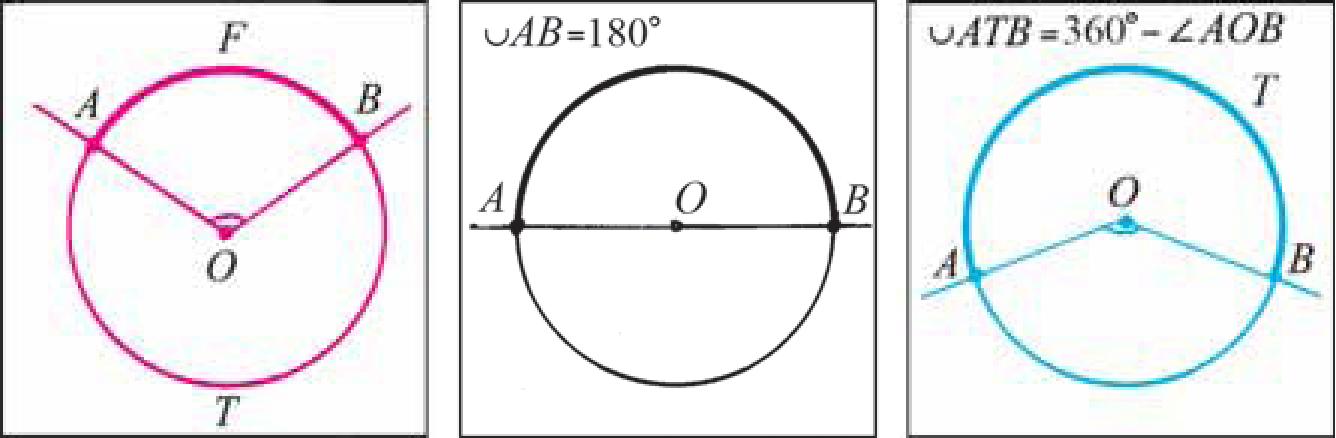

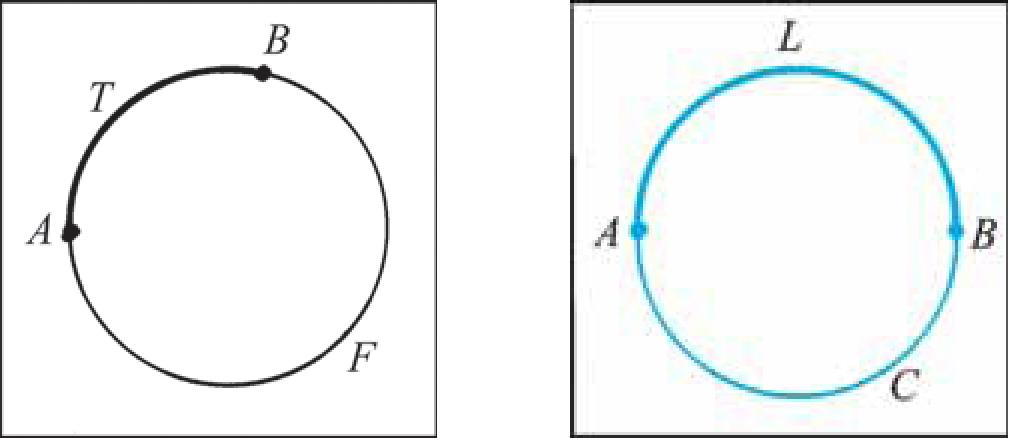
Например, на рисунке 20, а изображены дуга AFB, которая меньше полуокружности, и дуга ATB — больше полуокружности.

а) б)

Рис. 19

Скачено с Образовательного

Для сравнения дуг окружности вводится понятие градусной меры дуги окружности.

Определение. Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла.

Градусная мера дуги АВ, как и сама дуга, обозначается yjAB.

Таким образом, если дуга АВ окружности меньше полуокружности, а Z АОВ — соответствующий ей центральный угол, то yjAB = Z АОВ (рис. 20, а).

Если дуга АВ является полуокружностью, то ее градусная мера равна 180° (рис. 20, б).

портала www.adu.by

26